Класс точности измерительного прибора это величина систематической ошибки, вносимой данным прибором при измерении, выраженная в процентах от шкалы прибора.

Рассмотрим пример. Амперметр имеет предел измерений 100А, цена деления шкалы 1А, класс точности «2». Систематическая ошибка, вносимая при измерении, вычисляется так: 2х0,01х100=2 (А).

Представим, что мы провели измерение силы тока и получили результат (действительное значение) 58 А. Правильная запись результата измерения выглядит так: 58±2 (А) и означает, что истинное значение силы тока лежит в интервале от 56 до 60 А. Ничего более точного мы не имеем права утверждать, поскольку точность в нашем случае ограничена классом точности использованного прибора.

Ошибки, вызванные воздействием разнообразных мешающих факторов, называются случайными. Воздействие этих факторов неодинаково в каждом измерении, вследствие чего мы можем получать различные действительные значения. При этом, если мы берем более точный измерительный прибор, роль случайных ошибок сказывается в большей степени. Если мы будем измерять диаметр заготовки линейкой, а, скажем ее истинный размер 20,20002.… мм, то всякий раз, прикладывая линейку, мы будем получать один и тот же результат 20 мм. Если используем для измерений микрометр, то будем получать значения, например, 20,18; 20,21 и так далее. Причина в том, что начинают сказываться различные случайные факторы. Пылинка села, на деталь попало масло, у микрометра имеется люфт и т.п. Это воздействие случайных причин приводит к тому, что мы получаем разброс значений. Повысить точность измерений, т.е. приблизиться к истинному значению возможно путем многократных измерений и статистической обработки их результатов.

Статистическая обработка результатов состоит в вычислении среднего арифметического значения 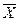и среднеквадратичной ошибки 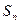по формулам …

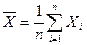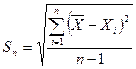
Результат измерений и вычислений принято представлять в виде:

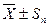
Средняя квадратичная ошибка дает информацию об интервале, внутри которого лежит истинное значение с определенной надежностью. Этот интервал называется «доверительный интервал». В математической теории ошибок показано, что доверительному интервалу 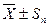соответствует надежность 68%. Если мы хотим указать истинное значение с большей точностью, мы должны увеличить доверительный интервал. Так доверительному интервалу 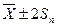соответствует надежность 95%, а доверительному интервалу 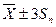соответствует надежность 99,5%. В каком же интервале лежит истинное значение с надежностью 100%, т.е.наверняка? Ответ очевиден: внутри интервала 0¸¥.

Разберем пример. При измерении диаметра заготовки штангенциркулем мы получили действительные значения 18,7; 18,8 и 21,0 мм. Вычислим среднее арифметическое значение 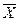и среднеквадратичную ошибку .

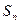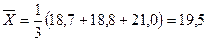
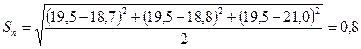
Правильная запись результата измерений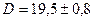

Смысл этой записи следующий: истинное значение диаметра лежит внутри интервала 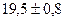(мм) с надежностью 68%

Третий вид ошибок, с которыми можно столкнуться при измерении, грубая ошибка оператора – промах.

Эта ошибка связана с невнимательностью оператора, самые распространенные случаи ее возникновения – ошибка в запятой при записи результата, вписывание результата не в ту графу и считывание результата не с той шкалы.

16. Необходимое количество измерений при контроле сварных соединений.

Если мы в результате измерений в одной и той же точке получаем отличающиеся друг от друга значения, это означает, что случайная ошибка велика. Если в процессе измерения мы получаем практически одно и тоже значение (вспомните измерение диаметра детали линейкой), в этом случае случайная ошибка несущественна, поэтому достаточно измерить один раз. Вывод такой. Если мы пользуемся точным средством измерений, и случайная ошибка является преобладающей, тогда многократное измерение ведет уменьшению случайной ошибки и повышению точности измерения. Если преобладающей является систематическая ошибка, то многократное измерение не дает выигрыша в точности. Тогда достаточно выполнить измерение однократно. Например, при измерении шаблоном сварщика достаточно провести измерение один раз. Если обе ошибки сопоставимы по величине, тогда в качестве погрешности измерений, указываемой в отчете об измерениях, указывают суммарную ошибку.

При записи последовательных результатов измерения одного и того же размера в одной и той же точке одним и тем же прибором нужно указывать одинаковое количество знаков после запятой для каждого измерения. Нельзя, например, записать 18,7; 18,78 и 21 мм. Надо записать соответственно 18,7; 18,8 и 21,0 мм. То же относится к среднему арифметическому и ошибке измерения. Правильная запись 19,5±0,8. Запись 19,5±0,82 или 20±0,82 неправильная.

17. Допускаемая погрешность измерения.

Повторим определение термина «измерение» из п.14.Измерением называется определение численного значения физической величины опытным путем с использованием специальных технических средств в установленных единицах измерения.

Рассмотрев в п.15 понятие «ошибки измерения», мы можем теперь утверждать, что, выполняя измерение, т.е. стараясь определить истинный размер объекта контроля, мы на самом деле с большей или меньшей надежностью определяем интервал, в котором находится истинный размер. Ширина этого интервала, равная удвоенной суммарной ошибке измерения (систематической плюс случайной), как мы себе уяснили, зависит от точности средства измерения и количества выполненных измерений.