Графический анализ функции правдоподобия
Одно из достоинств использования функции правдоподобия при анализе данных состоит в том, что часто удается найти графический вид этой функции и тем самым наглядно представить полученный результат. Этот метод неудобен, если имеется три или большее число параметров, оценки которых независимы.
Допустим, что имеется один независимый параметр . Изобразив графически функцию l() или фенкцию L()=ln[l()], можно сразу же найти значение которому соответствует «наивысшей» точке кривой. Это избавляет нас от трудоемких расчетов в тех случаях, когда соответствующее максимуму значение не может быть найдено аналитически и приходится прибегать к итерации. Кроме того, используя график, можно тотчас указать доверительный интервал или ошибку полученной оценки, проведя на графике соответствующую линию.
В том случае, когда имеется два параметра и функция правдоподобия представляет собой поверхность, контуры которой можно изобразить на плоскости (). Обычно, когда максимум располагается внутри области, контурами равного правдоподобия являются замкнутые кривые. В этом случае двумерным доверительным интервалом служит площадь, охватываемая контуром.
Случай непрерывного параметра
Пусть имеется нормальное распределение с единственной дисперсией и неизвестным параметром N(,1). Функция правдоподобия m получится из выборки объема n, имеет вид
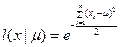
Она представляет собой такую же колоколообразную кривую, что и плотность вероятности с центром в точке =x. В данном случае удобнее иметь дело с логарифмической функцией правдоподобия
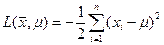
К выражению можно добавить любую const не содержащую . Если в качестве такой const взять
 ,
,
то функцию
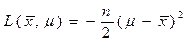 ,
,
представляющую собой параболу, ширина которой растет пропорционально 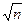 , а максимум, равный нулю, расположен при =x. Если n=1, то
, а максимум, равный нулю, расположен при =x. Если n=1, то
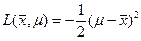
Изобразим функцию:
 |
Подобный график лежит в основе анализа большого класса функций правдоподобия, которые зависят от одного параметра и обладают следующими свойствами:
1. L() – непрерывны
2. L() – имеют единственный максимум в интересующей нас области.
Приведенная выше логарифмическая функция правдоподобия имеет максимум при =x.
Согласно свойствам нормального распределения, выражению
 соответствует доверительная вероятность, равная 68,3%. Аналогично, отрезок прямой, проведенной на уровне L=-2, соответствует 95% доверительному интервалу.
соответствует доверительная вероятность, равная 68,3%. Аналогично, отрезок прямой, проведенной на уровне L=-2, соответствует 95% доверительному интервалу.
Б) случай неизвестной дисперсии: если в рассмотренном примере дисперсия неизвестна, то возникает двухпараметрическая задача:
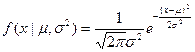
Следовательно:
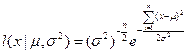
логарифмическая функция правдоподобия
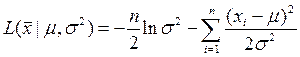
Необходимо найти пару значений 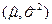 , которые с наибольшей вероятностью приводили бы к наблюдаемым значениям
, которые с наибольшей вероятностью приводили бы к наблюдаемым значениям  . Для этого нужно решить совместно два уравнения:
. Для этого нужно решить совместно два уравнения:
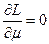 и
и 
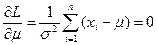 ,
,
откуда 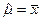
Далее 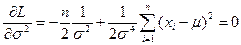 ,
,
Откуда 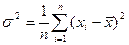
Видно, что оказывается смещенной оценкой дисперсии т.к.
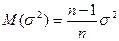
Дата добавления: 2018-06-28; просмотров: 1151;
