Статистические параметры
- Параметры распределения.
Параметрами распределения вероятностей называется набор чисел, значения которых полностью определяют это распределение как конкретный элемент некоторого семейства вероятностных распределений.
Пример. Параметрами нормального распределения вероятностей на числовой прямой обычно выступает его математическое ожидание (пусть это будет 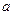 ) и дисперсия (пусть это будет
) и дисперсия (пусть это будет 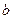 ). В этом случае нормальная плотность как функция аргумента
). В этом случае нормальная плотность как функция аргумента 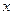 , изменяющегося от –
, изменяющегося от – 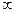 до +
до + 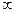 , зависит от
, зависит от 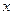 и параметров (
и параметров ( 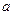 ,
, 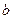 ) следующим образом:
) следующим образом:
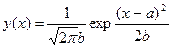
В дальнейшем параметр (или всю их совокупность) будем обозначать одной буквой, скажем  . Если параметр один, то
. Если параметр один, то  – число. Если параметров несколько (r), то
– число. Если параметров несколько (r), то 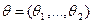 –их совокупность. Обычно параметризацию семейства распределений вводят так, чтобы между значениями параметров и элементами семейства устанавливалось взаимно-однозначное соответствие, т. е. Чтобы разным наборам
–их совокупность. Обычно параметризацию семейства распределений вводят так, чтобы между значениями параметров и элементами семейства устанавливалось взаимно-однозначное соответствие, т. е. Чтобы разным наборам 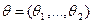 и
и 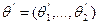 соответствовали разные распределения. В остальном выбор параметров (способов параметризации) диктуется конкретными обстоятельствами. Например, для нормального распределения на прямой возможна и параметризация с помощью параметров
соответствовали разные распределения. В остальном выбор параметров (способов параметризации) диктуется конкретными обстоятельствами. Например, для нормального распределения на прямой возможна и параметризация с помощью параметров 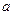 и
и 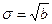 .
.
- Оценки параметров.
Любые характеристики распределения вероятностей могут быть выражены через его параметры. Поэтому одна из основных задач математической статистики—по наблюдениям над независимыми реализациями случайной величины (т. е. выборке) сделать выводы о параметрах распределения, например, указать их приближенные значения. Вместо словосочетания “приближенное значение” в статистике используется термин “оценка”. Т. е., чтобы указать приближенные значения параметров, нужно их оценить, т. е. Указать их оценки.
Если 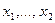 -совокупность независимых одинаково распределенных случайных величин (выборка), распределение вероятностей которых зависит от неизвестного параметра
-совокупность независимых одинаково распределенных случайных величин (выборка), распределение вероятностей которых зависит от неизвестного параметра  , то в качестве оценки могут выступать функции от аргументов
, то в качестве оценки могут выступать функции от аргументов 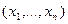 , т. е.
, т. е. 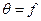
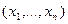 .
.
- Оценивание параметров распределения по выборке.
Методы оценивания делят на две группы:
а) оценивание параметров по конечной выборке.
б) оценивание по неограниченно растущей выборке.
С практической точки зрения группа методов б) важнее, т. к. интуитивно понятно, что для получения надежных выводов о параметрах надо иметь достаточно информации, т. е. Проделать большое число экспериментов. Кроме того, с теоретической точки группе б) подход проще, так как при больших n исчезают многие проблемы, относящиеся к конечным выборкам.
Основой для выводов в этом случае служит закон 3 больших чисел – при больших n значения выборочных характеристик распределения приближаются к неизвестным чем теоретическим значениям этих характеристик.
Теорема Чебышева. Пусть 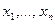 - независимые одинаково распределенные случайные величины, имеющие математическое ожидание и дисперсию. Общее значение математического ожидания этих величин обозначим через
- независимые одинаково распределенные случайные величины, имеющие математическое ожидание и дисперсию. Общее значение математического ожидания этих величин обозначим через 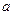 .
.
Тогда, для любого 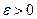 при
при 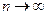
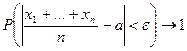
В статистика среднее арифметическое величин 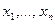 обозначают
обозначают 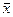 . Так что кратко теорему Чебышева можно записать так:
. Так что кратко теорему Чебышева можно записать так: 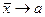 .
.
Если посмотреть с этих позиций на теорему Чебышева, то видно, что она дает способ оценки по выборке теоретического значения математического ожидания, - его оценкой является среднее значение наблюдений: 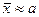 .
.
Получим аналогичный результат для дисперсии распределения.
- Оценка дисперсии распределения.
Пусть 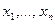 - совокупность независимых реализаций случайной величины
- совокупность независимых реализаций случайной величины 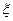 . Согласно закону больших чисел, для получения приближенного значения дисперсии
. Согласно закону больших чисел, для получения приближенного значения дисперсии  надо в определении дисперсии заменить теоретическую функцию распределения
надо в определении дисперсии заменить теоретическую функцию распределения 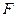 на её выборочный аналог
на её выборочный аналог 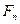 . Иначе говоря, требуется заменить операцию математического ожидания
. Иначе говоря, требуется заменить операцию математического ожидания 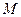 усреднением по выборке. Сначала сделаем это по отношению к
усреднением по выборке. Сначала сделаем это по отношению к 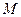 , стоящему внутри скобок: вместо
, стоящему внутри скобок: вместо 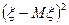 получим совокупность
получим совокупность
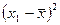 ,
, 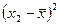 ,…,
,…, 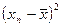
Остается применить операцию усреднения вместо внешнего символа 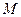 : получим приближенное выражение для дисперсии:
: получим приближенное выражение для дисперсии: 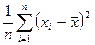
Докажем закон больших чисел для дисперсии.
Надо доказать, что при 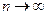
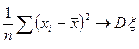
Преобразуем 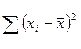 следующим образом:
следующим образом:
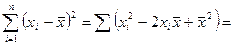
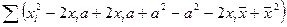 =
=
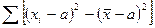 =
= 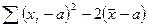
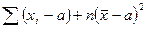 =
= 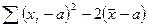
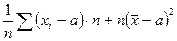 =
= 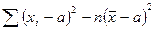
Так как 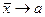 , то
, то 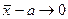 при
при 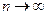 .
.
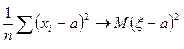 при
при 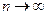 , т. е. Сходится к
, т. е. Сходится к 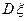 . Выражение
. Выражение 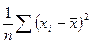 называется выборочной дисперсией (или дисперсией выборки).
называется выборочной дисперсией (или дисперсией выборки).
Чаще вместо этого используется следующее выражение:

Понятно, что уменьшение n на 1 в знаменателе не сказывается на предельном поведении этого выражения и  при
при 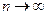 . В то же время
. В то же время 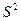 обладает тем свойством, что
обладает тем свойством, что 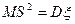 при любом n.
при любом n.
Говорят, что 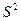 является несмещенной оценкой.
является несмещенной оценкой.
- Метод моментом (на примере нормального распределения).
Пусть 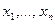 - независимые случайные величины, распределенные по нормальному закону с параметрами
- независимые случайные величины, распределенные по нормальному закону с параметрами 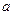 и
и 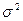 . (по закону N(
. (по закону N( 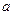 ,
, 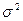 )).
)).
В качестве характеристик распределения будем использовать первый и второй моменты ( 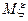 и
и 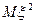 ).
).
Теоретические значения этих характеристик равны 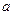 и
и  . приравнивая выборочные моменты к их теоретическим аналогам, получим систему уравнений относительно
. приравнивая выборочные моменты к их теоретическим аналогам, получим систему уравнений относительно 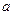 и
и 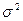 .
.
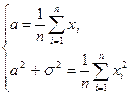
Решение системы, т. е. моментные оценки 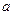 и
и 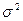 , обозначим как
, обозначим как 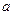 * и
* и 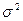 *.
*.

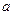 *
* 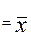

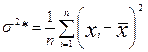
 Заметим, что мы получили бы для
Заметим, что мы получили бы для 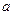 и
и 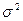 иные выражения, если бы в качестве характеристик распределения взяли бы другие моменты (не первый и второй, как в приведенном случае).
иные выражения, если бы в качестве характеристик распределения взяли бы другие моменты (не первый и второй, как в приведенном случае).
 6. Метод квантилей.
6. Метод квантилей.
 Чтобы использовать метод квантилей, необходимо сначала решить, какими квантилями пользоваться. Для нормальной выборки (и вообще для выборок, в которых параметрами служат сдвиг и масштаб) обычно используют медиану и квартили – верхнюю и нижнюю.
Чтобы использовать метод квантилей, необходимо сначала решить, какими квантилями пользоваться. Для нормальной выборки (и вообще для выборок, в которых параметрами служат сдвиг и масштаб) обычно используют медиану и квартили – верхнюю и нижнюю.
 Случайную величину
Случайную величину 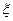 , распределенную по закону N(
, распределенную по закону N( 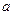 ,
, 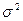 ), можно представить в виде
), можно представить в виде 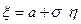 , где
, где 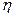 подчиняется закону
подчиняется закону 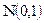 . Для стандартного распределения
. Для стандартного распределения 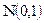 медиана равна 0, а нижняя и верхняя квартили равны
медиана равна 0, а нижняя и верхняя квартили равны 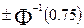 соответственно. Поэтому, для N(
соответственно. Поэтому, для N( 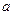 ,
, 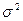 ) медиана равна
) медиана равна 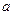 , квартили (верхняя, нижняя) равны
, квартили (верхняя, нижняя) равны 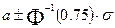 . Видно, что
. Видно, что 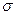 равна половине разности верхней и нижней квартилей распределения, деленной на
равна половине разности верхней и нижней квартилей распределения, деленной на 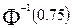 . [
. [ 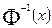 - обратная функция Лапласа].
- обратная функция Лапласа].
 Обозначим через
Обозначим через  медиану выборки
медиану выборки 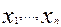 , а через
, а через 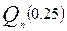 и
и 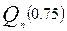 её нижнюю и верхнюю квартили. Приравняв теоретическими характеристиками их выборочные аналоги, получим оценки для
её нижнюю и верхнюю квартили. Приравняв теоретическими характеристиками их выборочные аналоги, получим оценки для 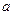 и
и 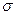 :
:

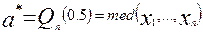 .
.

 .
.
 Свойства оценок.
Свойства оценок.
 Так как для одних и тех же параметров распределения возможны и употребительны разные оценки, то желательно выбирать те из них, которые лучшие или которые обладают желательными свойствами. Пусть
Так как для одних и тех же параметров распределения возможны и употребительны разные оценки, то желательно выбирать те из них, которые лучшие или которые обладают желательными свойствами. Пусть 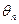 - оценка характеристики распределения
- оценка характеристики распределения  , полученная по выборке объема
, полученная по выборке объема 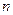 .
.
 Тогда: оценка
Тогда: оценка 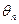 называется состоятельной, если
называется состоятельной, если 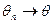 по вероятности, когда
по вероятности, когда 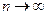 .
.
 оценка
оценка 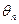 называется несмещенной, если
называется несмещенной, если 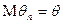 .
.
 1. Эффективность оценок.
1. Эффективность оценок.
 Чаще всего в качестве критерия качества оценки
Чаще всего в качестве критерия качества оценки 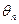 параметра
параметра  выбирают малость величины
выбирают малость величины 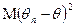 , а наилучшей оценкой считают такую оценку, для которой эта величина минимальна. Более общий подход состоит в том, что вместо величины
, а наилучшей оценкой считают такую оценку, для которой эта величина минимальна. Более общий подход состоит в том, что вместо величины 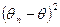 выбирают другую неотрицательную функцию «штрафа»
выбирают другую неотрицательную функцию «штрафа» 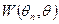 за отклонение
за отклонение 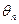 от
от  (иногда говорят, функцию потерь), и наилучшей оценкой считают такую, для которой математической описание величины штрафа
(иногда говорят, функцию потерь), и наилучшей оценкой считают такую, для которой математической описание величины штрафа 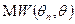 оказывается минимальным.
оказывается минимальным.
 Оценки, для которых минимальна некоторая функция потерь, часто называется оптимальными и эффективными.
Оценки, для которых минимальна некоторая функция потерь, часто называется оптимальными и эффективными.
 Не следует приписывать этим определением какие-либо магические свойства, считая что такие оценки заведомо лучше других. На самом деле оптимальные свойства оценок получены при определенных предположениях, которые на практике могут и не выполняться или выполняться приблизительно: например, среднее арифметическое элементов выборки является «эффективной» оценкой параметра
Не следует приписывать этим определением какие-либо магические свойства, считая что такие оценки заведомо лучше других. На самом деле оптимальные свойства оценок получены при определенных предположениях, которые на практике могут и не выполняться или выполняться приблизительно: например, среднее арифметическое элементов выборки является «эффективной» оценкой параметра 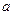 для выборки из нормального распределения N(
для выборки из нормального распределения N( 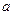 ,
, 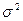 ): эта оценка несмещенная и обладает минимальной дисперсией. Но при отклонении распределения от нормального (например, при наличии «выбросов», т.е. резко выделяющихся значений), свойства этой оценки становятся неудовлетворительными, т.к. её значение очень сильно зависит от «выбросов».
): эта оценка несмещенная и обладает минимальной дисперсией. Но при отклонении распределения от нормального (например, при наличии «выбросов», т.е. резко выделяющихся значений), свойства этой оценки становятся неудовлетворительными, т.к. её значение очень сильно зависит от «выбросов».
 2. Доверительное оценивание.
2. Доверительное оценивание.
 Во многих случаях представляет интерес не получение точечной оценки
Во многих случаях представляет интерес не получение точечной оценки 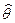 неизвестного параметра
неизвестного параметра  , а указание области (например, интервала на числовой прямой), в которой этот параметр находится с вероятностью, не меньшей заданной (скажем, 95 или 99%). Построить такую область можно следующим образом: выберем число
, а указание области (например, интервала на числовой прямой), в которой этот параметр находится с вероятностью, не меньшей заданной (скажем, 95 или 99%). Построить такую область можно следующим образом: выберем число 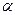 ,
, 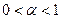 - вероятность, с которой параметр
- вероятность, с которой параметр  должен попасть в построенную нами область. Пусть мы имеем оценку
должен попасть в построенную нами область. Пусть мы имеем оценку 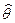 неизвестного параметра
неизвестного параметра  , и для каждого значения
, и для каждого значения  можем указать область
можем указать область 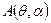 , в которой оценка
, в которой оценка 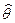 попадает с вероятностью не меньше
попадает с вероятностью не меньше 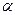 :
:

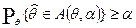
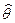
 Тогда, доверительной областью (в одномерном случае – доверительным интервалом) с уровнем доверия
Тогда, доверительной областью (в одномерном случае – доверительным интервалом) с уровнем доверия 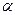 для неизвестного нам истинного значения
для неизвестного нам истинного значения  , построенной но наблюденному в опыте значению оценки
, построенной но наблюденному в опыте значению оценки 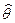 , является множество:
, является множество:

 .
.
 Можно сказать, что процесс доверительного оценивания является как бы обращением процесса проверки статистических гипотез: там мы по известному значению параметра
Можно сказать, что процесс доверительного оценивания является как бы обращением процесса проверки статистических гипотез: там мы по известному значению параметра  строили множество
строили множество 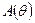 , в которое с заданной вероятностью попадает некоторая статистика, а здесь мы по таким множествам строим область, которая накрывает с заданной вероятностью само значение
, в которое с заданной вероятностью попадает некоторая статистика, а здесь мы по таким множествам строим область, которая накрывает с заданной вероятностью само значение  .
.
Лекция № 5
Доверительные пределы.
Если значение неизвестного параметра 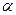 с вероятностью (1-p) заключено в интервале от
с вероятностью (1-p) заключено в интервале от 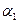
 до
до 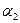 , то
, то 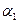 и
и 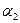 называются 100(1-p)% - ными доверительными пределами.
называются 100(1-p)% - ными доверительными пределами.
Выборки из нормального распределения.
Понятие доверительных пределов можно использовать для оценок параметров нормального распределения при наличии выборки любого объема.
1.Доверительные интервалы для среднего :

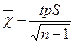 и
и 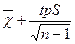 ,
,
где tp – абсолютное значение величины t (критерий Стьюдента) , для которого 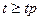 с вероятностью p при числе степеней свободы n-1.
с вероятностью p при числе степеней свободы n-1.
2.Доверительные пределы для среднего квадратичного отклонения:
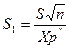 и
и 
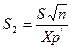 ,
,
где 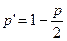 ,
, 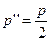 , а
, а  и
и 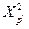 - значение
- значение 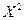 , для которых с вероятностью
, для которых с вероятностью 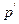 и
и  соответственно
соответственно 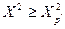 и
и 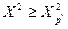 , при числе степеней свободы n-1.
, при числе степеней свободы n-1.
Следует отметить , что если n велико , то и распределение t , и распределение t , распределение 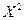 приближается к нормальному , в токах случаях применяется (2) более простые методы оценок : какое N можно считать «большим» - в некоторой степени зависит от уровня значимости , на котором проводится проверка – так при n = 10 и t = 3.29 вероятность t > 3.29 равна ~
приближается к нормальному , в токах случаях применяется (2) более простые методы оценок : какое N можно считать «большим» - в некоторой степени зависит от уровня значимости , на котором проводится проверка – так при n = 10 и t = 3.29 вероятность t > 3.29 равна ~  согласно нормальному распределению и ~
согласно нормальному распределению и ~ 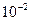 согласно распределению t – Стьюдента.
согласно распределению t – Стьюдента.
Большие выборки и приближенно нормальные оценки.
В случае выборок , не подчиняющихся нормальному распределению , не всегда удается найти доверительный интервал ; тем не менее этот метод применяют к выборкам большого объема , так как при этом считается , что распределение оценки обычно приближается к нормальному.
Таким образом , при большом N можно говорить о приближенных 100(1-p)% - ных доверительных пределах для параметра 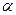 , которые даются в виде
, которые даются в виде
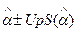 ,
,
где 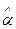 – оценка
– оценка 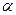 , S(
, S( 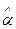 ) – её среднее квадратичное отклонение , Up – значение стандартизованной нормально распределенной величины , для которой U
) – её среднее квадратичное отклонение , Up – значение стандартизованной нормально распределенной величины , для которой U 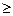 Up c вероятностью p. Такой метод дает надежные доверительные приделы для среднего значения , ели n
Up c вероятностью p. Такой метод дает надежные доверительные приделы для среднего значения , ели n 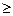 30 и распределение не сильно асимметрично; для оценок среднего квадратического отклонения , коэффициентов корреляции и т.п. объем выборки не должен превышать 100.
30 и распределение не сильно асимметрично; для оценок среднего квадратического отклонения , коэффициентов корреляции и т.п. объем выборки не должен превышать 100.
Метод максимального правдоподобия.
Оценка максимального правдоподобия.
Метод максимального правдоподобия ( наибольшего правдоподобия ) [ММП] представляет собой наиболее важный метод оценки параметров.
Пусть 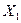 ,…,
,…, 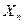 выборки из распределения , плотность которого в точке X зависит от неизвестного параметра
выборки из распределения , плотность которого в точке X зависит от неизвестного параметра  .Обозначим плотность отдельного наблюдения
.Обозначим плотность отдельного наблюдения 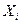 (i = 1, . . . ,n ) через p(X,
(i = 1, . . . ,n ) через p(X,  ) . Поскольку случайные величины
) . Поскольку случайные величины 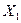 ,…,
,…, 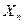 независимы , плотность вероятностей вектора (
независимы , плотность вероятностей вектора ( 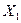 ,…,
,…, 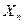 ) равна
) равна
p( 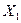 ,
,  )p(
)p( 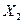 ,
,  ) ...p(
) ...p( 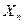 ,
,  ), где
), где  -неизвестное нам истинное значение параметра.
-неизвестное нам истинное значение параметра.
ММП состоит в следующем: подставим в это выражение вместо переменных ( 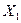 ,…,
,…, 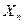 ) элементы выборки, т.е. реализация случайных величин
) элементы выборки, т.е. реализация случайных величин 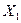 ,…,
,…, 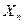 , а параметр
, а параметр  будем рассматривать как переменную величину ,изменяющуюся в заданной области значений. Получаем величину , которая называется функцией правдоподобия выборки :
будем рассматривать как переменную величину ,изменяющуюся в заданной области значений. Получаем величину , которая называется функцией правдоподобия выборки :
l ( 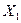 ,…,
,…, 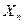 ;
;  ) = p(
) = p( 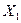 ,
,  )p(
)p( 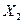 ,
,  ) ...p(
) ...p( 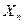 ,
,  ) =
) = 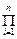 p(
p( 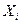 ,
,  )
)
ММП состоит в том ,что в качестве оценки неизвестного параметра  выбирается такое , что l (
выбирается такое , что l ( 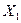 ,…,
,…, 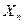 ;
;  ) → max, т.е. максимизирует функцию правдоподобия. В ряде случаев max удаётся найти аналитически, решая уравнение
) → max, т.е. максимизирует функцию правдоподобия. В ряде случаев max удаётся найти аналитически, решая уравнение
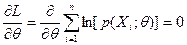 , где
, где
L=ln[l( 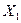 ,…,
,…, 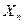 ;
;  )] – логарифмическая функция правдоподобия.
)] – логарифмическая функция правдоподобия.
Часто на практике не удаётся получить решение в аналитическом виде , и тогда для нахождения максимума прибегают к численным методам .
В подобных случаях , особенно когда выборка невелика и вид функции правдоподобия далек от нормального , целесообразно изображать функцию правдоподобия графически , откладывая по оси абсцисс значение оцениваемого параметра ( выбирая в качестве решения то значение ,где достигается max функции).
Ясно , что выбор  в качестве оценки
в качестве оценки  происходит в зависимости от значений
происходит в зависимости от значений 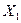 ,…,
,…, 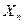 . Поэтому
. Поэтому  является случайной величиной.
является случайной величиной.
Пример : а) пусть случайная величина распределяется по нормальному закону с единичной дисперсией и неизвестным средним значением , т.е.

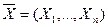
Тогда  ( множитель
( множитель 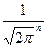 )
)
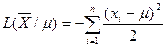
Функция 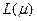 представляет собой квадратичную параболу ω переменной
представляет собой квадратичную параболу ω переменной 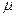 для любого n.
для любого n.
Эта функция достигает максимума при таком значении 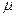 , для которого минимальна сумма
, для которого минимальна сумма
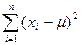
Поэтому, получаем результат, хорошо известный из МНК (метода наименьших квадратов):

Б) случай неизвестной дисперсии: если в рассмотренном примере дисперсия неизвестна, то возникает двухпараметрическая задача:
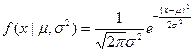
Следовательно:
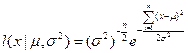
логарифмическая функция правдоподобия

Необходимо найти пару значений 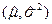 , которые с наибольшей вероятностью приводили бы к наблюдаемым значениям
, которые с наибольшей вероятностью приводили бы к наблюдаемым значениям  . Для этого нужно решить совместно два уравнения:
. Для этого нужно решить совместно два уравнения:
 и
и 
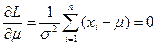 ,
,
откуда 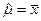
Далее 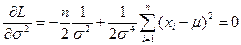 ,
,
Откуда 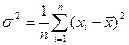
Видно, что оказывается смещенной оценкой дисперсии т.к.
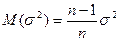
Дата добавления: 2018-06-28; просмотров: 1706;
