Оценка параметров экспоненциальных моделей
Оценка параметров экспоненциальных и S-образных кривых производится более сложными методами путём приведения их математических моделей к виду полинома первой степени:
Y = A + B · T (4.27)
с последующей дальнейшей оценкой коэффициентов A и B методом наименьших квадратов. Основной операцией при переходе от экспоненциальной модели к полиномиальной модели вида (4.27) является логарифмирование, а сам переход основан на использовании свойств логарифмов. После оценки параметров полинома (4.27) осуществляется обратный переход к исходной модели.
При определении параметров моделей, имеющих горизонтальные асимптоты, различают два случая. Если значение асимптоты h известно заранее, то путём модификации модели определение коэффициентов сводят к решению системы нормальных уравнений для полинома (4.27). Если значение асимптоты неизвестно, то для нахождения параметров кривых используются приближённые методы.
Таблица 4.1 – Оценка параметров экспоненциальных моделей (фрагмент).
| № п.п. | Функция | Преобразование | Прямой ход | Обратный ход |
| 1. | 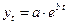
| 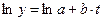
| 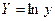 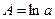
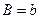 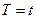
| 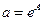
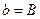
|
| 2. | 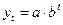
| 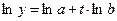
| 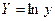 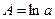
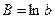 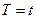
| 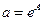
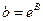
|
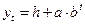
| 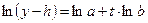 при
при 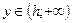
| 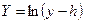 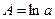
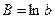 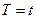
| 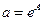
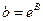
| |
| 3. | 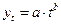
| 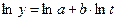
| 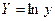 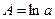
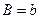 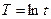
| 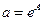
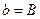
|
| 4. | 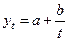
| 
| 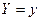 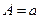
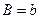 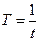
| 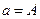
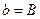
|
| 5. | 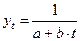
| 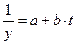
| 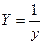 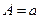 и т.д. и т.д.
| 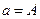
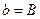
|
| … | … | … | … | … |
| 12. | 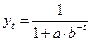
| 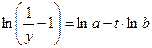 при
при 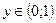
| 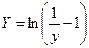 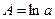
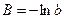 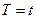
| 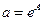
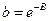
|
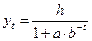
| 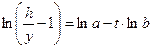 при
при 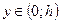
| 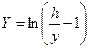 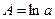
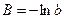 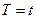
| 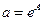
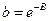
|
Такой подход привлекает своей универсальностью. Однако следует иметь ввиду, что полученные оценки являются смещёнными, т.к. в их вычислении участвуют не исходные значения, а их логарифмы. Смещение будет тем значительнее, чем больше разность между последовательными уровнями временного ряда. Не приводит к смещению в данном случае нелинейный метод наименьших квадратов.
Дата добавления: 2018-06-28; просмотров: 445;
