Энтропия системы. Принцип максимизации энтропии
В рассмотренном примере существовала возможность дать рекомендации для выбора решения, поскольку были известны вероятности случайных событий. Однако часто возникают ситуации, когда эти вероятности неизвестны.
Ранее в курсе рассматривались 3 вида неопределенностей в системах: а) из-за недостаточного знания; б) расплывчатость; в) случайная неопределенность.
Для неопределенности случайного объекта существует количественная мера (неопределенности), называется энтропией.
Рассмотрим простейший вариант – случайное событие. Пусть некоторое событие может произойти с вероятностью Р1 = 0,99 и не произойти с вероятностью Р2 = 0,01, а другое событие имеет вероятности Р1 = Р2 = 0,5. Очевидно, что в 1-м случае результатом опыта «почти наверняка» является наступление события, во втором случае неопределенность исхода так велика, что от прогноза лучше воздержаться.
Если мы имеем дело со случайной числовой величиной, то для характеристики различности распределений используется дисперсия или доверительный интервал.
Дх =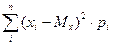 
для дискретной величины и
Дх =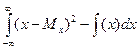 
Однако эти величины имеют смысл лишь для случайных числовых величин и не могут применяться к случайным объектам, состояния которых различаются качественно (например, выбор тех или иных команд или спортсменов при жеребьевке и т.п.).
Следовательно, мера неопределенности, связанной с распределением случайного события должна быть некоторой его числовой характеристикой, функционалом от распределения, но никак не связанным с тем, в какой шкале измеряются реализации случайного объекта.
Такой мерой неопределенности случайного объекта А с конечным множеством возможных состояний А1 …Аn с соответствующими вероятностями р1…рn величину,
Н = -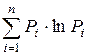 
которая называется энтропией случайного объекта А (или распределения {рi}).
Действительно, любая большая система может рассматриваться как система, которая принимает некоторое множество состояний S1, S2, …Sn с вероятностями Р1, Р2, ….Pn соответственно. Энтропия системы, будучи, как видно из формулы, математическим ожиданием логарифма вероятности пребывания системы в некотором состоянии S, рассматривается в качестве меры разнообразия для множества возможных состояний S.
Эта функция соответствует выделенной К.Шенноном в теории информации «мере неопределенности».
Если выбор любого состояния равновероятен, то неопределенность выбора максимальна и определяется общим числом возможных вариантов:
Н = -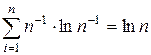 
.
Величина Н(n) эквивалентна понятию энтропии в статистической физике H = k×lnW, где W (Е) – статистический вес системы, или количество возможных квантовых состояний физической системы, внутренняя энергия которой не превосходит Е.ПОСТОЯННАЯБОЛЬЦМАНА (обозначение k), отношение универсальной ГАЗОВОЙ постоянной к ЧИСЛУАВОГАДРО, равное 1,381.10-23 джоулей на градус Кельвина. Оно указывает на взаимосвязь междукинетической энергией частицы газа (атома или молекулы) и ее абсолютной температурой. Названиепостоянной дано по имени ее открывателя Людвига БОЛЬЦМАНА.
В связи со всем сказанным выше можно записать и еще одно утверждение в отношении энтропии:
Дата добавления: 2018-03-01; просмотров: 381;