Режимы движения жидкости
Экспериментально установлено существование двух основных видов движения жидкости – ламинарного и турбулентного.
Ламинарным называют такой режим течения жидкости, когда все линии тока направлены параллельно оси канала, когда слои жидкости двигаются без перемешивания частиц и пульсаций скорости.
При турбулентном движении слои жидкости интенсивно перемешиваются, движение частиц не носит упорядоченного характера, траектории имеют вид замысловатых линий, наряду с основным перемещением в направлении оси канала малые объемы жидкости вращаются и перемещаются в направлении перпендикулярном оси канала.
Наглядно особенности течения при разных режимах можно наблюдать с помощью экспериментальной установки, в которой жидкость перемещается в стеклянной трубе, а для визуализации течения в основной поток жидкости вводят струйки подкрашенной жидкости с близким значением кинематического коэффициента вязкости. Схема установки и примерная картина изменения формы струйки подкрашенной жидкости показаны на рис. 7.4.
В расходном баке 1 с помощью внутренней перегородки 9 поддерживается постоянный уровень жидкости, что обеспечивает, при установленном с помощью крана 6 расходе жидкости, постоянную скорость ее движения в стеклянной трубке 2. К установившемуся потоку жидкости в трубке 2 подмешивается струйка подкрашенной жидкости из расходного бачка 3, которая подается через кран 4 по трубке 5.
До определенной скорости движения жидкости по трубке 2 заметного обмена частицами жидкости между окрашенной струйкой и окружающей ее жидкостью не происходит. Если в поток вводить несколько струек подкрашенной жидкости, то все они перемещаются не смешиваясь с остальной массой жидкости. Это позволяет утверждать, что при установленной скорости движения жидкость движется отдельными слоями не перемешивающимися между собой. Линии тока при этом прямолинейны и устойчивы. Средняя скорость движения жидкости, до которой наблюдается описанное явление, называют критической - 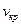 .
.
При увеличении скорости течения до значения больше критического, окрашенные струйки начинают искривляться; а при еще большем увеличении - струйки распадаются на отдельные хорошо различимые вихри, интенсивно перемешивающиеся с остальной массой жидкости.
При уменьшении скорости потока после достижения турбулентного режима течения явление повторяется в обратном порядке, но с одним отличием – скорость, на которой происходит переход от турбулентного режима течения к ламинарному оказывается меньше, чем при переходе от ламинарного к турбулентному. Ламинарный и турбулентный режимы отличаются величиной сопротивления движению потока. Потери напора при турбулентном движении больше. Качественно зависимость гидравлического уклона от скорости потока представлена на рис. 7.5.
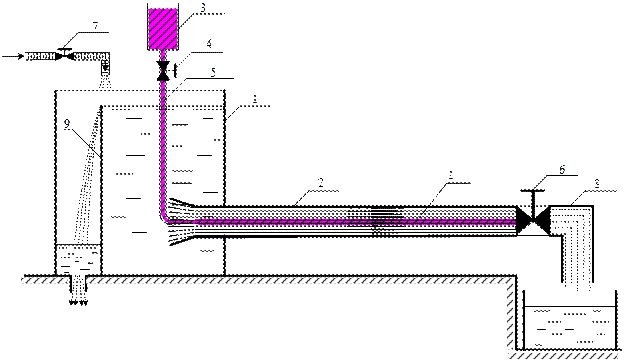
 Рис. 7.4.
Рис. 7.4.
|
В диапазоне скоростей 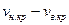 движение жидкости считают смешанным; при
движение жидкости считают смешанным; при 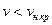 – ламинарным, а при
– ламинарным, а при 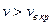 – турбулентным. Абсолютное значение критических скоростей зависит от кинематической вязкости жидкости и геометрических параметров живого сечения.
– турбулентным. Абсолютное значение критических скоростей зависит от кинематической вязкости жидкости и геометрических параметров живого сечения.
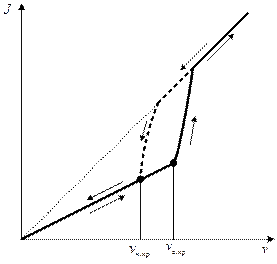 Рис. 7.5
Рис. 7.5
|
Для труб круглого сечения при напорном движении потока нижняя критическая скорость пропорциональна кинематической вязкости и обратно пропорциональна диаметру трубы
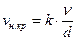 , ,
| (7.15) |
где коэффициент пропорциональности k остается неизменным при различных значениях 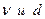 . Теория подобия гидравлических потоков позволила определить этот безразмерный коэффициент, как критическое значение числа подобия – числа Рейнольдса. Значение критического числа Рейнольдса установлено многочисленными экспериментами и равно 2300 для круглых труб.
. Теория подобия гидравлических потоков позволила определить этот безразмерный коэффициент, как критическое значение числа подобия – числа Рейнольдса. Значение критического числа Рейнольдса установлено многочисленными экспериментами и равно 2300 для круглых труб.
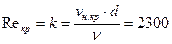 . .
| (7.16) |
Для каналов иной формы поперечного сечения и открытых русел характерный линейный размер необходимо заменить гидравлическим радиусом R, что изменит численное значение критического числа Рейнольдса. Так как для круглой трубы 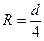 , формула (7.16) принимает вид (7.17) и может использоваться для вычисления нижней критической скорости
, формула (7.16) принимает вид (7.17) и может использоваться для вычисления нижней критической скорости
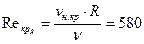 . .
| (7.17) |
Для открытого русла прямоугольного сечения в качестве характерного линейного размера часто выбирают глубину потока h. Если 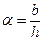 , где b – ширина русла, то легко получить формулу для расчета критического значения числа Рейнольдса
, где b – ширина русла, то легко получить формулу для расчета критического значения числа Рейнольдса 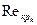 в зависимости от коэффициента
в зависимости от коэффициента 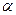
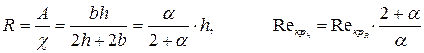 . .
| (7.18) |
При 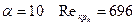 , а при
, а при 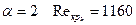 .
.
Дата добавления: 2017-12-07; просмотров: 656;
