Уравнение Бернулли для струйки реальной жидкости потока реальной жидкости. Режимы движения жидкости
Уравнение Бернулли для струйки вязкой жидкости
Течение реальной жидкости, в отличие от течения идеальной, характеризуется наличием потерь энергии на преодоление сил сопротивления движению – в первую очередь это потери на преодоление сил трения, обусловленных вязкостью жидкости и ее трением о стенки канала. Поэтому в правую часть формулы (6.35) необходимо добавить слагаемое, которое и будет учитывать потери энергии струйки
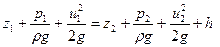 , ,
| (7.1) |
где 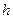 -- потери напора на участке между сечениями 1-1 и 2-2.
-- потери напора на участке между сечениями 1-1 и 2-2.
Энергия, затраченная на преодоление сил вязкого трения, превращается из механической энергии в энергию тепловую. Процесс носит необратимый характер.
Уравнение Бернулли для потока вязкой жидкости
при установившемся движении
Если движение жидкости установившееся и плавно изменяющееся происходит в направлении оси x, то
 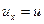 ; ; 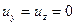 ; ; 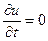 . .
| (7.2) |
В этом случае давление по живому сечению потока распределяется по гидростатическому закону, т.е.
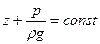 . .
| (7.3) |
Если поле скоростей имеет искривленные линии тока, гидростатический закон распределения давления в живом сечении нарушается, но при достаточной плавности потока этим фактом можно пренебречь (рис.7.1).
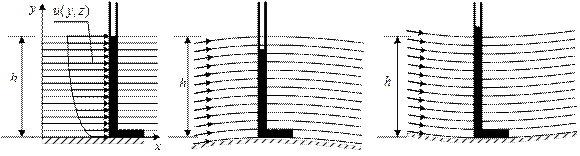 Рис. 7.1
Рис. 7.1
|
При переменной по сечению скорости частиц жидкости ( 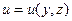 ), удельную кинетическую энергию массы жидкости, протекающей через живое сечение потока A можно рассчитать по формуле
), удельную кинетическую энергию массы жидкости, протекающей через живое сечение потока A можно рассчитать по формуле
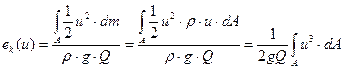 , ,
| (7.4) |
где 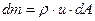 - масса жидкости, которая прошла через сечение за единицу времени.
- масса жидкости, которая прошла через сечение за единицу времени.
В общем случае вычисления по формуле (7.4) невозможны, т.к. функция  неизвестна. Целесообразно воспользоваться средней скоростью потока в сечении v
неизвестна. Целесообразно воспользоваться средней скоростью потока в сечении v
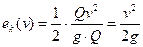 . .
| (7.5) |
Заменить в уравнении Бернулли для потока удельную кинетическую энергию 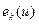 на
на 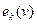 можно, если ввести коэффициент кинетической энергии (коэффициент Кориолиса)
можно, если ввести коэффициент кинетической энергии (коэффициент Кориолиса)
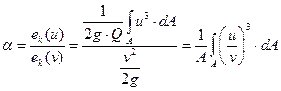 . .
| (7.6) |
В этом случае
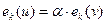 . .
| (7.7) |
Коэффициент 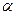 определяется для всех практически значимых случаев течения потока экспериментально и характеризует отношение действительной кинетической энергии массы жидкости, протекающей через живое сечение потока, к кинетической энергии той же массы жидкости, вычисленной по средней скорости потока в сечении.
определяется для всех практически значимых случаев течения потока экспериментально и характеризует отношение действительной кинетической энергии массы жидкости, протекающей через живое сечение потока, к кинетической энергии той же массы жидкости, вычисленной по средней скорости потока в сечении.
| Условия движения жидкости | ||
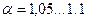
| - при прямолинейном турбулентном течении в трубах; | ||
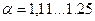
| - при прямолинейном турбулентном течении в открытых каналах; | ||
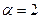
| - при прямолинейном ламинарном течении в трубах (теоретическое решение). |
Вводя в рассмотрение средние значения геометрического напора z и пьезометрического напора 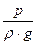 , запишем для плавно изменяющегося потока, ограниченного жесткими стенками (канал, русло, трубопровод) уравнение Бернулли
, запишем для плавно изменяющегося потока, ограниченного жесткими стенками (канал, русло, трубопровод) уравнение Бернулли
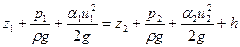 . .
| (7.8) |
Графическое толкование уравнения Бернулли для потока вязкой жидкости в предположении, что потери напора h линейно зависят от длины канала, приведено на рис. 7.2, где 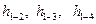 - потери напора на участке между сечениями 1-2, 1-3, 1-4 соответственно. Линия полного напора в этом случае не остается горизонтальной, как при движении идеальной жидкости, а представляет линию нисходящую по направлению движения потока.
- потери напора на участке между сечениями 1-2, 1-3, 1-4 соответственно. Линия полного напора в этом случае не остается горизонтальной, как при движении идеальной жидкости, а представляет линию нисходящую по направлению движения потока.
Для характеристики потерь напора на регулярном участке потока используют понятие гидравлического уклона. Гидравлический уклон – это величина средних потерь напора на единицу длины канала
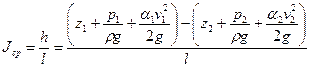 . .
| (7.9) |
Локальное гидравлического уклона характеризует скорость уменьшения полного напора потока по направлению его движения
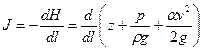 . .
| (7.10) |
 Рис.7.2.
Рис.7.2.
|
Классификация потерь напора
Потери напора при движении вязкой жидкости подразделяют на:
· потери напора на преодоление гидравлического сопротивления по длине, которые пропорциональны длине участков русла или трубы, направляющей движение потока;
· потери на преодоление гидравлических сопротивлений в пределах коротких участков, на которых имеются различные конструктивные нерегулярности – резкое сужение или расширение русла, внезапное увеличение или уменьшение диаметра трубы, поворот трубы или русла, устройства входа или выхода, трубопроводная арматура ( краны, задвижки, разветвления и т.д.).
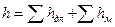
| (7.11) |
Обычно потери напора определяют через скоростной напор и соответствующий коэффициент сопротивления 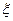
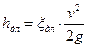 , ,
| (7.12) |
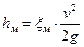 . .
| (7.13) |
Большинство зависимостей для определения коэффициентов сопротивления 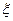 или их конкретные значения установлены экспериментальным путем. На значения коэффициентов сопротивления влияет множество факторов:
или их конкретные значения установлены экспериментальным путем. На значения коэффициентов сопротивления влияет множество факторов:
· конструктивные формы и размеры;
· шероховатость стенок канала или трубы;
· скоростной режим течения жидкости;
· положение управляющих элементов запорной арматуры.
Одна из общих формул для определения потерь по длине – формула Дарси-Вейсбаха, для круглых труб имеет вид
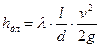 , ,
| (7.14) |
где 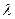 - коэффициент гидравлического трения;
- коэффициент гидравлического трения;
l - длина трубопровода;
d – диаметр трубы.
Очевидно, что в этом случае 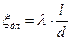 .
.
Коэффициенты местного сопротивления определяются исключительно экспериментальным путем и их значения можно найти в справочниках и учебниках. Обычно в формуле (7.12) коэффициент 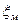 определяется применительно к скоростному напору за местным сопротивлением (рис.7.3)
определяется применительно к скоростному напору за местным сопротивлением (рис.7.3)
 Рис. 7.3
Рис. 7.3
| 
|
Дата добавления: 2017-12-07; просмотров: 733;
