Регрессионный анализ. 4 страница

12. –x₄= x₂x₃ x₅= –x₁x₂x₃

Допустим, выбран пятый вариант: x₄= x₁x₃ и x₅= x₁x₂x₃. Тогда определяющими контрастами являются: l=x₁x₃x₄ и 1=x₁x₂x₃x₅.

Если перемножить эти определяющие контрасты, то получится третье соотношение, задающее элементы столбца 1=x₂x₄x₅. Чтобы полностью охарактеризовать разрешающую способность реплики, необходимо записать обобщающий определяющий контраст 1 = x₁x₃x₄=x₂x₄x₅=x₁x₂x₃x₅

Система смешивания определяется умножением обобщающего определяющего контраста последовательно на х₁, х₂, х₃ и т. д.

x₁= x₃x₄= x₁x₂x₄x₅= x₂x₃x₅

x₂ = x₁x₂x₃x₄= x₄x₅= x₁x₃x₅

x₃= x₁x₄= x₂x₃x₄x₅= x₁x₂x₅

x₄= x₁x₃= x₂x₅= x₁x₂x₃x₄x₅

x₅= x₁x₃x₄x₅= x₂x₄= x₁x₂x₃

x₁x₂= x₂x₃x₄= x₁x₄x₅= x₃x₅

x₁x₅= x₃x₄x₅= x₁x₂x₄= x₂x₃

Получается довольно сложная система смешивания линейных эффектов с эффектами взаимодействия первого, второго, третьего и четвертого порядков. Если, например, коэффициенты b₁₂ и b₁₅ отличны от нуля, то возникают сомнения, можно ли пренебрегать другими парными взаимодействиями, с которыми смешаны линейные эффекты. Тогда следует поставить вторую серию опытов, выбрав нужным образом другую 1/4-реплику.

При этом можно воспользоваться методом «перевала». Смысл этого метода заключается в том, что вторая четверть-реплика получается из первой путем изменения всех знаков матрицы на обратные. Тогда в обобщающем определяющем контрасте тройные произведения имеют знак, противоположный их знаку в первой четверть-реплике. Тройные произведения определяют парные взаимодействия в совместных оценках для линейных эффектов. Усредняя результаты обеих четверть-реплик, можно получить линейные эффекты, не смешанные с парными взаимодействиями.

Для дополнения 1/4-реплики до 1/2-реплики, если есть подозрения, что эффекты взаимодействия первого порядка отличаются от нуля, нужно взять вторую четверть-реплику с обобщающим контрастом, в котором два тройных произведения имеют отрицательный знак, так как тройные произведения определяют парные взаимодействия в совместных оценках для линейных эффектов.

Однако можно представить себе и такой случай, когда целесообразно освободить линейные эффекты от эффектов взаимодействия второго порядка и только часть из линейных эффектов от парных взаимодействий. Тогда нужно выбрать 1/4-реплику таким образом, чтобы в обобщающем определяющем контрасте произведение четырех членов имело отрицательный знак, так как это произведение определяет тройные взаимодействия в совместных оценках для линейных эффектов.

4.8 Воспроизводимость эксперимента

Структура экспериментального исследования:

1. Принятие решений перед планированием эксперимента (анкета для сбора априорной информации)

2. Планирование эксперимента

3. Подготовка и проведение эксперимента

4. Предварительная обработка результатов

5. Обработка результатов эксперимента

1. Принятие решений перед планированием эксперимента (анкета для сбора априорной информации):

- постановка задачи, выбор откликов (параметров оптимизации):

а) краткое описание процесса, объекта исследования;

б) формулировка цели исследования и задач (если необходимо проранжировать по степени важности);

в) выбор откликов (составление таблицы откликов);

г) желаемый результат. Число и точность

д) какой результат будет считаться отличным, хорошим и т.д.;

- выбор факторов:

а) список всех подозреваемых факторов, которые могут влиять на процесс;

б) список факторов включаемых в эксперимент;

в) существуют ли возможности установления значения фактора на любом заданном уровне?

г) сохраняются ли заданные значения уровней в течении опыта?

д) могут ли комбинации факторов привести к остановке процесса?

- число опытов:

а) желаемое число опытов, ограничения на число опытов;

б) желаемый срок проведения исследования;

в) примерная длительность одного опыта;

г) стоимость и затраты труда при проведении одного опыта;

д) возможность проведения параллельных опытов и их желаемое число;

е) желаемая стратегия проведения опытов (по одному в день и тп.)

- учет априорной информации:

а) условия и результаты достигнутые при изучении аналогичных процессов;

б) результаты предварительного эксперимента и данные (литературные и собственные) о величине ошибки эксперимента;

в) взаимодействия факторов.

2. Планирование эксперимента:

- определение интервалов варьирования факторов;

- выбор математической модели процесса;

- составление матрицы планирования (ПФЭ или ДФЭ);

3. Подготовка и проведение эксперимента:

- разработка методики программы исследований (выбор технологии);

- выбор и обоснование средств измерений;

- конструирование приборов, макетов, аппаратов, моделей, стендов, установок и других средств эксперимента;

- проведение эксперимента в лаборатории, на опытных участках, на заводах, в фирмах;

Предварительная обработка результатов измерений и наблюдений необходима для того, чтобы в дальнейшем, при построении эмпирических зависимостей (функций отклика), с наибольшей эффективностью использовать статистические методы и корректно анализировать полученные результаты.

4. Предварительная обработка результатов состоит в:

- проверке однородности рядов наблюдений:

а) отсеивании грубых погрешностей;

б) проверке однородности нескольких дисперсий;

в) проверке воспроизводимости эксперимента;

- оценке достоверности результатов измерений - вычисление параметров эмпирических наблюдений:

а) точечное оценивание;

б) построение доверительного интервала для истинного значения;

в) построение доверительного интервала для дисперсии;

- проверке гипотез о виде распределения:

а) проверке соответствия результатов измерения нормальному закону;

б) определение параметра этого распределения.

5. Обработка результатов эксперимента:

- определение коэффициентов уравнения регрессии;

- проверка значимости коэффициентов;

- проверка адекватности модели;

- интерпретация результатов.

4.8.1 Требования к эксперименту по оценке прецизионности.

Программа исследований по ГОСТ Р ИСО 5725-2-2002 Точность (правильность и Прецизионность) методов и результатов измерений. Часть 2 Основной метод определения повторяемости и воспроизводимости стандартного метода измерений

1. Выполнение измерений должно быть организовано с соблюдением следующих требований.

a) Любая предварительная проверка оборудования должна соответствовать требованиям стандарта на метод измерений.

b) Каждая группа из n измерений, относящихся к одному уровню, должна осуществляться при соблюдении условий повторяемости, т.е. в пределах короткого интервала времени и одним и тем же оператором, а также без какой бы то ни было промежуточной перекалибровки аппаратуры, если только это не является неотъемлемой частью выполнения измерений.

c) Необходимо, чтобы группа из n измерений в условиях повторяемости выполнялась независимым образом так, как если бы это были n измерений на различных материалах. Тем не менее, как правило, оператор знает, что он исследует идентичный материал, и поэтому в инструкциях необходимо подчеркнуть, что главной целью эксперимента является определение именно различий (расхождений) в результатах, которые могут появиться при реальных испытаниях. Если же есть основания опасаться, что, несмотря на данное предостережение, предварительные результаты могут повлиять на последующие результаты измерений и, следовательно, на дисперсию повторяемости, то следует принять решение, включать ли в число п на каждом из q уровней некоторое количество проб (образцов) из других уровней, так чтобы оператор не знал, какие из них являются повторами для данного уровня (модифицировав таким перемешиванием основной метод). Такая методика, однако, могла бы создать трудности в обеспечении условий повторяемости в период между измерениями, т.к. в этом случае необходимо, чтобы все q групп из п измерений были осуществлены в пределах короткого интервала времени.

d) Однако при использовании основного метода «в чистом виде» не обязательно стремиться к тому, чтобы все q групп из п измерений были проведены в пределах короткого интервала времени; различные группы измерений могут проводиться в разные дни.

e) Измерения для всех q уровней должны выполняться одним и тем же оператором, и, кроме того, п измерений на данном уровне должны выполняться с использованием одного и того же оборудования.

f) Если в процессе измерений оператор не сможет их выполнить полностью, измерения может завершить другой оператор при условии, что замена оператора не произойдет в пределах группы из п измерении на одном уровне, т.е. замены операторов могут происходить лишь при переходе от одного уровня к другому. Любое такого рода изменение должно регистрироваться вместе с результатами.

g) Должен быть задан временной интервал проведения измерений, т.е. время между датой получения проб и датой завершения всех измерений.

h) Все пробы должны быть отчетливо промаркированы с указанием названия эксперимента и шифра пробы.

2. В 1 и других пунктах настоящего стандарта упоминается оператор. В действительности некоторые измерения может проводить группа операторов, каждый из которых выполняет какую-то специфическую часть процедуры. В этом случае группа должна рассматриваться как «оператор», и любое изменение в группе должно восприниматься как смена «оператора».

3. В коммерческой практике (торговле) результаты измерений (испытаний) могут округляться довольно грубо, однако в эксперименте по оценке прецизионности результаты должны регистрироваться (вычисляться) с точностью, по меньшей мере на один знак большей, чем количество значащих цифр, установленное для регистрации результатов измерений (испытаний) стандартным методом. Если метод не устанавливает количество значащих цифр, округление не должно быть грубее половины оценки стандартного отклонения повторяемости. Когда прецизионность зависит от уровня т, для различных уровней могут потребоваться различные степени округления.

4.8.2 Проверка воспроизводимости эксперимента.

Основная цель ТПЭ — построение математической модели исследуемого в экс­перименте процесса. Чтобы воспользоваться методами ТПЭ, нужно сначала убе­диться, что эксперимент воспроизводим.

Прецизионность (воспроизводимость) – степень близости друг к другу независимых результатов измерений, полученных в конкретных условия.

Под воспроизводимыми экспериментами понимаются такие, в процессе кото­рых в любой момент времени объект исследования и измерительное оборудова­ние можно вернуть в исходное состояние и эксперимент повторить. Например, испытывая двигатель и снимая его характеристики, можно предположить, что в любой момент или за относительно короткий отрезок времени можно вернуться к исходному режиму и воспроизвести его практически без каких-либо изменений.

Большинство экспериментов в науке и технике относится к невоспроизводи­мым. Наиболее яркий пример - исследование изнашивания детали какого-либо узла машины при испытаниях ее на надежность.

В процессе лабораторного или эксплуатационного эксперимента объект иссле­дования деформируется, меняя форму, или уменьшается в размерах. Такое про­грессирующее ухудшение технического состояния объекта исследований не по­зволит исследователю воспроизвести состояние, в котором объект был в начале исследования.

Для проверки воспроизводимости эксперимента проводят несколько серий па­раллельных опытов.

Параллельные опыты - опыты, проведенные несколько раз при одних и тех же значениях факторов. Результаты опытов заносятся в таблицу 2.1, где к - число параллельных опытов (обычно к = 2...4); N -число серий параллельных опытов.

Для каждой серии параллельных опытов вычисляют среднее арифметическое значение функции отклика по формуле (4.29)

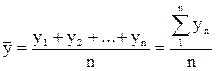, (4.29)

где n – количество параллельных опытов.

Отклонение результата любого опыта от среднего арифметического можно представить как разность (4.30).

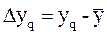, (4.30)

где y_q – результат отдельного опыта.

Наличие отклонения свидетельствует об изменчивости, вариации значений повторных опытов. Для измерения этой изменчивости чаще всего используют дисперсию. Дисперсией называется среднее значение квадрата отклонений величины от ее среднего значения. Дисперсия обозначается s² и выражается формулой (4.31).

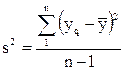, (4.31)

где n – 1 - число степеней свободы, равное количеству опытов минус единица. Одна степень свободы использована для вычисления среднего.

Корень квадратный из дисперсии, взятый с положительным знаком, называется средним квадратическим отклонением, стандартом или квадратичной ошибкой

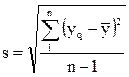. (4.32)

Стандарт имеет размерность той величины, для которой он вычислен. Дисперсия и стандарт – это меры рассеяния, изменчивости. Чем больше дисперсия и стандарт, тем больше рассеяны значения параллельных опытов около среднего значения.

Среднее арифметическое равно сумме всех n отдельных результатов, деленной на n, если они имеют нормальное распределение.

Наличие резко отклоняющихся результатов (грубых наблюдений) свидетельствует о нарушении закона нормального распределения.

При наличии грубых наблюдений их необходимо сначала исключить, а затем подсчитывать среднее арифметическое и дисперсию.

Ошибка опыта являемся суммарной величиной, результатом многих ошибок: ошибок измерений факторов, ошибок измерений параметра оптимизации и др. Каждую из этих ошибок можно, в свою очередь, разделить на составляющие.

Вопрос о классификации ошибок довольно сложный и вызывает много дискуссий. В качестве примера одной из возможных схем рассмотрим схему из книги Ю. В. Кельница «Теория ошибок измерений» (М., изд-во «Недра», 1967) изображенную на рисунке 4.13.

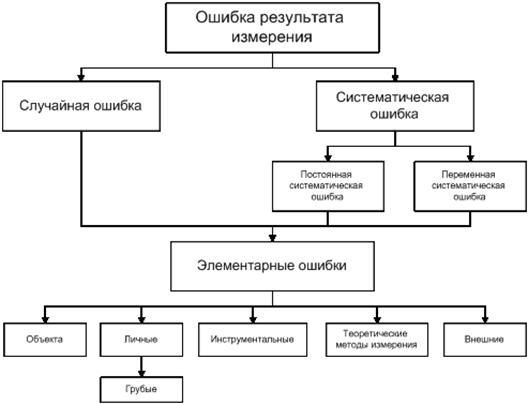
Рисунок 4.13 – Классификация ошибок измерения

Все ошибки принято разделять на два класса: систематические и случайные.

Систематические ошибки порождаются причинами, действующими регулярно, в определенном направлении. Чаще всего эти ошибки можно изучить и определить количественно.

Систематические ошибки находят, калибруя измерительные приборы и сопоставляя опытные данные с изменяющимися внешними условиями (например, при градуировке термопары по реперным точкам, при сравнении с эталонным прибором).

Если систематические ошибки вызываются внешними условиями (переменной температуры, сырья и т. д.), следует компенсировать их влияние. Как это делать, будет показано ниже.

Случайными ошибками называются те, которые появляются нерегулярно, причины возникновения которых неизвестны и которые невозможно учесть заранее.

Систематические и случайные ошибки состоят из множества элементарных ошибок. Для того, чтобы исключать инструментальные ошибки, следует проверять приборы перед опытом, иногда в течение опыта и обязательно после опыта. Ошибки при проведении самого опыта возникают вследствие неравномерного нагрева реакционной среды, разного способа перемешивания и т.п. При повторении опытов такие ошибки могут вызвать большой разброс экспериментальных результатов.

Очень важно исключить из экспериментальных данных грубые ошибки, так называемый брак при повторных опытах. Для отброса ошибочных опытов существуют правила. Для определения брака используют, например, критерий Стьюдента

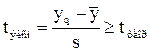, (4.33)

где y_q – предположительный брак выборки;

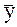- среднее арифметическое выборки без бракованного значения;

s – стандарт (квадратичная ошибка) выборки без брака.

Значение t берут из таблицы t-распределения Стьюдента (Приложения В). Опыт считается бракованным, если экспериментальное значение критерия t_эксп по модулю больше табличного значения.

Пример. При исследовании процесса коррозии четыре повторных опыта показали следующие значения скорости коррозии:

3,580, 2,370, 2,710 и 2,761 мг/см²·час.

Результат первого опыта поставлен под сомнение, так как он выделяется на фоне остальных трех опытов.

Исключим первый опыт из расчета и по остальным произведем вычисление среднего арифметического и стандарта:

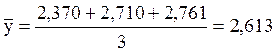
Δy_I = 2,370 – 2,613 = -0,243

Δy_II = 2,710 - 2,613 = 0,097

Δy_III = 2,761 - 2,613 = 0,148

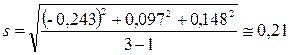
Если произведем проверку по критерию Стьюдента, то получим:

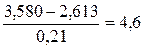
При числе степеней свободы f=2 и уровне значимости 0,05 (95%) t=4,303. экспериментальное значение больше табличного, поэтому сомнительный результат можно считать браком.

4.8.3 Дисперсия параметра оптимизации.

Дисперсия всего эксперимента получается в результате усреднения дисперсий всех опытов. По терминологии, принятой в планировании эксперимента, речь идет о подсчете дисперсии параметра оптимизации s²_{y} или, что то же самое, дисперсии воспроизводимости эксперимента s²_воспр.

При подсчете дисперсии параметра оптимизации по формуле (4.34), квадрат разности между значением y_q в каждом опыте и средним значением из n повторных наблюдений y нужно просуммировать по числу опытов в матрице N, а затем разделить на N(n - 1):

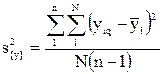, (4.34)

где i = 1, 2, …, N;

q = 1, 2, …, n.

Такой формулой можно пользоваться в случаях, когда число повторных опытов одинаково во всей матрице.

Дисперсию воспроизводимости проще всего рассчитывать, когда соблюдается равенство числа повторных опытов во всех экспериментальных точках. На практике весьма часто приходится сталкиваться со случаями, когда число повторных опытов различно. Это происходит вследствие отброса грубых наблюдений, неуверенности экспериментатора в правильности некоторых результатов (в таких случаях возникает желание еще и еще раз повторить опыт) и т.п.

Тогда при усреднении дисперсий приходится пользоваться средним взвешенным значением дисперсий, взятым с учетом числа степеней свободы

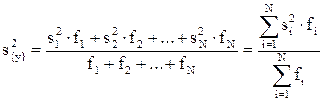, (4.35)

где 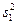- дисперсия первого опыта;

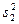- - дисперсия второго опыта и т.д.;

f₁ – число степеней свободы в первом опыте, равное числу параллельных опытов n₁ минус 1, т.е.

f₁ = n₁ – 2, (4.36)

f₂ – число степеней свободы во втором опыте и т.д.

Число степеней свободы средней дисперсии принимается равным сумме чисел степеней свободы дисперсий, из которых она вычислена.

Случай с неравным числом наблюдений, который мы рассмотрели выше, связан с нарушением ортогональности матрицы. Поэтому здесь нельзя использовать расчетные формулы для коэффициентов, приведенные ранее. Этот вопрос будет рассмотрен ниже.

Экспериментатору не следует забывать о проверке однородности дисперсий, неоднородные дисперсии усреднять нельзя. Прежде чем пользоваться приведёнными выше формулами, нужно убедиться в однородности суммируемых дисперсий.

4.8.4 Проверка однородности дисперсий.

Проверка однородности дисперсий производится с помощью различных статистических критериев.

- критерий Фишера, предназначенный для сравнения двух дисперсий (s=2, );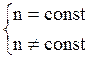

- критерий Кохрана, если сравниваемое количество дисперсий больше двух, но при одинаковом числе повторных опытов (s > 2, n = const);

- критерий Бартлера, если сравниваемое количество дисперсий больше двух, при разном числе повторных опытов (s > 2, n ≠ const).

Простейшим из них является критерий Фишера, предназначенный для сравнения двух дисперсий. Критерий Фишера (F-критерий) представляет собою отношение большей дисперсии к меньшей (формула 4.37). Полученная величина сравнивается с табличной величиной F-критерия.

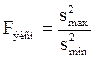. (4.37)

Если полученное значение дисперсионного отношения больше приведенного в таблице (приложения Г) для соответствующих степеней свободы и выбранного уровня значимости, это означает, что дисперсии значимо отличаются друг от друга, т. е. что они неоднородны.

Пример. Пусть s₁²=5,14, n₁=7 и f₁=6; s₂²=0,324, n₂=6 и f₂=5. в данном примере отношение дисперсий равно

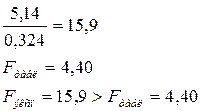
Если сравниваемое количество дисперсий больше двух и одна дисперсия значительно превышает остальные, можно воспользоваться критерием Кохрена. Этот критерий пригоден для случаев, когда во всех точках имеется одинаковое число повторных опытов. При этом подсчитывается дисперсия в каждой горизонтальной строке матрицы по формуле (4.31):

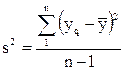
а затем из всех дисперсий находится наибольшая s²_max которая делится на сумму всех дисперсий. Критерий Кохрена– это отношение максимальной дисперсии к сумме всех дисперсий, формула (4.38).

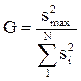. (4.38)

С этим критерием связаны числа свободы:

- f₁ = n – 1,

- F₂ = N.

Гипотеза об однородности дисперсий подтверждается, если экспериментальное значение критерия Кохрена не превышает табличного значения (Приложение Д). Тогда можно усреднять дисперсии и пользоваться формулой (4.34) воспроизводимости дисперсий:

.

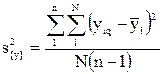Пример. Результаты эксперимента с 2я повторными опытами

№	y'	y''		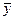Δy	(Δy)2	s2i
	80,23	81,93	81,08	-0,85	0,722	1,44
	86,50	84,80	85,65	0,85	0,722	1,44
	82,45	82,10	82,27	0,18	0,031	0,062
	89,50	91,30	90,40	-0,90	0,810	1,620
	85,10	84,80	84,95	0,15	0,023	0,046
	90,30	89,60	89,95	0,35	0,123	0,246
	85,60	84,90	85,25	0,35	0,123	0,246
	88,02	88,48	88,25	-0,23	0,053	0,106
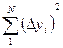
					2,607

Дисперсия в каждом опыте равна

.

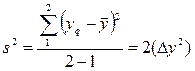Максимальная дисперсия оказалась в опыте №4.

Экспериментальный критерий Кохрена равен

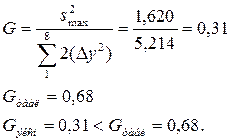
Экспериментальный критерий Кохрена не превышает значения табличного. Гипотеза об однородности дисперсий подтверждается.

Дисперсия воспроизводимости равна

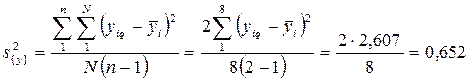
Если возникает предположение о наличии неоднородности дисперсий для случая, когда число повторных опытов неодинаково во всех точках, можно воспользоваться критерием Бартлета. По уже знакомой формуле (4.35) подсчитывается дисперсия воспроизводимости:

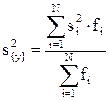
Далее находится величина по формуле (4.39).

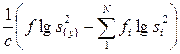, (4.39)

где c определяется по формуле (4.30)

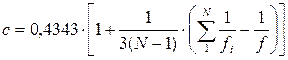. (4.40)

Здесь число степеней свободы равно N-1, где N – число сравниваемых дисперсий. При планировании эксперимента типа 2^k это число равно числу опытов в матрице.

Бартлет показал, что величина 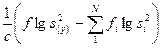приближенно подчиняется χ² – распределению с (N–1) степенями свободы. Значимость критерия Бартлета проверяется обычным способом.

Критерий Бартлета базируется на нормальном распределении. Если имеются отклонения от нормального распределения, то проверка неоднородности дисперсий может привести к ошибочным результатам.

Можно предложить использование F-критерия даже в тех случаях, когда число дисперсий больше двух. Делается это следующим образом. Из всех дисперсий выделяются наибольшая и наименьшая. По F-критерию производится проверка, значимо ли они различаются между собой. Ясно, что если наибольшая и наименьшая дисперсии не отличаются значимо, то дисперсии, имеющие промежуточные значения, также не могут значимо отличаться друг от друга. Тогда всю группу дисперсий можно считать принадлежащей к единой совокупности. В таких случаях нет надобности применять критерий Бартлета.

4.8.5 Рандомизация.

Чтобы исключить влияние систематических ошибок, вызванных внешними условиями (переменой температуры, сырья, лаборанта и т. д.), рекомендуется случайная последовательность при постановке опытов, запланированных матрицей. Опыты необходимо рандомизировать во времени. Термин «рандомизация» происходит от английского слова random – случайный.

Почему рандомизация опытов важна, мы попытаемся показать на следующем примере.