Приложение 3. Значения F-критерия Фишера
при уровне значимости a = 0,05
| ν1 ν2 | 
| ||||||||||
| 161,5 | 215,7 | 224,6 | 230,2 | 238,9 | 243,9 | 254,3 | |||||
| 18,5 | 19,16 | 19,25 | 19,3 | 19,33 | 19,37 | 19,41 | 19,45 | 19,5 | |||
| 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,84 | 8,74 | 8,64 | 8,53 | ||
| 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,04 | 5,91 | 5,77 | 5,63 | ||
| 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,82 | 4,68 | 4,53 | 4,36 | ||
| 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,15 | 3,84 | 3,67 | |||
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,73 | 3,57 | 3,41 | 3,23 | ||
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,44 | 3,28 | 3,12 | 2,93 | ||
| 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,23 | 3,07 | 2,9 | 2,71 | ||
| 4,96 | 4,1 | 3,71 | 3,48 | 3,33 | 3,22 | 3,07 | 2,91 | 2,74 | 2,54 | ||
| 4,84 | 3,98 | 3,59 | 3,36 | 3,2 | 3,09 | 2,95 | 2,79 | 2,61 | 2,4 | ||
| 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 2,85 | 2,69 | 2,5 | 2,3 | |||
| 4,67 | 3,8 | 3,41 | 3,18 | 3,02 | 2,92 | 2,77 | 2,6 | 2,42 | 2,21 | ||
| 4,6 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,7 | 2,53 | 2,35 | 2,13 | ||
| 4,54 | 3,68 | 3,29 | 3,06 | 2,9 | 2,79 | 2,64 | 2,48 | 2,29 | 2,07 | ||
| 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,59 | 2,42 | 2,24 | 2,01 | ||
| 4,45 | 3,59 | 3,2 | 2,96 | 2,81 | 2,7 | 2,55 | 2,38 | 2,19 | 1,96 | ||
| 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,51 | 2,34 | 2,15 | 1,92 | ||
| 4,38 | 3,52 | 3,13 | 2,9 | 2,74 | 2,63 | 2,48 | 2,31 | 2,11 | 1,88 | ||
| 4,35 | 3,49 | 3,1 | 2,87 | 2,71 | 2,6 | 2,45 | 2,28 | 2,08 | 1,84 | ||
| 4,32 | 3,47 | 3,07 | 2,84 | 2,68 | 2,57 | 2,42 | 2,25 | 2,05 | 1,81 | ||
| 4,3 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,4 | 2,23 | 2,03 | 1,78 | ||
| 4,28 | 3,42 | 3,03 | 2,8 | 2,64 | 2,53 | 2,38 | 2,2 | 1,76 | |||
| 4,26 | 3,4 | 3,01 | 2,78 | 2,62 | 2,51 | 2,36 | 2,18 | 1,98 | 1,73 | ||
| 4,24 | 3,38 | 2,99 | 2,76 | 2,6 | 2,49 | 2,34 | 2,16 | 1,96 | 1,71 | ||
| 4,22 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,32 | 2,15 | 1,95 | 1,69 | ||
| 4,21 | 3,35 | 2,96 | 2,73 | 2,57 | 2,46 | 2,3 | 2,13 | 1,93 | 1,67 | ||
| 4,2 | 3,34 | 2,95 | 2,71 | 2,56 | 2,44 | 2,29 | 2,12 | 1,91 | 1,65 | ||
| 4,18 | 3,33 | 2,93 | 2,7 | 2,54 | 2,43 | 2,28 | 2,1 | 1,9 | 1,64 | ||
| 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,27 | 2,09 | 1,89 | 1,62 | ||
| 4,12 | 3,26 | 2,87 | 2,64 | 2,48 | 2,37 | 2,22 | 2,04 | 1,83 | 1,57 | ||
| 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,18 | 1,79 | 1,52 | |||
| 4,06 | 3,21 | 2,81 | 2,58 | 2,42 | 2,31 | 2,15 | 1,97 | 1,76 | 1,48 | ||
| 4,03 | 3,18 | 2,79 | 2,56 | 2,4 | 2,29 | 2,13 | 1,95 | 1,72 | 1,44 | ||
| 3,15 | 2,76 | 2,52 | 2,37 | 2,25 | 2,1 | 1,92 | 1,7 | 1,39 | |||
| 3,98 | 3,13 | 2,74 | 2,5 | 2,35 | 2,23 | 2,07 | 1,89 | 1,67 | 1,35 | ||
| 3,96 | 3,11 | 2,72 | 2,49 | 2,33 | 2,21 | 2,06 | 1,88 | 1,65 | 1,31 | ||
| 3,95 | 3,1 | 2,71 | 2,47 | 2,32 | 2,2 | 2,04 | 1,86 | 1,64 | 1,28 | ||
| 3,94 | 3,09 | 2,7 | 2,46 | 2,3 | 2,19 | 2,03 | 1,85 | 1,63 | 1,26 | ||
| 3,92 | 3,07 | 2,68 | 2,44 | 2,29 | 2,17 | 2,01 | 1,83 | 1,6 | 1,21 | ||
| 3,9 | 3,06 | 2,66 | 2,43 | 2,27 | 2,16 | 1,82 | 1,59 | 1,18 | |||
| 3,89 | 3,04 | 2,65 | 2,42 | 2,26 | 2,14 | 1,98 | 1,8 | 1,57 | 1,14 | ||
| 3,87 | 3,03 | 2,64 | 2,41 | 2,25 | 2,13 | 1,97 | 1,79. | 1,55 | 1,1 | ||
| 3,86 | 3,02 | 2,63 | 2,4 | 2,24 | 2,12 | 1,96 | 1,78 | 1,54 | 1,07 | ||
| 3,86 | 3,01 | 2,62 | 2,39 | 2,23 | 2,11 | 1,96 | 1,77 | 1,54 | 1,06 | ||
| 3,85 | 2,61 | 2,38 | 2,22 | 2,1 | 1,95 | 1,76 | 1,53 | 1,03 | |||
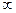
| 3,84 | 2,99 | 2,6 | 2,37 | 2,21 | 2,09 | 1,94 | 1,75 | 1,52 |
[1] f – это начальная буква англ. слова frequency – частота
[2] В статистике, в отличие от математики, пределы суммирования не ставятся, а подразумеваются, так как абсолютные величины здесь не абстрактные, а смысловые (суммируются все величины совокупности – с первой по последнюю)
[3] Во многих учебниках по статистике встречается другое название индекса динамики – темп роста. Использование такого названия не совсем логично, так динамика может быть различна (не только рост, но и спад, а также стабильность), поэтому наиболее правильным является использование названия «индекс динамики» или «индекс изменения»
[4] Часто встречается и другое название темпа изменения – темп прироста, что не совсем логично (см. предыдущую сноску)
[5] Обычно (в т.ч. и в дальнейшем в данном пособии) в статистических формулах пределы суммирования не ставятся, а подразумеваются, т.е. подразумеваются именно такие пределы как формуле (11) – с 1-ой группы по N-ю (последнюю)
[6] Если приходится иметь дело с интервальным рядом распределения с неравными интервалами, то для сопоставимости нужно частоты или частости привести к единице интервала, полученное значение называется плотностью ρ, то есть ρ = f/h
[7] Единицы совокупности, имеющие значение признака, равное границе интервала, включаются в тот интервал, где это точное значение впервые указывается
[8] От греч. «гистос» – ткань, строение
[9] От греч. слов «поли» и «гонос» – многоугольник
[10] При четном числе единиц совокупности за медиану принимают полусумму из двух центральных вариант
[11] Получите формулы и произведите их расчет (по аналогии с формулами для расчета квартилей) самостоятельно
[12] Максимально возможные значения показателей вариации: Лmax = 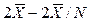 ;
; 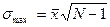 ;
; 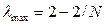 ;
; 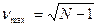
[13] При расчете параметров уравнения тренда на ЭВМ необходимость вести отсчет от середины ряда динамики отпадает. Например, для получения уравнения тренда в Microsoft Office Excel необходимо построить его график с помощью «Мастера диаграмм», после чего вызвать контекстное меню, нажав на правую кнопку мыши на построенном графике, и выбрать пункт «Добавить линию тренда», в появившемся окне выбрать подходящую математическую функцию и установить галочку «показывать уравнение на диаграмме»
[14] Используется при малом количестве уровней (n<30), в противном случае (n>30) вместо 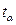 используют коэффициент доверия t нормального закона распределения (Приложение 1)
используют коэффициент доверия t нормального закона распределения (Приложение 1)
[15] Проявление стохастических связей подвержено действию закона больших чисел: лишь в достаточно большом числе единиц индивидуальные особенности сгладятся, случайности взаимопогасятся и зависимость, если она имеет существенную силу, проявится достаточно отчетливо
[16] Термин «стохастический» происходит от греч. «stochos» – мишень. Стреляя в мишень, даже хороший стрелок редко попадает в ее центр, выстрелы ложатся в некоторой близости от него. Другими словами стохастическая связь означает приблизительный характер значений признака
[17] Термин «корреляция» ввел в статистику английский биолог и статистик Ф. Гальтон в конце XIX в., под которым понималась «как бы связь», т.е. связь в форме, отличающейся от функциональной. Еще ранее этот термин применил француз Ж.Кювье в палеонтологии, где под законом корреляции частей животных он понимал возможность восстановить по найденным в раскопках частям облик всего животного
[18] Множественная корреляция изучается в курсе эконометрики на основе применения компьютерных программ (напр., специальная надстройка к Excel, SPSS и др.), в курсе статистики изучается только парная корреляция
[19] Данное условие означает отстутствие автокорреляции в коррелируемых рядах динамики, проверка на данное условие изучается на дневной форме обучения (при необходимости – см. конспект лекций для дневного отделения)
[20] Проделать это самостоятельно
[21] Термин «регрессия» ввел в статистику Ф. Гальтон, который изучив большое число семей, установил, что в группе семей высокорослыми отцами сыновья в среднем ниже ростом, чем их отцы, а в группе семей с низкорослыми отцами сыновья в среднем выше отцов, т.е. отклонение роста от среднего в следующем поколении уменьшается – регрессирует
[22] Параметры a0 и a1 можно получить не только методом подстановки как приводится далее, но и методом определителей 2-го порядка (проделать данное задание самостоятельно)
[23] Сумма эмпирических (2864,09) и выравненных по прямой линии (2864,115) значений должна совпадать, но в нашем случае этого не происходит из-за округлений расчетов до 3-х знаков после запятой
[24] В числителе – сумма последнего столбца, а в знаменателе – сумма предпоследнего столбца таблицы 22
| <== предыдущая лекция | | | следующая лекция ==> |
| | | ОСНОВНІ ЕТАПИ РОЗВИТКУ ДАВНЬОГРЕЦЬКОЇ АРХІТЕКТУРИ |
Дата добавления: 2017-12-05; просмотров: 308;
