Квадратурный делитель мощности (шлейфный мост)
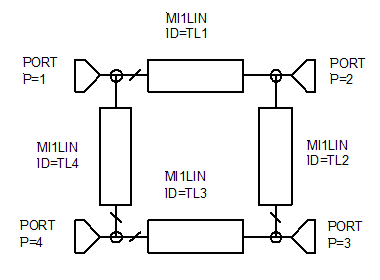


 Квадратурный делитель мощности ̶̶ это устройство с четырьмя портами (восьмиполюсник) предназначенное для получения двух сигналов половинной (по сравнению с входной) мощности, сдвинутых пофазе друг относительно друга на
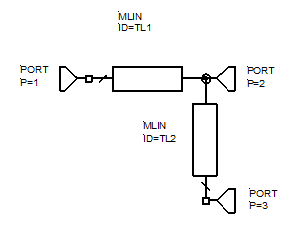
Квадратурный делитель мощности ̶̶ это устройство с четырьмя портами (восьмиполюсник) предназначенное для получения двух сигналов половинной (по сравнению с входной) мощности, сдвинутых пофазе друг относительно друга на 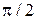 . Порты соединяются отрезками ЛП так, чтобы обеспечить заданный алгоритм функционирования устройства. Структура устройства изображена на рис. 2.2. Так как это МУ представляет собой восьмиполюсник, то матрица рассеяния его имеет следующий вид:
. Порты соединяются отрезками ЛП так, чтобы обеспечить заданный алгоритм функционирования устройства. Структура устройства изображена на рис. 2.2. Так как это МУ представляет собой восьмиполюсник, то матрица рассеяния его имеет следующий вид: 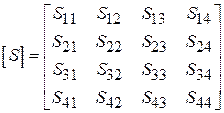 . Структура имеет две плоскости симметрии –
. Структура имеет две плоскости симметрии –
горизонтальную и вертикальную и поэтому должны выполняться условия:
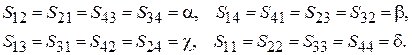 На основе свойства унитарности матрицы рассеяния структуры без потерь можно получить систему уравнений относительно коэффициентов
На основе свойства унитарности матрицы рассеяния структуры без потерь можно получить систему уравнений относительно коэффициентов 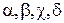 . Однако для упрощения сразу наложим условия на свойства МУ, потребовав, чтобы все порты были согласованы и волны выходили только из портов, лежащих на стороне, противоположной той, на которой находится возбуждающий порт. В этом случае коэффициенты
. Однако для упрощения сразу наложим условия на свойства МУ, потребовав, чтобы все порты были согласованы и волны выходили только из портов, лежащих на стороне, противоположной той, на которой находится возбуждающий порт. В этом случае коэффициенты 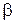 и
и 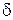 обращаются в ноль, и ранее упомянутые уравнения принимают вид:
обращаются в ноль, и ранее упомянутые уравнения принимают вид: 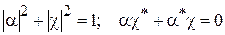 .
.

 Можно показать, что последнее уравнение сводится к уравнению
Можно показать, что последнее уравнение сводится к уравнению 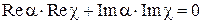 . Принимая во внимание, что мощности в выходных портах должны быть равны половине мощности возбуждения,
. Принимая во внимание, что мощности в выходных портах должны быть равны половине мощности возбуждения, 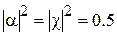 . Пусть сигнал на верхнем выходном порту равен
. Пусть сигнал на верхнем выходном порту равен 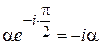 , а на нижнем выходном порту ‒
, а на нижнем выходном порту ‒ 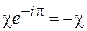 . Здесь
. Здесь 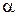 и
и 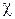 – вещественные числа. Очевидно, что вышеприведенное уравнение удовлетворяется, так как оба его слагаемых по отдельности равны нулю. Таким образом, матрица рассеяния шлейфного МУ имеет вид:
– вещественные числа. Очевидно, что вышеприведенное уравнение удовлетворяется, так как оба его слагаемых по отдельности равны нулю. Таким образом, матрица рассеяния шлейфного МУ имеет вид: 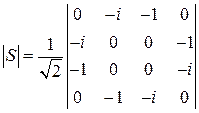 . Для определения волновых сопротивлений отрезков линий передачи закоротим порт 4, пользуясь тем, что сигнал на этом порту равен нулю. Так как условия, накладываемые на сигналы в выходных портах, требуют, чтобы все отрезки имели длину
. Для определения волновых сопротивлений отрезков линий передачи закоротим порт 4, пользуясь тем, что сигнал на этом порту равен нулю. Так как условия, накладываемые на сигналы в выходных портах, требуют, чтобы все отрезки имели длину 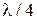 , то, принимая во внимание, что закороченная линия такой длины имеет бесконечно большое входное сопротивление, эквивалентная структура будет иметь вид, показанный на рис. 2.3. Предположим, что сопротивления нагрузок портов 2 и 3 равны
, то, принимая во внимание, что закороченная линия такой длины имеет бесконечно большое входное сопротивление, эквивалентная структура будет иметь вид, показанный на рис. 2.3. Предположим, что сопротивления нагрузок портов 2 и 3 равны 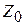 и волновое сопротивление линии TL2 также
и волновое сопротивление линии TL2 также 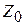 . Для того чтобы входной порт 1 был согласован с волновым сопротивлением питающей линии, равным
. Для того чтобы входной порт 1 был согласован с волновым сопротивлением питающей линии, равным 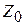 , необходимо, чтобы волновое сопротивление
, необходимо, чтобы волновое сопротивление 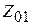 четвертьволнового отрезка TL1 было бы равно
четвертьволнового отрезка TL1 было бы равно 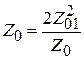 , так как сопротивление на его входе равно
, так как сопротивление на его входе равно 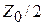 . Отсюда следует, что
. Отсюда следует, что 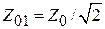 . Очевидно, что такое волновое сопротивление должно быть у верхнего и нижнего отрезков (TL1 и TL3), а у боковых отрезков (TL2 и TL4) волновое сопротивление должно быть равно
. Очевидно, что такое волновое сопротивление должно быть у верхнего и нижнего отрезков (TL1 и TL3), а у боковых отрезков (TL2 и TL4) волновое сопротивление должно быть равно  . В приложении приведена теория шлейфного моста с неравными значениями мощностей в плечах 2 и 3.
. В приложении приведена теория шлейфного моста с неравными значениями мощностей в плечах 2 и 3.
2.4. Синфазный-противофазный делитель мощности (гибридное кольцо)

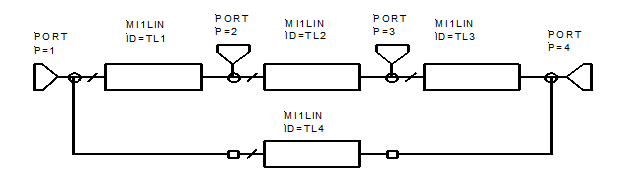 Гибридное кольцо ̶ это также восьмиполюсник или МУ с четырьмя портами. Структура его, показанная на рис. 2.4, такая же, как и у предыдущего МУ. Пусть левый есть порт 1, правый ─ порт 4, правее TL2 ─ порт 3, левее ─ порт 2. Структура имеет только одну плоскость симметрии ─ вертикальную, проходящую через отрезки TL2 и TL4, и поэтому должны выполняться равенства:
Гибридное кольцо ̶ это также восьмиполюсник или МУ с четырьмя портами. Структура его, показанная на рис. 2.4, такая же, как и у предыдущего МУ. Пусть левый есть порт 1, правый ─ порт 4, правее TL2 ─ порт 3, левее ─ порт 2. Структура имеет только одну плоскость симметрии ─ вертикальную, проходящую через отрезки TL2 и TL4, и поэтому должны выполняться равенства: 

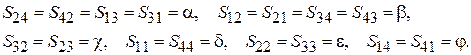
Для упрощения дальнейших выкладок потребуем, чтобы МУ было согласовано по всем четырем портам, откуда следует равенство 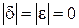 . Если возбуждать порт 2, то мощности синфазных сигналов в портах 1 и 3 должны быть равны половине мощности возбуждения; следовательно, модули
. Если возбуждать порт 2, то мощности синфазных сигналов в портах 1 и 3 должны быть равны половине мощности возбуждения; следовательно, модули 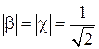 . Предположим также, что порты 1 и 3 развязаны и
. Предположим также, что порты 1 и 3 развязаны и 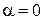 , что также обеспечивает развязку портов 2 и 4. Тогда, исходя из свойства унитарности матрицы рассеяния, остаются следующие уравнения:
, что также обеспечивает развязку портов 2 и 4. Тогда, исходя из свойства унитарности матрицы рассеяния, остаются следующие уравнения: 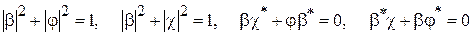 . Второе уравнение удовлетворяется автоматически, из первого и второго следует, что
. Второе уравнение удовлетворяется автоматически, из первого и второго следует, что 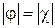 . Посмотрим теперь, каким образом могут быть удовлетворены 2 последних уравнения. Отрезки ЛП, которые связывают порты, должны иметь длины, равные нечетному числу четвертей длин волн. Это необходимо, чтобы сопротивления нагруженных портов трансформировались в возбуждающий порт для обеспечения согласования. Пусть возбуждающим является порт 2, а нагрузочными ─ порты 1 и 3. Тогда длины отрезков TL1 и TL2 равны
. Посмотрим теперь, каким образом могут быть удовлетворены 2 последних уравнения. Отрезки ЛП, которые связывают порты, должны иметь длины, равные нечетному числу четвертей длин волн. Это необходимо, чтобы сопротивления нагруженных портов трансформировались в возбуждающий порт для обеспечения согласования. Пусть возбуждающим является порт 2, а нагрузочными ─ порты 1 и 3. Тогда длины отрезков TL1 и TL2 равны 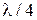 и, следовательно, выполняется равенство
и, следовательно, выполняется равенство 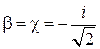 . При этом должно удовлетвориться уравнение
. При этом должно удовлетвориться уравнение 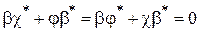 . Очевидно, что это возможно при
. Очевидно, что это возможно при 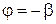 . Следовательно,
. Следовательно, 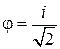 , а это означает, что длина отрезка TL4 равна
, а это означает, что длина отрезка TL4 равна 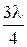 . Так как
. Так как 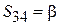 , то длина отрезка TL3 равна
, то длина отрезка TL3 равна 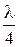 . Матрица рассеяния такого МУ:
. Матрица рассеяния такого МУ: 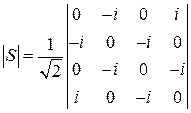 .
.
Найдем волновые сопротивления отрезков ЛП. Для определения волновых сопротивлений отрезков TL1 и TL2 поступим так же, как и в 2.3, замкнув накоротко порт 4. После этого получим структуру, полностью совпадающую со структурой мостового делителя мощности на 2 (см. 2.1). Очевидно, что волновые сопротивления должны удовлетворять соотношению 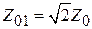 , где
, где 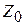 ─ волновое сопротивление линий, питающих порты. Для определения волновых сопротивлений отрезков TL3 и TL4 закоротим порт 1, питая МУ через порт 4. Полученная в результате структура отличается от предыдущей только тем, что длины отрезков разные. Однако отрезок длиной
─ волновое сопротивление линий, питающих порты. Для определения волновых сопротивлений отрезков TL3 и TL4 закоротим порт 1, питая МУ через порт 4. Полученная в результате структура отличается от предыдущей только тем, что длины отрезков разные. Однако отрезок длиной 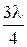 трансформирует сопротивление точно так же, как отрезок длиной
трансформирует сопротивление точно так же, как отрезок длиной 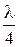 , и поэтому волновые сопротивления отрезков будут такими же, как у TL1 и TL2.
, и поэтому волновые сопротивления отрезков будут такими же, как у TL1 и TL2.
В заключение рассмотрим способы получения синфазных и противофазных сигналов. Если возбуждать порт 2, то на портах 1 и 3 будут синфазные сигналы, а при возбуждении порта 3 синфазные сигналы появятся на портах 2 и 4. Если возбуждать порт 4, то противофазные сигналы будут на портах 3 и 1, а при возбуждении порта 3 противофазные сигналы появятся на портах 1 и 4.
Дата добавления: 2017-11-04; просмотров: 3233;
