Стационарная теплопроводность через плоскую стенку.

1).Однородная плоская стенка (Рис.9.2.).

Температуры поверхностей стенки –t_ст1 и t_ст2.

Плотность теплового потока:

q = -λ∙ ∂t/∂n = - λ∙ ∂t/∂x = - λ∙ (t_cт2 - t_cт1)/(x_cт2 - x_cт1)∙

или

q = λ∙ (t_cт2 - t_cт1)/(x_cт2 - x_cт1)∙ Dt/Dx (9.13)

- температурный напор;

- толщина стенки.

Тогда

q = λ/δ∙(t_ст1 – t_ст2) = λ/δ∙Δt, (9.14)

Если R =δ/λ -термическое сопротивление теплопроводности стенки [(м²∙К)/Вт], то плотность теплового потока:

q = (t_ст1 – t_ст2)/R . (9.15)

Общее количество теплоты, которое передается через поверхность F за время τ определяется:

Q = q∙F∙τ = (t_ст1 – t_ст2)/R·F∙τ . (9.16)

Температура тела в точке с координатой х находится по формуле:

t_x = t_ст1 – (t_ст1 – t_ст2)∙x/ δ . (9.17)

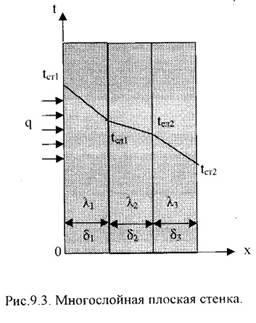
2).Многослойная плоская стенка.

Рассмотрим 3-х слойную стенку (Рис.9.3). Температура наружных поверхностей стенокt_ст1 и t_ст2, коэффициенты теплопроводности слоевλ₁, λ₂, λ₃, толщина слоевδ₁, δ₂, δ₃.

Плотности тепловых потокок через каждый слой стенки:

q = λ₁/δ₁∙(t_ст1 – t_сл1) , (9.18)

q = λ₂/δ₂∙(t_сл1 – t_сл2) , (9.19)

q = λ₃/δ₃∙(t_сл2 – t_ст2) , (9.20)

Решая эти уравнения, относительно разности температур и складывая, получаем:

q = (t₁ – t₄)/(δ₁/λ₁ + δ₂/λ₂ + δ₃/λ₃) = (t_ст1 – t_ст4)/R_o , (9.21)

где: R_o = (δ₁/λ₁ + δ₂/λ₂ + δ₃/λ₃) – общее термическое сопротивление теплопроводности многослойной стенки.

Температура слоев определяется по следующим формулам:

t_сл1 = t_ст1 – q∙(δ₁/λ₁). (9.22)

t_сл2 = t_сл1 – q·δ₂/λ₂). (9.23)

9.3. Стационарная теплопроводность через цилиндрическую стенку.

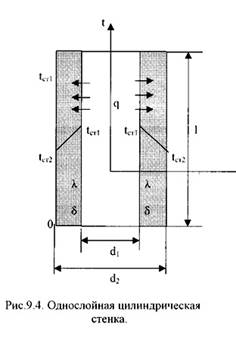
1). Однородная цилиндрическая стенка.

Рассмотрим однородный однослойный цилиндр длиной l, внутренним диаметром d₁и внешним диаметром d₂ (Рис.9.4).

Температуры поверхностей стенки –t_ст1 и t_ст2.

Уравнение теплопроводности по закону Фурье в цилиндрических координатах:

Q = - λ∙2∙π∙r ·l· ∂t / ∂r (9.24)

или

Q = 2·π·λ·l·Δt/ln(d₂/d₁), (9.25)

где: Δt = t_ст1 – t_ст2 – температурный напор;

λ – κоэффициент теплопроводности стенки.

Для цилиндрических поверхностей вводят понятия тепловой поток единицы длины цилиндрической поверхности (линейная плотность теплового потока), для которой расчетные формулы будут:

q_l = Q/l =2·π·λ·Δt /ln(d₂/d₁), [Вт/м]. (9.26)

Температура тела внутри стенки с координатойd_х:

t_x = t_ст1 – (t_ст1 – t_ст2) ·ln(d_x/d₁) / ln(d₂/d₁). (9.27)

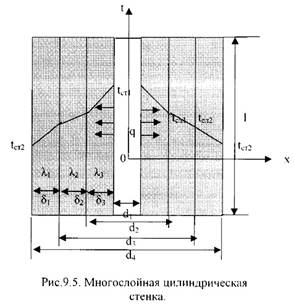
2). Многослойная цилиндрическая стенка.

Допустим цилиндрическая стенка состоит из трех плотно прилегающих слоев (Рис.9.5).

Температура внутренней поверхности стенки –t_ст1, температуранаружнойповерхности стенки –t_ст2, коэффициенты теплопроводности слоев -λ₁, λ₂, λ₃, диаметры слоев d₁, d₂, d₃, d₄.

Тепловые потоки для слоев будут:

1-й слой

Q = 2·π· λ₁·l·(t_ст1 – t_сл1)/ ln(d₂/d₁), (9.28)

2-й слой

Q = 2·π·λ₂·l·(t_сл1 – t_сл2)/ ln(d₃/d₂), (9.29)

3-й слой

Q = 2·π·λ₃·l·(t_сл2 – t_ст2)/ ln(d₄/d₃), (9.30)

Решая полученные уравнения, получаем для теплового потока через многослойную стенку:

Q = 2·π·l·(t_ст1 – t_ст2) / [ln(d₂/d₁)/λ₁ + ln(d₃/d₂)/λ₂ + ln(d₄/d₃)/λ₃]. (9.31)

Для линейной плотности теплового потока имеем:

q_l = Q/l = 2·π· (t₁ – t₂) / [ln(d₂/d₁)/λ₁ + ln(d₃/d₂)/λ₂ + ln(d₄/d₃)/λ₃]. (9.32)

Температуру между слоями находим из следующих уравнений:

t_сл1 = t_ст1 – q_l·ln(d₂/d₁) / 2·π·λ₁ . (9.33)

t_сл2 = t_сл1 – q_l·ln(d₃/d₂) / 2·π·λ₂ . (9.34)