Безударные принтеры. 3 страница
6. Массовость означает, что алгоритм решения задачи разрабатывается в общем виде, т. е. он должен быть применим для некоторого класса задач, различающихся лишь исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.
Величины и их характеристики
Величина – это основная единица для работы с информацией в информатике. Основными характеристиками величин являются имя, значение, вид и тип.
Конкретное обозначение величины называют именем. Имя величины состоит из одной или нескольких латинских букв, цифр, других знаков. Заглавные и строчные буквы в именах величин считаются одинаковыми, вначале всегда пишется буква.
Например: А, DR, t45, massa1.
Конкретное данное, которому равна величина в каждый момент времени, называют значением. Значение величины может быть представлено числом, каким-либо текстом или арифметическим выражением.
Например: 5, -12.89, "новость", "**,**", 5+45*a-b/3.
Запятая в десятичных дробях заменяется точкой.
Текст - это любой набор знаков, взятый в кавычки.
Знаки арифметического действия в значениях величин заменяются:
| Математика | Информатика | Пример |
| сложение | + | a + b => a + b |
| вычитание | - | a - b => a - b |
| умножение | * | a · b => a * b |
| деление | / | a : b => a / b |
| возведение в степень | ^ | a4 => a ^ 4 |
Виды величин
| Постоянные | Переменные |
| значения таких величин не меняются в процессе исполнения алгоритма | значения таких величин могут изменяться при выполнении алгоритма |
| 21.5; -1000; "ОИиВТ" | a; b14; summa8 |
Типы величин
| Тип | Значения величин | Примеры |
| целый | Значения целых величин - целые числа | 5; -100; 32 |
| вещественный | значения вещественных величин - действительные числа | 2.5; -31.78; a; b; 21+32*a |
| символьный (литерный или строковый) | значения символьных величин - набор символов (текст), взятый в кавычки. После имен символьных величин ставится знак $ (символьное). | "ШКОЛА"; "*!*"; A$ |
| логический | значений таких величин всего два: | true (истинно) false (ложно) |
| другие |
Команда присваивания
Величина получает свое значение путем выполнения команды присваивания. Она обозначается знаком «:=» (присвоить) и записывается следующим образом:
ИМЯ ВЕЛИЧИНЫ:=ЗНАЧЕНИЕ
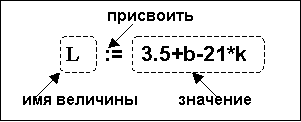
Например:
h:=12; g:="мотор"; tk1:=35*(41+s)^2.
Присвоение U:=d означает, что мы должны присвоить переменной U такое же значение, какое имеет величина d, при этом значение второй величины (d) не изменится.
Нельзя путать знак присваивания со знаком равенства, так, например, при выполнении следующей команды присваивания Z:=Z+1, величина Z станет равной предыдущему значению Z, увеличенному на 1.
Ясно, что использование в этой записи знака равенства недопустимо, т. к. никакое Z не равно Z+1.
Команда присваивания обладает следующими свойствами:
1) пока переменной не присвоено значения, она остается неопределенной;
2) значение, присвоенное переменной, сохраняется в ней вплоть до выполнения следующего присваивания этой переменной нового значения;
3) новое значение, присвоенное переменной, заменяет ее предыдущее значение.
После присваивания величине нового значения старое забывается.
Формы записи алгоритмов
На практике наиболее распространены следующие формы представления алгоритмов:
- словесная (запись на естественном языке);
- табличная (запись алгоритма в виде таблицы);
- графическая (изображения из графических символов);
- псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке, включающие в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.);
- программная (тексты на языках программирования).
Словесный способ записи алгоритмов
Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задается в произвольном изложении на естественном языке.
Словесный способ не имеет широкого распространения, т. к. такие описания:
- строго не формализуемы;
- страдают многословностью записей;
- допускают неоднозначность толкования отдельных предписаний.
Табличная форма записи алгоритмов
Используемые таблицы могут быть различными. Для примера будем использовать упрощенную форму.
Порядок составления табличных алгоритмов:
1. Переписать выражение так, как допустимо в информатике.
2. Определить порядок действий.
3. Ввести обозначения промежуточных результатов.
4. Занести полученные действия в таблицу.
Пример: алгоритм вычисления R=2a+3b.
| № действия | Действие | Величина | Результат | |
| * | a | k | ||
| * | b | u | ||
| + | k | u | R |
Графический способ записи алгоритмов
Графический способ представления алгоритмов является более компактным и наглядным по сравнению со словесным.
При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.
Такое графическое представление называется схемой алгоритма или блок-схемой. В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т. п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий. В таблице приведены наиболее часто употребляемые символы.
| Название символа | Обозначение и пример заполнения | Пояснение |
| Процесс | 
| Вычислительное действие или последовательность действий |
| Решение | 
| Проверка условий |
| Модификация | 
| Начало цикла |
| Предопределенный процесс | 
| Вычисления по подпрограмме, стандартной подпрограмме |
| Ввод-вывод | 
| Ввод-вывод в общем виде |
| Пуск-останов | 
| Начало, конец алгоритма, вход и выход в подпрограмму |
| Документ | 
| Вывод результатов на печать |
| Направление | 
| Последовательность выполнения действий: - влево и вверх – линия со стрелкой, - вниз и вправо – линия без стрелки |
Блок «процесс» применяется для обозначения действия или последовательности действий, изменяющих значение, форму представления или размещения данных. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Представление отдельных операций достаточно свободно.
Блок «решение» используется для обозначения переходов управления по условию. В каждом блоке «решение» должны быть указаны вопрос, условие или сравнение, которые он определяет.
Блок «модификация» используется для организации циклических конструкций. (Слово модификация означает видоизменение, преобразование). Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.
Блок «предопределенный процесс» используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.
 Блоки соединяются стрелками или линиями и показывают структуру всего алгоритма.
Блоки соединяются стрелками или линиями и показывают структуру всего алгоритма.
Алгоритм в виде блок-схемы начинается блоком «начало» и заканчивается блоком «конец».
При составлении блок-схемы алгоритма сначала выделяют исходные данные (все переменные величины после знака равенства и в условии) и результат (величины которые необходимо найти). Если в задании подразумеваются, но не указываются имена величин, то они обозначаются самостоятельно.
При отсутствии исходных данных блок ввода не пишется. В один блок можно поместить одно действие.
Пример: алгоритм вычисления значения выражения (ВЗВ) K=3b+6а.
Дано: b, a
Результат: K
K=3*b+6*a
1) R:=3*b
2) M:=6*a
3) K:=R+M
Псевдокод
Псевдокод представляет собой систему обозначений и правил, предназначенную для единообразной записи алгоритмов.
Псевдокод занимает промежуточное место между естественным и формальным языками. С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи.
В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя.
Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл которых определен раз и навсегда. Они выделяются в печатном тексте жирным шрифтом, а в рукописном тексте подчеркиваются.
Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций.
Базовые алгоритмические структуры
Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных базовых (т. е. основных) элементов. Естественно, что при таком подходе к алгоритмам изучение основных принципов их конструирования должно начинаться с изучения этих базовых элементов. Для их описания будем использовать язык схем алгоритмов и школьный алгоритмический язык.
Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: следование, ветвление, цикл.
Характерной особенностью базовых структур является наличие в них одного входа и одного выхода.
Базовая структура «следование»
Образуется последовательностью действий, следующих одно за другим:
| Алгоритмический язык | Язык блок-схем |
| действие 1 действие 2 . . . . . . . . . действие n | 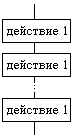
|
Алгоритм, в котором есть структура СЛЕДОВАНИЕ, называется ЛИНЕЙНЫМ. Следование - это расположение действий друг за другом.
Базовая структура «ветвление»
Обеспечивает в зависимости от результата проверки условия (да или нет) выбор одного из альтернативных путей работы алгоритма. Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран.
Условие представляет собой строку, содержащую операцию сравнения с использованием знаков <, >, =.
Например: x>5; s1<-15.5; d$="да"; j<>4 (не равно); Z3>=3 (больше или равно); t<=0 (меньше или равно).
Если условие соблюдается, то выполняются действия, расположенные в ветви под названием «Да». В случае несоблюдения условия будут выполнены действия, расположенные в ветви «Нет».
Структура ветвление существует в четырех основных вариантах:
- если – то;
- если – то – иначе;
- выбор;
- выбор – иначе.
Первый и третий варианты называются неполным ветвлением, второй и четвертый – полным. Неполная форма ветвления отличается от полной тем, что в одной из ветвей действия отсутствуют. В таком алгоритме в соответствии с условием либо будут выполнены действия, имеющиеся в ветви, либо начнут сразу выполняться действия, расположенные после ветвления.
| Алгоритмический язык | Язык блок-схем |
| 1. если – то | |
| если условие то действия все | 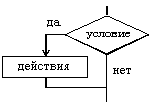
|
| 2. если – то – иначе | |
| если условие то действия 1 иначе действия 2 все | 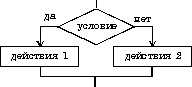
|
| 3. выбор | |
| выбор при условие 1: действия 1 при условие 2: действия 2 . . . . . . . . . . . . при условие N: действия N все | 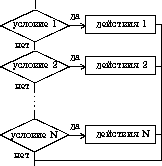
|
| 4. выбор – иначе | |
| выбор при условие 1: действия 1 при условие 2: действия 2 . . . . . . . . . . . . при условие N: действия N иначе действия N+1 все | 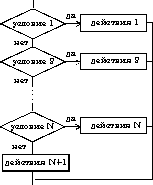
|
Алгоритм, в котором есть структура ВЕТВЛЕНИЕ, называется РАЗВЕТВЛЯЮЩИМСЯ. Ветвление - это выбор действия в зависимости от выполнения какого-нибудь условия.
Примеры структуры ветвление
| Алгоритмический язык | Язык блок-схем |
| если x>0 то y:=sin(x) все | 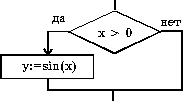
|
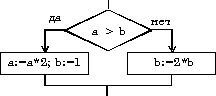
если 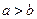 то
то 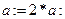 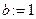 иначе
иначе 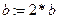 все
все
| 
|
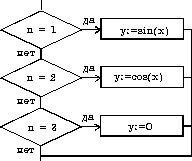
выбор
при 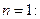 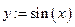 при
при 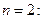 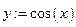 при
при 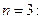 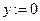 все
все
| 
|
| выбор при a>5: i:=i+1 при a=0: j:=j+1 иначе i:=10; j:=0 все | 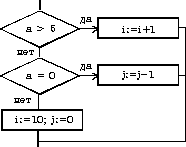
|
Базовая структура «цикл»
Обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла. Основные разновидности циклов представлены в таблице:
| Школьный алгоритмический язык | Язык блок-схем |
| Цикл Пока Предписывает выполнять тело цикла до тех пор, пока выполняется условие, записанное после слова пока. Цикл может не выполниться ни одного раза. | |
| нц пока условие тело цикла (последовательность действий) кц | 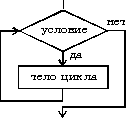
|
| Цикл До Тело цикла размещается до проверки условия его окончания. Цикл выполнится хотя бы один раз. | |
| нц до тело цикла (последовательность действий) условие кц | 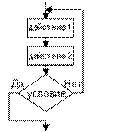
|
| Цикл Для (Спараметром). Предписывает выполнять тело цикла для всех значений некоторой переменной (параметра цикла) в заданном диапазоне. | |
| нц для i от i1 до i2 тело цикла (последовательность действий) кц | 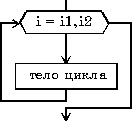
|
 Алгоритм, в котором есть структура ЦИКЛ, называется ЦИКЛИЧЕСКИМ. Цикл - это неоднократное повторение каких-либо действий. Структура ЦИКЛ используется при составлении алгоритмов, в которых необходимо многократно повторять какие-либо действия.
Алгоритм, в котором есть структура ЦИКЛ, называется ЦИКЛИЧЕСКИМ. Цикл - это неоднократное повторение каких-либо действий. Структура ЦИКЛ используется при составлении алгоритмов, в которых необходимо многократно повторять какие-либо действия.
Для организации цикла с параметром вводится величина (счетчик), которая меняет свое значение от начального до конечного с определенным шагом. Шаг равен разности между следующим и предыдущим значением величины.
Если при выполнении алгоритма должен получиться ряд ответов, то блок вывода помещается внутри цикла.
Например:
от Х=10 до 13 шаг 1 (Х будет принимать значения равные 10, 11, 12, 13);
от R=20 до 14 шаг -2 (R будет принимать значения равные 20, 18, 16, 14).
Все действия, размещенные внутри цикла, называются телом цикла. Тело цикла выполняется столько раз, сколько разных значений примет параметр в заданных пределах.
На алгоритмическом языке начало и конец цикла обозначают служебными словами нц и кц. Для организации цикла так же можно использовать блок логического условия.
Примеры структуры цикл
| Школьный алгоритмический язык | Язык блок-схем |
| нц пока i<=5 S:=S+A[i] i:=i+1 кц | 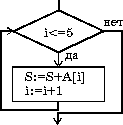
|
| N:=3 нц K:=N^2 вывод K N:=N+2 до N>5 кц | 
|
| нц для i от 1 до 5 X[i]:=i*i*i Y[i]:=X[i]/2 кц | 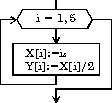
|
 Комбинированные алгоритмы
Комбинированные алгоритмы
Алгоритм, который содержит несколько структур одновременно, называется КОМБИНИРОВАННЫМ.
Рассмотрим пример комбинированного алгоритма.
Определите, какими блоками организованы структуры алгоритма.
Следование - 1-3, 5-6, 8-9, 10-11 блоки.
Ветвление - 4-9 блоки.
Цикл - 7-9 блоки.
ЯЗЫКИ ПРОГРАММИРОВАНИЯ
Программный способ записи алгоритмов
При записи алгоритма в словесной форме, в виде блок-схемы или на псевдокоде допускается определенный произвол при изображении команд. Вместе с тем такая запись точна настолько, что позволяет человеку понять суть дела и исполнить алгоритм.
Однако на практике в качестве исполнителей алгоритмов используются компьютеры. Поэтому алгоритм, предназначенный для исполнения на компьютере, должен быть записан на понятном ему языке. Здесь на первый план выдвигается необходимость точной записи команд, не оставляющей места для произвольного толкования их исполнителем.
Следовательно, язык для записи алгоритмов должен быть формализован. Такой язык принято называть языком программирования, а запись алгоритма на этом языке – программой.
Уровни языков программирования
В настоящее время в мире существует несколько сотен используемых языков программирования. Для каждого есть своя область применения.
Любой алгоритм есть последовательность предписаний, выполнив которые можно за конечное число шагов перейти от исходных данных к результату. В зависимости от степени детализации предписаний обычно определяется уровень языка программирования – чем меньше детализация, тем выше уровень языка. По этому критерию можно выделить следующие уровни языков программирования:
- машинные;
- машинно-ориентированные (ассемблеры);
- машинно-независимые (языки высокого уровня).
Машинные языки и машинно-ориентированные языки – это языки низкого уровня, требующие указания мелких деталей процесса обработки данных. Языки же высокого уровня имитируют естественные языки, используя некоторые слова разговорного языка и общепринятые математические символы. Эти языки более удобны для человека.
Языки высокого уровня делятся на:
- процедурные (алгоритмические) (Basic, Рascal, C и др.), которые предназначены для однозначного описания алгоритмов; для решения задачи процедурные языки требуют в той или иной форме явно записать процедуру ее решения;
- логические (Рrolog, Lisр и др.), которые ориентированы не на разработку алгоритма решения задачи, а на систематическое и формализованное описание задачи с тем, чтобы решение следовало из составленного описания;
- объектно-ориентированные (Object Рascal, C++, Java и др.), в основе которых лежит понятие объекта, сочетающего в себе данные и действия над нами. Программа на объектно-ориентированном языке, решая некоторую задачу, по сути, описывает часть мира, относящуюся к этой задаче. Описание действительности в форме системы взаимодействующих объектов естественнее, чем в форме взаимодействующих процедур.
Все сказанное выше можно представить в виде схемы – структурной классификации языков программирования. В ней указаны основные методологии программирования; в нижнем ряду, в скобках – типичные языки соответствующих групп.
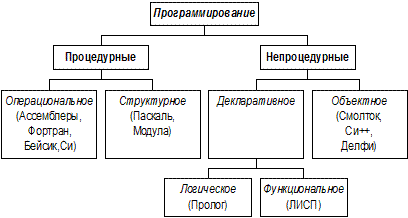
Язык ассемблера – это машинно-зависимый язык низкого уровня, в котором короткие мнемонические имена соответствуют отдельным машинным командам. Используется для представления в удобочитаемой форме программ, записанных в машинном коде.
Перевод программы с языка ассемблера на машинный язык осуществляется специальной программой, которая называется ассемблером и является, по сути, простейшим транслятором. Трансляторы переводят программу с языка программирования в машинные коды. Виды трансляторов: интерпретатор – построчный перевод и исполнение, компилятор – перевод всей программы с последующим исполнением.
Алгоритмический язык (как и любой другой язык) образуют три его составляющие: алфавит, синтаксис и семантика.
Алфавит – это фиксированный для данного языка набор основных символов, т. е. «букв алфавита», из которых должен состоять любой текст на этом языке – никакие другие символы в тексте не допускаются.
Синтаксис – это правила построения фраз, позволяющие определить, правильно или неправильно написана та или иная фраза. Точнее говоря, синтаксис языка представляет собой набор правил, устанавливающих, какие комбинации символов являются осмысленными предложениями на этом языке.
Семантика определяет смысловое значение предложений языка. Являясь системой правил истолкования отдельных языковых конструкций, семантика устанавливает, какие последовательности действий описываются теми или иными фразами языка и, в конечном итоге, какой алгоритм определен данным текстом на алгоритмическом языке.
Основными понятиями в алгоритмических языках обычно являются:
1. Имена (идентификаторы) – употребляются для обозначения объектов программы (переменных, массивов, функций и др.).
2. Операции. Типы операций:
- арифметические операции +, –, *, / и др.;
- логические операции и, или, не;
- операции отношения <, >, <=, >=, =, <>;
- операция сцепки (иначе, «присоединения», «конкатенации») символьных значений друг с другом с образованием одной длинной строки; изображается знаком «+».
3. Данные – величины, обрабатываемые программой. Имеется три основных вида данных: константы, переменные и массивы.
- Константы – это данные, которые зафиксированы в тексте программы и не изменяются в процессе ее выполнения. Примеры констант:
а) числовые 7.5, 12;
б) логические да (истина), нет (ложь);
в) символьные (содержат ровно один символ) "А", "+";
г) литерные (содержат произвольное количество символов) "a0", "Мир", "" (пустая строка).
- Переменные обозначаются именами и могут изменять свои значения в ходе выполнения программы. Переменные бывают целые, вещественные, логические, символьные и литерные.
- Массивы – последовательности однотипных элементов, число которых фиксировано и которым присвоено одно имя. Положение элемента в массиве однозначно определяется его индексами (одним, в случае одномерного массива, или несколькими, если массив многомерный). Иногда массивы называют таблицами.
4. Выражения – предназначаются для выполнения необходимых вычислений, состоят из констант, переменных, указателей функций (например, exр(x)), объединенных знаками операций.
Выражения записываются в виде линейных последовательностей символов (без подстрочных и надстрочных символов, «многоэтажных» дробей и т. д.), что позволяет вводить их в компьютер, последовательно нажимая на соответствующие клавиши клавиатуры.
Различают выражения арифметические, логические и строковые.
- Арифметические выражения служат для определения одного числового значения. Например, (1+sin(x))/2. Значение этого выражения при x=0 равно 0.5, а при x=р/2 – единице.
- Логические выражения описывают некоторые условия, которые могут удовлетворяться или не удовлетворяться. Таким образом, логическое выражение может принимать только два значения – "истина" или "ложь" (да или нет). Рассмотрим в качестве примера логическое выражение x*x+y*y<r*r, определяющее принадлежность точки с координатами (x,y) внутренней области круга радиусом r c центром в начале координат. При x=1, y=1, r=2 значение этого выражения – "истина", а при x=2, y=2, r=1 – "ложь".
- Строковые (литерные) выражения, значениями которых являются тексты. В строковые выражения могут входить литерные и строковые константы, литерные и строковые переменные, литерные функции, разделенные знаками операции сцепки. Например, А+В означает присоединение строки В к концу строки А. Если А="куст ", а В="зеленый", то значение выражения А+В есть "куст зеленый".
5. Операторы (команды). Оператор – это наиболее крупное и содержательное понятие языка: каждый оператор представляет собой законченную фразу языка и определяет некоторый вполне законченный этап обработки данных. В состав операторов входят: ключевые слова, данные, выражения и т. д.
Дата добавления: 2017-11-04; просмотров: 534;
