поддерживается меняющаяся с течением времени температура

Задача сводится к решению уравнения (1.193) при граничных условиях

, ,

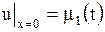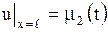(1.204)

и начальном условии

,

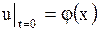(1.205)

где 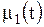, , 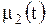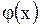- заданные функции. Будем искать решение этой задачи в виде ряда Фурье по собственным функциям (1.201)

,

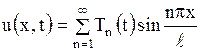(1.206)

где

,

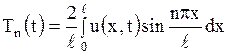(1.207)

считая при этом 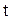параметром. Возьмем этот интеграл по частям дважды:

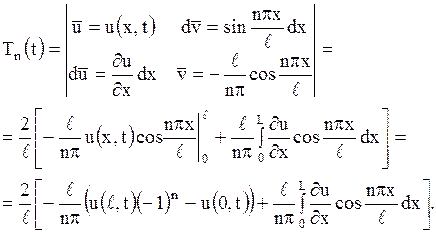
Последний интеграл берем по частям, положив 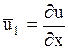, 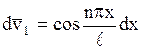. Тогда , .

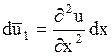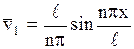Поэтому имеем

.

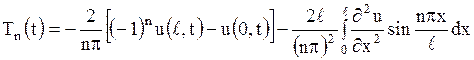Так как 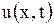удовлетворяет уравнению (1.193) и граничным условиям (1.204), то

.

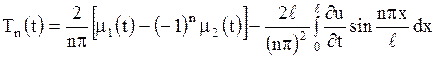(1.208)

Дифференцируя теперь выражение (1.207) по 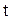, найдем

.

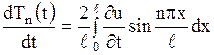(1.209)

Исключая интеграл из равенства (1.208) и (1.209), получим следующее уравнение для определения коэффициентов 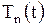разложения (1.206):

.

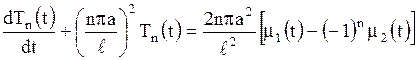(1.210)

Решим это уравнение методом вариации произвольной постоянной

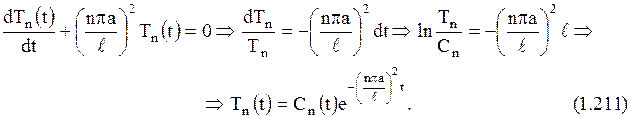
Тогда

.

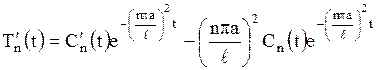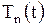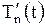Подставляя найденные выражения и в линейное неоднородное уравнение (1.210), получим дифференциальное уравнение относительно :

,

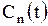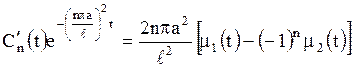откуда

.

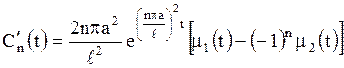Интегрируя, находим

.

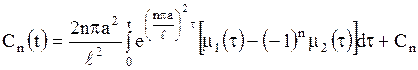Таким образом, общее решение уравнения (1.210) имеет вид

.

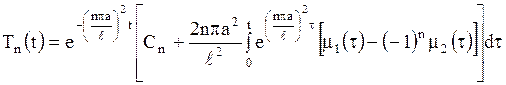(1.212)

Определим постоянные 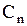. Очевидно, .

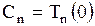Чтобы удовлетворить начальному условию (1.205), потребуем выполнения равенства

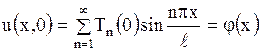
и, следовательно,

.

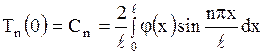(1.213)

Итак, решением задачи (1.193), (1.204) – (1.205) является ряд (1.206), в котором функции 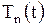определяется равенствами (1.212) и (1.213).