Методы корреляционно-регрессионного анализа фондового рынка. 1 страница

С помощью регрессионного анализа строится и проверяется мо­дель связи между одной зависимой (т.е. эндогенной) и одной или более независимыми (экзогенными) переменными. Зависи­мая переменная обычно обозначается Y, а независимая (ые), также называемая регрессором, - X.

Направление причинной связи между переменными опреде­ляется через предварительное обоснование и включается в модель как гипотеза. Регрессионный анализ проверяет статистическую состоятельность модели при данной гипотезе.

Например, предположим, выдвинута гипотеза о том, что уро­вень фондового индекса FТSЕ (FТSЕ 100) линейно зависит от уровня фондового индекса S&Р 500, т.е., когда растет S&Р 500, растет и FТSЕ 100, а когда S&Р 500 падает, падает и FТSЕ 100. Можно проверить эту гипотезу, используя простую линейную регрессию с включением только двух переменных.

Альтернативной гипотезой может быть то, что индекс FТSЕ 100 находится под влиянием не одного фактора, а нескольких. Напри­мер, на текущий уровень FТSЕ 100 могут влиять индекс S&Р 500, уровень рынка облигаций Великобритании и обменный курс $/£. Эта гипотеза может быть проверена с помощью множественной регрессии.

3.1. Простая линейная регрессия.

Применим регрессионный анализ для простой линейной зави­симости между зависимой переменной (Y) и одной независимой переменной (X).

Под линейностью мы имеем в виду, что переменная Y предположительно находится под влиянием переменной X в следую­щей зависимости:

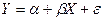, (3.1)

где

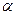- постоянная, т.е. если бы даже X была равна нулю, Y имела бы какое-либо положительное или отрицательное значение. Можно ли дать разумное объяснение значению Y даже при X равном нулю? Все зависит от гипо­тезы, для которой применяется регрессионный анализ.

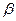- коэффициент регрессии, отражает наклон линии, вдоль которой рассеяны данные наблюдений. Он может быть истолкован как показатель, характеризующий процент­ное изменение переменной Y, которое вызвано измене­нием значения X на единицу. Таким образом, если Y и X - это соответственно индексы FТSЕ 100 и S&Р500, то 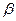будет указывать, на какое количество пунктов изме­нится FТSЕ 100 при изменении индекса S&Р 500 на один пункт. Если знак 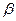положителен, то переменные положительно коррелированы. При отрицательном зна­ке 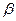переменные отрицательно коррелированны;

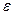- ошибка или значение помехи, также называемая остат­ком. Она отражает тот факт, что обычно движение Y бу­дет, по крайней мере, неточно описываться лишь движе­нием X. Присутствуют другие факторы, не включенные в данную модель. Однако если исследуемая гипотеза реалистична, то эти другие переменные должны быть относительно неважными.

Обращаясь снова к взаимосвязи между FТSЕ 100 и S&Р 500, отметим, что индекс FТSЕ 100 - зависимая переменная Y, так как мы выдвинули гипотезу о том, что движение этого индекса нахо­дится под влиянием, т.е. зависит от изменения индекса S&Р 500, который представлен переменной X. В данной гипотезе мы предполагаем, что множество других незначительных и неучтенных влияний представлены в модели величиной .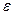

Если экономические аргументы достаточно сильны, мы мо­жем развить гипотезу о том, что уровень индекса S&Р 500 нахо­дится под влиянием индекса FТSЕ 100. При таком допущении величина индекса S&Р 500 стала бы переменной Y, а индекса FТSЕ 100 - переменой X.

Расположив данные из табл. 3.1 на приведенной ниже точечной диаграмме рассеяния (рис. 3.1), мы действительно видим, что высо­кие (низкие) значения S&Р 500 соответствуют высоким (низким) значениям РТ8Е 100. Таким образом, создается впечатление, что данные по двум индексам растут и падают вместе.

Таблица 3.1

Пример построения линейной регрессии.

FТSЕ 100 (Y)	S&Р 500 (X)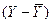
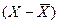
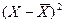
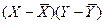
2851,6	442,52	-114,545	-10,726	115,0471	1228,61
2882,6	442,01	-83,545	-11,236	126,2477	938,7116
2878,4	450,3	-87,745	-2,946	8,678916	258,4968
2813,4	442,46	-152,745	-10,786	116,3378	1647,508
2849,2	453,83	-116,945	0,584	0,341056	-68,2959
2888,8	449,02	-77,345	-4,226	17,85908	326,86
2941,7	450,15	-24,445	-3,096	9,585216	75,68172
	463,15	118,855	9,904	98,08922	1177,14
3039,3	461,28	73,155	8,034	64,54516	587,7273
3164,4	469,1	198,255	15,854	251,3493	3143,135
3233,2	461,89	267,055	8,644	74,71874	2308,423
= 2966,14	= 453,25
Сумма:				882,7993

Однако фактические данные не говорят нам ничего о причинной связи. Наше понимание причинной связи исходит из предварительно выдвинутой гипотезы. Как мы заметили в одном из предыдущих абзацев, указание на причину и следствие, т.е. на то, что является зависимой, а что независимой переменной, оп­ределяется выдвинутой гипотезой.

Для иллюстрации этого вернемся снова к гипотезе о том, что уровень FТSЕ 100 находится под влиянием уровня S&Р 500. Фак­тические данные подтверждают эту идею, но поддержит ли ее наше понимание экономики финансов? S&Р 500 может влиять на FТSЕ 100 из-за огромного масштаба экономики США и меж­дународного оборота капитала. Однако альтернативное предпо­ложение заключается в том, что, так как оба рынка открыты для международных инвесторов, они оба могут находиться под влия­нием третьего фактора, может быть, ожидания японских или ев­ропейских инвесторов.

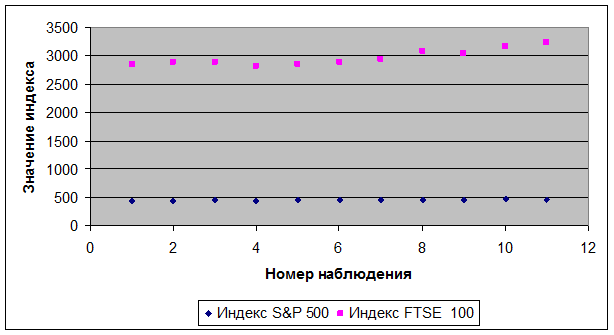Рис. 3.1. Динамика индексов FТSЕ 100 и S&Р 500.

Ясно, что независимо от регрессионной модели необходимо развивать гипотезу для того, чтобы регрессионный анализ смог обоснованно подтвердить или не подтвердить ее. Регрессионный анализ не в состоянии "доказать" гипотезу, он может лишь под­твердить ее статистически или отвергнуть.

Обращаясь к диаграмме рассеяния (рис. 3.1), отметим, что через точки на графике можно провести несколько прямых ли­ний, удовлетворяющих выражению (3.1), хотя в действительно­сти невозможно построить одну прямую линию, которая прой­дет через все точки корреляционного поля. Отсюда очевидно, что нужно выбрать лишь одну линию.

3.1.1. Определение параметров уравнения регрессии с помощью метода наименьших квадратов.

Для статистической проверки взаимосвязи между зависимой и независимой переменными необходимо найти значения 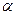, 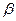и 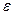в выражении (3.1). Метод оценки должен быть таким, чтобы это были наилучшие, линейные, несмещенные оценки (BLUE - Best, Linear, Unbiased Estimator).

Понятие наилучшие относится к требованию для оценок па­раметров быть наиболее эффективными, т.е., чтобы дисперсии оценок параметров были как можно меньше. Это достигается таким выбором значени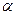й и 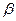, которые минимизируют сумму квадратов значений .

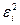Начальным пунктом эконометрического анализа зависимостей обычно является оценка линейной зависимости переменных. Если имеется некоторое "облако" точек наблюдений, через него всегда можно попытаться провести такую прямую линию, которая являет­ся наилучшей в определенном смысле среди всех прямых линий, то есть "ближайшей" к точкам наблюдений по их совокупности. Для этого мы вначале должны определить понятие близости прямой к некоторому множеству точек на плоскости; меры такой близости могут быть различными. Обычно в качестве критерия близости используется минимум суммы квадратов разностей наблюдений зависимой переменной 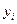и теоретических, рассчитанных по уравнению регрессии значений:

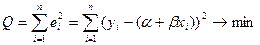(3.2).

Здесь считается, что 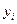и - и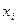звестные данные наблюдений, 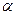и b - неизвестные параметры линии регрессии. Поскольку функция Q непрерывна, выпукла и ограничена снизу нулем, она имеет мини­мум. Для соответствующих точке этого минимума значени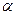й и 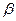могут быть найдены простые и удобные формулы (они будут приведены ниже). Метод оценивания параметров линейной регрессии, минимизирующий сумму квадратов отклонений наблюдений зави­симой переменной от искомой линейной функции, называется Ме­тодом наименьших квадратов (МНК).

"Наилучшая" по МНК прямая линия всегда существует, но даже наилучшая не всегда является достаточно хорошей. Если в действи­тельности зависимость у = f(х) является, например, квадратичной, то ее не сможет адекватно описать никакая линейная функция, хотя среди всех таких функций обязательно найдется "наилучшая". Если величины х и у вообще не связаны, мы также всегда сможем найти "наилучшую" линей­ную функцию у = а+bх для данной совокупности наблюдений, но в этом случае конкретные значения а и b определяются только случайными отклонениями переменных и сами будут очень сильно меняться для различных выборок из одной и той же генеральной совокупности.

Рассмотрим теперь задачу оценки коэффициентов парной ли­нейной регрессии более формально. Предположим, что связь между х и у линейна: у = 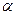+ 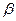х. Здесь имеется в виду связь между всеми возможными значениями величин х и у, то есть для генеральной совокупности. Наличие случайных отклонений, вызванных воздей­ствием на переменную у множества других, неучтенных в нашем уравнении факторов и ошибок измерения, приведет к тому, что связь наблюдаемых величин х и у приобретет вид (3.1). Задача состоит в следующем: по имеющимся данным наблюдений {х}, {у} оценить значения параметров 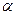и 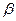, обеспечивающие минимум ве­личины Q.

Для оценки параметров 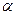и 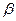воспользуемся МНК, который минимизирует сумму квадратов отклонений фактических значений 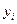от расчетных. Для этого необходимо найти производные по 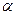и 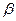от функции Q (уравнение 3.2) и приравнять их к нулю. Полученная система двух уравнений с двумя неизвестными позволяет найти значения коэффициентов 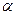и :

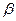(3.3).

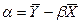(3.4).

При использовании МНК к ошибкам 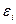предъявляются сле­дующие требования, называемые условиями Гаусса - Маркова:

1) величина 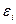является случайной переменной;

2) математическое ожидание 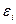равно нулю: М( 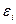) = 0;

3) дисперсия 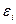постоянна: D( 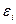) = 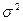для всех i;

4) значения 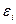независимы между собой. Откуда вытекает, в
частности, что

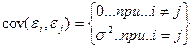
5) величины 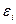статистически независимы от значений .

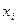Известно, что, если условия 1) - 5) выполняются, то оценки, сделанные с помощью МНК, обладают следующими свойствами:

1) Оценки являются несмещенными, т.е. математическое ожи­дание оценки каждого параметра равно его истинному значению: М( 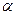)=а; М( 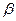)=b. Это вытекает из второго условия Гаусса-Маркова
и говорит об отсутствии систематической ошибки в определении положения линии регрессии.

2) Оценки состоятельны, так как дисперсия оценок парамет­ров при возрастании числа наблюдений стремится к нулю. Иначе говоря, если n достаточно велико, то практически наверняка 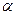близко к а и 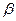близко к b: надежность оценки при увеличении выборки растет.

3) Оценки эффективны, они имеют наименьшую диспер­сию по сравнению с любыми другими оценками данного параметра, линейными относительно величин .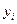

Перечисленные свойства не зависят от конкретного вида рас­пределения величин 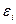, тем не менее, обычно предполагается, что они распределены нормально N(0; 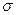²). Эта предпосылка необ­ходима для проверки статистической значимости сделанных оце­нок и определения для них доверительных интервалов. При ее выполнении оценки МНК имеют наименьшую дисперсию не только среди линейных, но среди всех несмещенных оценок.

Если предположения 3) и 4) нарушены, то есть дисперсия возмущений непостоянна и/или значения 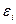связаны друг с дру­гом, то свойства несмещенности и состоятельности сохраняют­ся, но свойство эффективности - нет.

При невыполнении предположения 5) может нарушаться и свойство несмещенности оценок, являющееся наиболее важным в эконометрическом анализе.

3.1.2. Критерии значимости коэффициентов 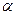и 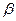в уравнении регрессии.

Формально значимость оцененного коэффициента регрессии 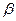может быть проверена с помощью анализа его отношения к своему стандартному отклонению 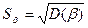. Эта величина в случае вы­полнения исходных предпосылок модели имеет t-распределение Стьюдента с (n-2) степенями свободы (n - число наблюдений). Она называется t-статистикой:

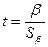(3.5).

Для t-статистики проверяется нулевая гипотеза, то есть гипотеза о равенстве ее нулю. Очевидно, t=0 равнозначно 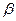=0, поскольку t пропорциональна 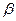. Аналогично проверяется значимость коэффициента .

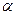При оценке значимости коэффициента линейной регрессии можно использовать следующее грубое правило. Если стандартная ошибка коэффициента больше его модуля, т.е. t < 1, то он не может быть признан хорошим (значимым). Если стандартная ошибка мень­ше модуля коэффициента, но больше его половины, т.е. 1 < t < 2, то сделанная оценка может рассматриваться как более или менее зна­чимая. Доверительная вероятность здесь примерно от 0,7 до 0,95. Значение tот 2 до 3 свидетельствуете весьма значимой связи (доверительная вероятность от 0,95 до 0,99), и t > 3 есть практически стопроцентное свидетельство ее наличия. Конечно, в каждом случае играет роль число наблюдений; чем их больше, тем надежнее при прочих равных условиях выводы о наличии связи и тем меньше верхняя граница доверительного интервала для данных числа степеней сво­боды и уровня значимости.

Коэффициент детерминации .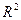

Регрессионная модель показывает, что вариация Y может быть объяснена вариацией независимой переменной X и значением ошибки 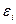. Очень часто необходимо знать, насколько вариация Y обусловлена изменением X и насколько она является следствием случайных причин. Другими словами, нам нужно знать, насколько хорошо рассчитанное уравнение регрессии соответствует фактическим данным, т.е. насколько мала вариация данных вокруг линии рег­рессии. Для оценки степени соответствия линии регрессии нам нужно рассчитать общую сумму квадратов отклонений, сумму квадратов отклонений, объясняемую регрессией, и остаточную сумму квадратов отклонений, чтобы определить коэффициент детерминации .

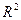Для анализа общего качества оцененной линейной регрессии ис­пользуют обычно коэффициент детерминации 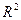, называемый так­же квадратом коэффициента множественной корреляции. Для слу­чая парной регрессии это квадрат коэффициента корреляции пере­менных X и Y. Коэффициент детерминации рассчитывается по фор­муле:

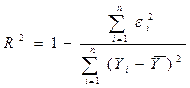(3.6).

В случае простой регрессии двух переменных R² представляет собой квадрат коэффициента корреляции.

Этот коэффициент характеризует долю вариации (разброса) зависимой перемен­ной, объясненной с помощью данного уравнения. В качестве меры разброса зависимой переменной обычно используется ее дисперсия, а остаточная вариация может быть измерена как дисперсия откло­нений вокруг линии регрессии. Если числитель и знаменатель вы­читаемой из единицы дроби разделить на число наблюдений n, то получим, соответственно, выборочные оценки остаточной диспер­сии и дисперсии зависимой переменной Y. Отношение остаточной и общей дисперсий представляет собой долю необъясненной диспер­сии. Если же эту долю вычесть из единицы, то получим долю дисперсии зависимой переменной, объясненной с помощью регрес­сии.

Иногда при расчете коэффициента детерминации для получе­ния несмещенных оценок дисперсии в числителе и знаменателе вы­читаемой из единицы дроби делается поправка на число степеней свободы; тогда

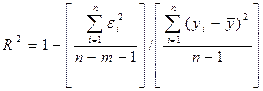(3.7)

или, для парной регрессии, где число независимых переменных nравно 1:

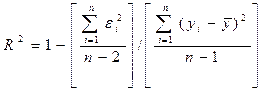(3.8).

Обычный 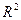(без поправки) всегда растет при добавлении новой переменной; в 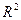с поправкой растет величина т, уменьшающая его. Если увеличение доли объясненной дисперсии при добавлении новой переменной мало, то 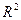с поправкой может уменьшиться. Если это так, то добавлять переменную нецелесообразно. Скорректированный R² уменьшится по величине, если до­полнительная переменная незначима. Однако необходимо пре­достеречь против включения и исключения переменных только лишь из-за их влияния на скорректированный R². Рациональной базой для включения и исключения служит экономическая теория, стоящая за проверяемой моделью. Отсюда переменная, которая имеет сильное теоретическое основание для включения, должна быть до­бавлена в модель, даже если скорректированный R² от этого не улучшится.

Если существует статистически значимая линейная связь вели­чин X и Y, то коэффициент 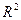близок к единице. Однако он может быть близким к единице просто в силу того, что обе эти величины имеют выраженный временной тренд, не связанный с их причин­но-следственной взаимозависимостью. В экономике обычно объем­ные показатели (доход, потребление, инвестиции) имеют такой тренд, а темповые и относительные (производительности, темпы роста, доли, отношения) - не всегда. Поэтому при оценивании линейных рег­рессий по временным рядам объемных показателей (например, за­висимости выпуска от затрат ресурсов или объема потребления от величины дохода) величина 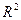обычно очень близка к единице. Это, говорит о том, что зависимую переменную нельзя описать просто как равную своему среднему значению, но это и заранее очевидно, раз она имеет временной тренд.

Если имеются не временные ряды, а перекрестная выборка, то есть данные об однотипных объектах в один и тот же момент вре­мени, то для оцененного по ним уравнения линейной регрессии величина 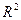не превышает обычно уровня 0.6 - 0.7. То же самое обычно имеет место и для регрессии по временным рядам, если они не имеют выраженного тренда. В макроэкономике примерами та­ких зависимостей являются связи относительных, удельных, тем­повых показателей: зависимость темпа инфляции от уровня безра­ботицы, нормы накопления от величины процентной ставки, темпа прироста выпуска от темпов прироста затрат ресурсов. Таким обра­зом, при построении макроэкономических моделей, особенно - по временным рядам данных, нужно учитывать, являются входящие в них переменные объемными или относительными, имеют ли они временной тренд.

Для определения статистической значимости коэффициента детерминации 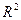проверяется нулевая гипотеза для F-статистики, рассчитываемой по формуле:

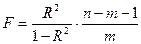(3.9).

Соответственно, для парной регрессии . Смысл проверяемой гипотезы заключается в том, что все коэффициенты линейной регрессии, за исключением свободного члена, равны нулю. Если они действительно равны нулю для генеральной совокупнос­ти, то уравнение регрессии должно иметь вид 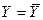, а коэффициент детерминации 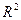и F-статистика Фишера также равны нулю. При этом их оценки для случайной выборки, конечно, отличаются от нуля, но чем больше такое отличие, тем менее оно вероятно. Логика проверки нулевой гипотезы заключается в том, что если произошло событие, которое было бы слишком маловероятным в том случае, если данная гипотеза действительно была бы верна, то эта гипотеза отвергается.

Величина F,если предположить, что выполнены предпосылки относительно отклонений 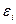,имеет распределение Фишера с (m; n-m-1) степенями свободы, где m - число объясняющих переменных, n - число наблюдений. Распределение Фишера - двухпараметрическое распределение неотрицательной случайной величины, являю­щейся в частном случае, при m=1,квадратом случайной величины, распределенной по Стьюденту. Для распределения Фишера имеют­ся таблицы критических значений, зависящих от чисел степеней свободы mи n-m-1,при различных уровнях значимости.

Итак, показатели F и 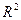равны или не равны нулю одновремен­но, поэтому F = 0 равнозначно тому, что линия регрессии 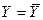является наилучшей по МНК и, следовательно, величина Y статис­тически независима от X. Поэтому проверяется нулевая гипотеза для показателя F, который имеет хорошо известное, табулированное распределение Фишера. Для проверки этой гипоте­зы при заданном уровне значимости по таблицам находится крити­ческое значение 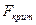- и нулевая гипотеза отвергается, если F > 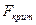. Пусть, например, при оценке парной регрессии по 15 наблюдениям 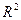= 0.7. В этом случае 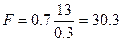. По таблицам для распределения Фишера с (1; 13) степенями свободы найдем, что при 5%-ном уровне значимости (доверительная вероятность 95%) кри­тическое значение F равно 4.67, при 1%-ном – 9.07. Таким образом, для того, чтобы отвергнуть гипотезу о равенстве нулю одновременно всех коэффи­циентов линейной регрессии, коэффициент детерминации не до­лжен быть очень близким к единице; его критическое значение для данного числа степеней свободы уменьшается при росте числа на­блюдений и может стать сколь угодно малым. В то же время вели­чина коэффициента 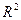может служить отражением общего качест­ва регрессионной модели.