Графическое представление и первичная обработка фондовых данных.
1.1. Общие сведения.
Термин «первичные данные» - это общий термин, относящийся к группе сводных показателей, каждый из которых одним числом определяет какое-либо качество совокупности данных. Например, при анализе рынка ценных бумаг часто необходимо подсчитать некоторую форму среднего значения группы активов или среднюю цену активов в данном периоде. Также финансовым аналитикам часто приходится измерять, как рассеяны доходности и цены фондовых инструментов. На практике часто требуется узнать, как распределены доходности и цены симметрично вокруг средней величины, имеется ли скошенность в распределении доходов и имеет ли их распределение пик, выраженный больше или меньше, чем предполагалось.
Статистики определяют средние значения как показатели центра распределения. Статистические показатели, которые описывают или измеряют, как данные распределены вокруг среднего значения, известны как показатели вариации. Величины, определяющие симметричность данных, называются показателями асимметрии или мерами скошенности, а выражающие пиковость данных - показателями эксцесса.
Данные могут иметь различный вид, который иногда диктует выбор методов статистического анализа или, по меньшей мере, влияет на него. Таким образом, до начала изучения различных методов статистического анализа следует рассмотреть различные виды данных.
Непрерывные и дискретные данные.
Данные могут быть классифицированы как непрерывные и дискретные. Непрерывные данные могут принимать любые значения на множестве действительных чисел, т.е. они измеряются на непрерывной шкале, а их значения ограничены только степенью точности. Типичным примером является процентная ставка дохода по инвестициям. Она может составлять 12%, 12,3% или вообще 12,0675%. Данные, относящиеся ко времени, расстоянию и скорости, также попадают в эту категорию.
Дискретные данные связаны с процессом счета. Например, число финансовых сделок дискретно, потому что их половины или четверти не имеют рационального смысла. Данные, связанные с ценами активов, могут быть дискретными из-за установленных на индивидуальных рынках правил котировки и минимальных ценовых изменений. Например, в Великобритании государственные облигации котируются в тридцать вторых (1/32) долях фунта. Следовательно, ценовые данные здесь дискретны и изменяются только в тридцать вторых долях или кратных им значениях. Рынки корпоративных облигаций, акций, фьючерсов и опционов служат другими примерами, где правила минимальных ценовых изменений определяют дискретность данных.
Данные кросс-секций ивременных рядов.
Кросс-секционные (cross-sectional)данные представляют собой информацию в группе переменных в каждый отдельный момент времени. Например, данные, связанные с ценами акций каждой из входящих в расчет, например, индекса FTSE 100 в конкретный момент времени, являются кросс-секционными. Списки цен акций, процентных ставок или обменных курсов, публикуемые в деловых разделах газет, также представляют собой кросс-секционные данные, потому что относятся к ценам или ставкам нескольких переменных (акций, валют и т. п.) в данный момент времени.
Временные ряды отражают колебания какой-либо переменной на промежутке времени. Например, данные о цене акции, обменном курсе валюты или уровне индекса за каждый день (неделю или месяц) в течение некоторого интервала времени будут ежедневным (еженедельным или ежемесячным) временным рядом. Временной ряд - этопоследовательность упорядоченных во времени числовых показателей,характеризующих уровень
Всякий временной ряд включает два обязательных элемента: во-первых, время и, во-вторых, конкретное значение показателя, или уровень ряда. Временные ряды различаются по следующим признакам:
1) по времени - моментные и интервальные. Интервальный ряд - последовательность, в которой уровень явления относят к результату, накопленному или вновь произведенному за определенный интервал времени. Таковы, например, ряды показателей объема продукции предприятия по месяцам года, количества отработанных человеко-дней по отдельным периодам (месяцам, кварталам, полугодиям, годам, пятилетиям и т.п.) и т.д. Если же уровень ряда характеризует изучаемое явление в конкретный момент времени, то совокупность уровней образует моментами ряд. Примерами моментных рядов могут быть последовательность показателей численности населения на начало года, поголовье скота в фермерских хозяйствах на 1 сентября и т.д. Важное отличие моментных рядов от интервальных состоит в том, что сумма уровней интервального ряда дает вполне реальный показатель – общий выпуск продукции за год (пятилетие, десятилетие), общие затраты рабочего времени, общин объем продаж акций и т.д., сумма же уровней моментного ряда иногда и подсчитывается, но реального содержания, как правило, не имеет;
2) по форме представления уровней – ряды абсолютных, относительных и средних величин;
3) по расстоянию между датами или интервалами времени выделяют полные и неполные временные ряды. Полные ряды имеют место, когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами, неполные - когда принцип равных интервалов не соблюдается;
4) по содержанию показателей - ряды частных и агрегированных показателей. Частные показатели характеризуют изучаемое явление односторонне, изолированно. Например, среднесуточный объем выпуска промышленной продукции дает возможность оцепить динамику промышленного производства, численность граждан, состоящих на учете в службе занятости;
показывает эффективность социальной политики государства;
остатки наличных денег у населения и вклады населения в банках отражают платежеспособность населения и т.д. Агрегированные показатели основаны на частных показателях и характеризуют изучаемый процесс комплексно. Так, чтобы иметь представление о состоянии фондового рынка России в целом, необходимо определять агрегированный показатель экономической конъюнктуры, включающий в себя и вышеперечисленные частные показатели. Широкое применение агрегированных показателей стало возможным с развитием факторного и компонентного анализа.
Важнейшим условием правильного формирования временных рядов является сопоставимость уровней, образующих ряд. Уровни ряда, подлежащие изучению, должны быть однородны по экономическому содержанию, учитывать существо изучаемого явления и цель исследования.
Статистические данные, представленные в виде временных рядов, должны быть сопоставимы по территории, кругу охватываемых объектов, единицам измерения, моменту регистрации, методике расчета, ценам, достоверности.
Несопоставимость по территории возникает в результате изменений границ стран, регионов, хозяйств и т.п. Для приведения данных к сравнимому виду производится пересчет прежних данных с учетом новых границ.
Полнота охвата различных частей явления - важнейшее условие сопоставимости уровней ряда.
Познание закономерностей изменения фондовых переменных во времени – сложная и трудоемкая процедура исследования, так как любое изучаемое явление формирует множество факторов, действующих в разных направлениях. По характеру непосредственного воздействия эти факторы могут быть разделены на две группы. К первой группе относятся факторы, определяющие основную тенденцию динамики (рост или снижение уровнен). Вторая группа факторов, вызывающая случайные колебания, отклоняет уровни от тенденции то в одном, то в другом направлении. Например, тенденция динамики объемов продаж ценных бумаг на фондовой бирже связана с укреплением экономики страны, с прогрессом развития информационных каналов связи, с совершенствованием организации и управления производством тех предприятий, чьи ценные бумаги представлены на рынке. Колеблемость динамики вызвана влиянием, например, мирового фондового рынка, неустойчивостью валютного курса и цен на сырье, неожиданными политическими решениями экономических вопросов.
При статистическом изучении динамики необходимо четко разделять два основных ее элемента - тенденцию и колеблемость, чтобы дать каждому из них количественную характеристику с помощью специальных показателей.
Основной тенденцией, или трендом, называется характеристика процесса изменения явления за длительное время, освобожденная от случайных колебаний, создаваемых второй группой факторов. В отличие от тенденции колеблемостью следует называть отклонения уровней отдельных периодов времени от тенденции динамики (тренда).
Сгруппированные и несгруппированные данные.
Только когда обрабатывается небольшое количество исходных данных, они могут быть оставлены в необработанном или несгруппированномвиде, при этом знакомящиеся с ними будут в состоянии их усвоить. Понятно, что когда набор данных велик, необходимо изложить его в виде таблицы для лучшего восприятия. Данные в таблице могут разбиваться на группы и объединяться в интервалы. Пример сгруппированных непрерывных данных показан в табл. 1.1.
Таблица 1.1
Представление сгруппированных данных.
| Месячный доход | Число наблюдений | Относительная частота |
| До -8% | ||
| Более -8% и до -7% | 0,039216 | |
| Более-7% и до -6% | 0,019608 | |
| Более -6% и до -5% | 0,098039 | |
| Более -5% и до -4% | 0,039216 | |
| Более -4% и до - 3% | 0,039216 | |
| Более -3% и до -2% | 0,058824 | |
| Более -2% и до -1% | 0,058824 | |
| Более - 1% и до 0% | 0,098039 | |
| Более 0% и до + 1% | 0,058824 | |
| Более + 1%идо + 2% | 0,137255 | |
| Более + 2% и до + 3% | 0,078431 | |
| Более. + 3% и до + 4%. | 0,058824 | |
| Более + 4% и до + 5% | 0,078431 | |
| Более + 5% и до + 6% | 0,019608 | |
| Более + 6% и до + 7% | 0,039216 | |
| Более + 7% и до + 8% | ||
| Более + 8% и до + 9% | ||
| Более + 9% и до + 10 | 0,039216 | |
| Более + 10% и до + 11% | ||
| Более + 11%идо+ 12% | 0,039216 | |
| Итого |
При группировке данных необходимо уделить особое внимание интервалам. Во-первых, они не должны перекрываться. Во-вторых, они должны быть одинаковых размеров, если не существует специфической потребности в выделении данных в рамках какой-либо "подгруппы", либо если данные в группе настолько малочисленны, что могут быть безопасно слиты с предыдущей или последующей группой без потери информации. В-третьих, интервалы не должны быть столь большими, чтобы скрывать характерные изменения в рамках группы. И, наконец, число интервалов должно быть компромиссом между необходимостью передачи деталей и возможностью для аналитика охватить эти детали.
1.2. Представление данных.
В этом разделе рассмотрим следующие методы представления данных:
· графики распределения значений;
· графики распределения относительных частот;
· графики распределения накопленных частот или огивы;
· гистограммы.
График распределения значений.
Для построения графика распределения значений число наблюдений откладывается по вертикальной оси, а интервалы (доходы) - по горизонтальной. Затем отмечается каждая из частот и составляется диаграмма, как на рис. 1.1. Высота каждого столбика представляет число наблюдений в рамках каждого интервала.
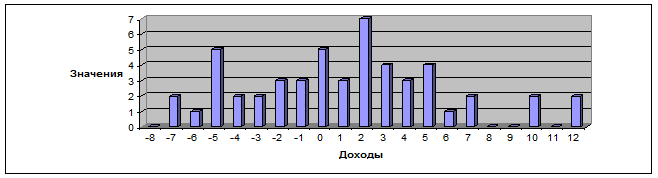
Рис. 1.1. График распределения значений.
График распределения относительных частот.
Чтобы получить относительные частоты для группы данных, необходимо число наблюдений в каждой группе разделить на общее число единиц совокупности. После этого распределение относительных частот можно изобразить графически способом, аналогичным для распределения частот. Получим диаграмму, показанную на рис. 1.2.
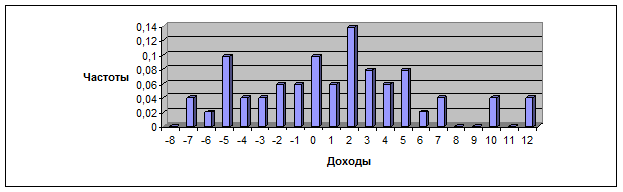
Рис. 1.2. График распределения относительных частот.
График распределения накопленных частот, или огива.
Для построения графиков распределения накопленных частот накопленное значение откладывается по вертикали, а величина интервалов – по горизонтали. Огивы строятся нанесением на ось абсцисс данных в возрастающем порядке, и в случае сгруппированных данных нанесением частот напротив верхней границы интервала. Это проиллюстрировано на рис. 1.3.
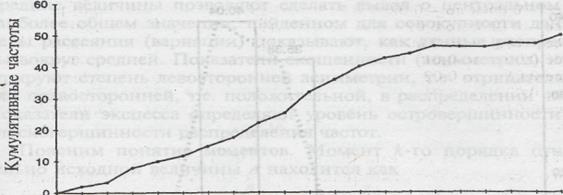
Рис. 1.3. Огива данных, представленных в таблице 1.1.
Гистограмма.
Следующим шагом в представлении относительного распределения будет его отображение не высотой, а площадью столбиков. Данное графическое представление известно как гистограмма. Гистограмма должна быть построена так, чтобы площадь каждого "столбика" представляла относительную частоту распределения, а общая их площадь составляла 100% распределения. Можно кратко изложить всю эту процедуру, сказав, что при построении гистограммы должен быть определен размер интервала. Затем рассчитывается высота каждого столбика делением относительной частоты на число единиц в конкретном интервале. Потому высота "столбиков", относящихся к интервалам, которые уже, будет больше, а относящихся к тем, которые шире, будет меньше.
1.3. Описательные статистические показатели.
Для представления обобщающих показателей, предположим, доходности активов, цен активов или числа финансовых операций, мы используем показатели центра распределения, показатели вариации, показатели скошенности (асимметрии) и показатели эксцесса.
Средние величины позволяют сделать вывод о центральном или наиболее общем значении, найденном для совокупности данных, меры рассеяния (вариации) показывают, как данные распределены вокруг средней. Показатели скошенности (асимметрии) иллюстрируют степень левосторонней асимметрии, т.е. отрицательной, или правосторонней, т.е. положительной, в распределении частот. Показатели эксцесса определяют уровень островершинности или плосковершинности распределения частот.
Поясним понятие моментов. Момент k-го порядка относительно исходной величины А находится как
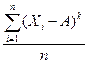
 (1.1).
(1.1).
Если А = 0 и k = 1, то мы получим среднюю арифметическую. Поэтому средняя арифметическая иногда называется моментом первого порядка относительно нуля. Если же величина А сама является средней арифметической и k=2, мы имеем момент второго порядка относительно средней (центральный момент второго порядка), известный как дисперсия, и характеризующий вариацию признака. При А, равном средней, и k = 3 получаем момент третьего порядка относительно средней (центральный момент третьего порядка), который является мерой скошенности, а если k = 4, то определяется момент четвертого порядка относительно средней (центральный момент четвертого порядка), измеряющий эксцесс.
Показатели центра распределения.
Практически каждый человек знаком с понятием средней величины, будь это "средний" размер остатка по кредитной карте, "среднее" число операций по счету и т.д. Фактически существует несколько показателей "средней", которые особенно интересны в сфере финансов. Это:
· мода;
· медиана;
· средняя арифметическая;
· средняя геометрическая.
Мода - это наиболее часто наблюдаемая величина изучаемой переменной. Для ее иллюстрации рассмотрим следующие данные, которые показывают цену акции, выраженную в рублях, в течение 15-дневного периода:
100, 120, 90, 80, 100, 150, 140, 120, 110, 100, 120, 120, 100, 120, 110.
Модой, т.е. наиболее часто повторяющимся наблюдением, является величина 120.
Медиана - это значение наблюдения, которое находится в середине ранжированного ряда данных, т.е. наблюдение, занимающее срединное положение.
Медиана для несгруппированных данных. Для определения медианы в случае несгруппированных данных мы сначала должны расположить их в возрастающем порядке. Покажем это на примере, использованном при рассмотрении моды
80, 90, 100, 100, 100, 100, 110, 110, 120, 120, 120, 120, 120, 140, 150.
Так как присутствуют 15 наблюдений, медианой является значение восьмого наблюдения, т.е. величина признака, равная 110.
Если бы в примере было четное число наблюдений, то отсутствовало бы "срединное" наблюдение, поэтому была бы рассчитана средняя из двух значений, стоящих посередине. Результатом может являться число, не присутствующее на самом деле в ряду данных.
Средняя арифметическая - наиболее часто используемый показатель центра распределения, именно ее большинство людей рассматривают в качестве средней.
Средняя арифметическая для несгруппированных данных. Средние показатели динамики - средний уровень ряда, средние абсолютные изменения и ускорения, средние темпы роста - характеризуют тенденцию. Они необходимы при обобщении характеристик тенденции за длительный период, по различным периодам; они незаменимы при сравнении развития за неодинаковые по длительности отрезки времени и при выборе аналитического выражения тренда. При наличии в динамическом ряду существенных колебании уровней определение средних показателей тенденции требует применения специальных методов статистики. В данном разделе рассматриваются только математические свойства средних показателей динамики и простейшие приемы их вычисления, применимые на практике к рядам со слабой колеблемостью.
Средняя арифметическая рассчитывается суммированием всех значений отдельных наблюдений и последующим делением полученной суммы на количество наблюдений. Например, допустим, что мы желаем подсчитать среднюю арифметическую цены какого-либо актива в течение пяти дней. В данный период мы наблюдаем следующие цены
225 225 240 215 230
Найдем среднюю арифметическую, складывая эти пять значений и деля сумму на число наблюдений. В формализованном виде средняя арифметическая выглядит так:
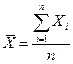 (1.2).
(1.2).
Здесь показано, что 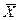 - это сумма
- это сумма 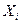 (отдельных наблюдений X), поделенная на количество наблюдений. Греческая заглавная буква сигма (
(отдельных наблюдений X), поделенная на количество наблюдений. Греческая заглавная буква сигма ( 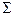 ) - оператор суммирования, означает, что все
) - оператор суммирования, означает, что все 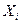 необходимо сложить вместе. Так как в нашем примере всего пять
необходимо сложить вместе. Так как в нашем примере всего пять 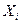 , то оператор суммирования будет выглядеть следующим образом
, то оператор суммирования будет выглядеть следующим образом 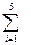 , показывая, что первые пять
, показывая, что первые пять 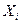 должны быть сложены друг с другом. Сейчас мы можем подсчитать среднюю арифметическую пяти цен ценной бумаги: (225 + 225 + 240 + 215 + 230)/5 = 227.
должны быть сложены друг с другом. Сейчас мы можем подсчитать среднюю арифметическую пяти цен ценной бумаги: (225 + 225 + 240 + 215 + 230)/5 = 227.
Таким образом, средняя арифметическая цена равняется 227.
В моментном ряду смысл среднего уровня заключается в том, что он характеризует уже не состояние объекта в отдельные моменты, а его среднее, обобщенное состояние между начальным и конечным моментами учета. Из этого следует, что уровни, относящиеся к начальному и конечному моментам, играют не ту роль, что уровни, относящиеся к моментам внутри изучаемого отрезка времени. Начальный и конечный уровни находятся на границе изучаемого интервала, они наполовину относятся к предыдущему и последующему интервалам и лишь наполовину к изучаемому. Уровни, относящиеся к моментам внутри осредняемого интервала, целиком относятся только к нему. Отсюда получаем особую форму средней арифметической величины, называемой хронологической средней:
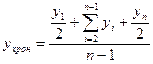 (1.3).
(1.3).
Проблема вычисления среднего уровня моментного ряда при неравных промежутках между моментами является спорной и здесь не рассматривается. Если известны точные даты изменения уровней моментного ряда, то средний уровень определяется как
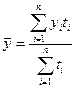 (1.4).
(1.4).
Средний абсолютный прирост(абсолютное изменение)определяется как простая арифметическая средняя из абсолютных изменений за равные промежутки времени (цепных абсолютных изменений) или как частное от деления базисного абсолютного изменения на число осредняемых отрезков времени от базисного до сравниваемого периода:
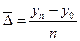 (1.5).
(1.5).
Средняя арифметическая для сгруппированных данных.Часто верхние и нижние пределы крайних интервалов остаются открытыми. Следовательно, необходимо сделать допущение о границах интервалов. Это допущение должно базироваться на характеристиках анализируемых данных. Например, данные из табл. 1.2. относятся к рыночной цене акции, которую наблюдали некоторое время аналитики. Нижний интервал обозначен "До 260 руб.", а верхний - "Более 550 руб.".
Таблица 1.2.
Интервалы цен некоторой акции.
| Интервал | Среднее значение | 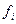
|
| До 260 руб. | 215 руб. | |
| От 260 до 400 руб. | 330 руб. | |
| От 400 до 550 руб. | 475 руб. | |
| Более 550 руб. | 585 руб. | |
| Итого |
Средняя арифметическая для сгруппированных данных находится с помощью следующей формулы
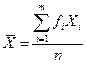 (1.6)
(1.6)
где 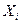 - центральное значение каждого интервала;
- центральное значение каждого интервала; 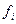 - количество наблюдений в каждом интервале; т - число интервалов; п - общее количество наблюдений или единиц совокупности.
- количество наблюдений в каждом интервале; т - число интервалов; п - общее количество наблюдений или единиц совокупности.
Используя приведенные выше данные, рассчитаем среднюю арифметическую рыночной цены акции:
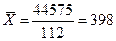 руб.
руб.
Альтернативным показателем средней арифметической, особенно хорошо подходящим для измерения средних темпов роста, является средняя геометрическая. Для иллюстрации этого сначала предположим, что фондовый индекс изменялся со следующими годовыми темпами прироста в течение пяти лет: + 10%, + 20%, + 15%, -30%, + 20%. Средняя арифметическая темпов приросту равна + 35/5 = 7. Однако 100 единиц, инвестированных в первый год, возрастут до следующих значений в каждом году соответственно: 110; 132; 151,8; 106,26; 127,51. Следовательно, фактический прирост за весь пятилетний период составляет лишь 27,5%. Разделив это число на пять, мы получим 5,5% в год; но правильный ли это ответ?
Правду говоря, нет! Что нам действительно нужно, так это единичная мера темпа прироста, которая при повторении ее n раз трансформирует начальное значение в конечное. Корректный показатель периодических темпов прироста находится с использованием средней геометрической. Для измерения среднего годового темпа прироста за n лет используется следующая формула:
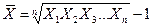 (1.7)
(1.7)
где 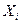 имеют вид (1 + r), авеличина r, темп прироста, выражена в десятичных дробях, т.е., например, 10% = 0,1.
имеют вид (1 + r), авеличина r, темп прироста, выражена в десятичных дробях, т.е., например, 10% = 0,1.
При использовании приведенных выше данных средняя геометрическая из темпов прироста в течение пяти лет составит 4,98%:
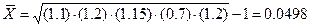
Таким образом, средняя арифметическая дает преувеличенное значение среднего годового темпа прироста в данном примере. Применение же средней геометрической дает корректную "среднюю" темпа прироста.
Какую среднюю использовать? Выбор подходящего вида средней зависит, с одной стороны, от природы данных, а с другой - от того, как этот показатель будут использовать. Средняя арифметическая особо чувствительна к экстремальным (выделяющимся) значениям в одном из направлений, которые называются смещенными данными. Выделяющиеся большие значения увеличивают среднюю выше уровня действительного представляющего точку центра распределения данных. Особо малые значения признаков имеют противоположный эффект. Иногда для того чтобы исключить влияние экстремальных единиц данных, рассчитывается усеченная средняя.Для этого просто необходимо удалить 5% наибольших и 5% наименьших наблюдений до расчета средней арифметической.
Экстремальные наблюдения не влияют на медиану и моду, но эти показатели не столь полезны в дальнейшем математическом и статистическом анализе.
Средняя геометрическая лучше других подходит, когда подсчитываются "средние" темпы прироста в течение нескольких временных периодов.
1.4. Дисперсия и среднее квадратическое отклонение.
Если средняя арифметическая выбрана как показатель центра распределения, то соответствующими показателями вариации являются дисперсия и среднее квадратическое отклонение. Дисперсия широко применяется в финансовых расчетах как мера риска и неопределенности. Среднее квадратическое отклонение используется как мера изменчивости в ценообразовании, например, опционов.
Дисперсия для несгруппированных данных. Если отдельные наблюдения сгруппированы вблизи среднего значения, то разности между каждым индивидуальным наблюдением 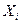 , и средней
, и средней 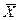 будут небольшими. Если отдельные наблюдения широко рассеяны, то разности между каждым индивидуальным значением
будут небольшими. Если отдельные наблюдения широко рассеяны, то разности между каждым индивидуальным значением 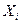 , и средней
, и средней 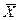 будут велики.
будут велики.
Можно предположить, что с помощью суммирования всех ( 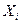 -
- 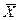 ) мы получим меру рассеяния. К сожалению, это не так, потому что
) мы получим меру рассеяния. К сожалению, это не так, потому что 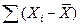 всегда равна нулю. Для преодоления этого свойства средней необходимо возвести в квадрат каждое отклонение (
всегда равна нулю. Для преодоления этого свойства средней необходимо возвести в квадрат каждое отклонение ( 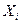 -
- 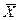 ) и просуммировать получившиеся значения. Деление результата на n-1, т.е. на количество наблюдений минус один, дает дисперсию. Это можно записать в формализованном виде:
) и просуммировать получившиеся значения. Деление результата на n-1, т.е. на количество наблюдений минус один, дает дисперсию. Это можно записать в формализованном виде:
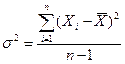 (1.8).
(1.8).
Если вычисляется дисперсия на основе всей совокупности данных, то делитель в выражении (1.8) равен n. Однако когда данные, которыми мы располагаем, представляют выборку из всей совокупности данных, что обычно случается в эмпирических исследованиях в области финансов, следует делить на n-1. Происходит это потому, что мы должны делить на то, что статистики называют степенями свободы, для предотвращения искажения результата. Степени свободы - это число наблюдений минус число параметров, оцененных по рассматриваемым данным. В случае дисперсии средняя оценивается по тем же данным. Таким образом, когда эта оценка используется при вычислении среднего квадратического отклонения, число степеней свободы равно n-1. Наибольший эффект при коррекции n на число степеней свободы наблюдается для малых выборок. Понятно, что для большого объема данных эффект коррекции минимален.
Пример. Найдите самостоятельно дисперсию переменной Х, значения которой приведены в таблице 1.3.
Таблица 1.3.
| Значения переменной Х | 2407,5 | 2289,2 | 2160,1 | 2311,1 | 2425,8 | 2378,4 | 2245,5 | 2229,2 | 2118,8 | 2372,4 | 2376,3 |
Ответ: 10520.15.
Дисперсия для сгруппированных данных. При использовании сгруппированных данных формула дисперсии выглядит так:
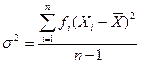 (1.9),
(1.9),
где 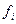 - количество наблюдений в каждом интервале,
- количество наблюдений в каждом интервале, 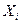 - центральное значение каждого интервала, а
- центральное значение каждого интервала, а 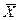 - среднее значение всех Х.
- среднее значение всех Х.
Пример. Вычислить дисперсию сгруппированных данных, представленных в таблице 1.2.
Среднее квадратическое отклонение. Дисперсия выражается в квадратах единиц, находящихся в основании расчета, что делает ее интерпретацию довольно затруднительной. Эту проблему можно преодолеть, извлекая квадратный корень из дисперсии и получая, таким образом, среднее квадратическое отклонение, обозначаемое как 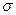 .
.
Среднее квадратическое отклонение для несгруппированных данных. Среднее квадратическое отклонение вычисляется так:
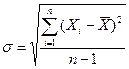 (1.10).
(1.10).
Среднее квадратическое отклонение для сгруппированных данных. Формула для нахождения среднего квадратического отклонения для сгруппированных данных выглядит так;
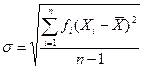 (1.11).
(1.11).
Это опять только квадратный корень из дисперсии, но на этот раз для сгруппированных данных.
Коэффициент вариации. Среднее квадратическое отклонение выражается в единицах измерения, лежащих в основе расчета. Таким образом, при сравнении степени вариации переменных должны быть учтены различия в величине этих переменных. Для этого нужно рассчитать коэффициент вариации. Он находится как отношение:
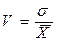 (1.12).
(1.12).
Коэффициент асимметрии. Иногда бывает важно знать, есть ли смещения в рассеянии данных. Индикатор этих смещений - скошенность (асимметрия) данных. В случае положительной асимметрии распределение имеет длинную правую ветвь. Средняя величина дохода больше медианы, которая в свою очередь больше моды. Значение средней больше медианы и моды, потому что на нее повлияли несколько очень больших значений доходов.
Отрицательная асимметрия проявляется в виде более длинной левой ветви, а величина средней меньше медианы и моды. Большинство наблюдений распределения имеют значения больше средней, но величина средней снижается из-за нескольких очень малых наблюдений.
При симметричном распределении средняя, медиана и мода имеют одно и то же значение.
Показателем асимметрии, который наиболее пригоден для применения в случае сгруппированных данных, является коэффициент асимметрии, основанный на расчете моментов распределения. Он определяется с помощью центрального момента третьего порядка и деления его на куб среднего квадратического отклонения, что можно представить следующей формулой:
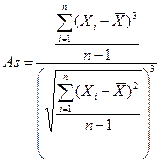 (1.13).
(1.13).
Эксцесс. В то время как показатели асимметрии характеризуют симметричность распределения частот, показатели эксцесса описывают пиковость этого распределения. Распределения, имеющие более выраженный пик, чем у нормального распределения (о нем детально рассказано далее), называются островершинными. Те же распределения, у которых степень вытянутости вдоль оси ординат меньше, чем у нормальной кривой, называются плосковершинными, а распределения, которые похожи на нормальное, - средневершинными. Островершинные распределения можно увидеть в доходах активов, когда наблюдаются периодические скачки в ценах на эти активы. Рынки с прерывающимся процессом торговли, как, например, рынки ценных бумаг, которые закрываются на ночь и в выходные, имеют большую вероятность для демонстрации скачков цен активов. Причиной служит то, что информация, которая влияет на цены, но публикуется во время закрытия рынков, окажет воздействие на цены, когда рынок откроется вновь, таким образом создавая условия для скачка между предыдущей ценой закрытия и ценой открытия. Этот скачок цен, наиболее заметный для ежедневных или еженедельных данных, приведет к более высокой частоте повторения больших положительных или отрицательных доходов, чем предполагалось бы, если бы торговля на рынках велась непрерывно. Коэффициенты эксцесса могут быть определены с помощью центральных моментов распределения. Коэффициент эксцесса находится делением центрального момента четвертого порядка на среднее квадратическое отклонение, возведенное в четвертую степень:
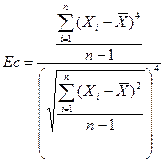 (1.14).
(1.14).
Если данные будут нормально распределены, то коэффициент эксцесса, рассчитанный с помощью формулы (1.11), равнялся бы 3.
1.5. Показатели статистической связи.
Выше объяснялось, что дисперсия случайной переменной показывает, как наблюдаемые значения этой переменной распределены вокруг среднего значения. Здесь введем понятие ковариации, которая показывает, как две случайные переменные ведут себя по отношению одна к другой. Затем мы перейдем к расчету коэффициента корреляции, который является наиболее удобным показателем степени линейной связи между двумя переменными.
Ковариация. В финансовой и других областях встречается много ситуаций, когда важно знать, как две переменные ведут себя по отношению друг к другу. Например, в управлении портфелем ценных бумаг для определения риска портфеля активов необходимо знать, как цена ценной бумаги Х ведет себя по отношению к ценной бумаге Y для всех пар активов. Другими словами, нам нужно определить ковариацию или корреляцию каждой пары активов.
Если цена ценной бумаги X обычно растет (падает) в то же время, когда растет (падает) цена ценной бумаги Y, ковариация будет положительной. Однако если обычно во время роста цены ценной бумаги X цена ценной бумаги Y падает, то ковариация будет отрицательной. Если же не существует определенной модели связи между движениями цен, т.е. цены двух ценных бумаг ведут себя независимо, ковариация равна нулю. Формула для вычисления ковариации выглядит следующим образом:
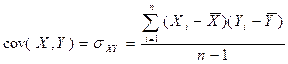 (1.15).
(1.15).
Как видно из формулы, величина ковариации зависит от величины наблюдений Х и Y. Таким образом, значительная ковариация может быть вызвана в большей степени высокими значениями наблюдений, чем близкой связью между переменными.
Дисперсионно-ковариационная матрица. Часто ковариации нескольких переменных (например X, Y, Z) изображаются в виде дисперсионно-ковариационной матрицы С:
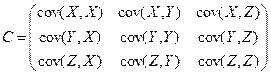 (1.16).
(1.16).
Возможными парами активов в этом примере являются XX, ХY, ХZ, YХ, YY, YZ, ZХ, ZУ и ZZ. Таким образом, ковариация X и Y - это то же самое, что и ковариация Y и X. Поэтому все ковариации левее и ниже диагонали повторяются выше и правее диагонали. Значит, эти ковариации введены в матрицу дважды. Важность этой детали проиллюстрируем позднее, когда будем измерять риск портфеля. Ковариации на диагонали - это ковариации доходов с ними самими. Ковариация переменной с ней самой равняется дисперсии этой переменной. Для понимания этого используем выражение (1.10) для измерения ковариации актива X с ним самим. Равенство будет выглядеть так:
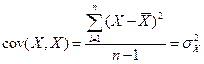 (1.17),
(1.17),
что совпадает с формулой дисперсии.
Коэффициент корреляции. Наиболее широко используемым показателем степени связи между двумя переменными является коэффициент корреляции. Это показатель, независимый от единиц измерения, характеризует силу и направление линейной связи между двумя переменными. Следовательно, при его использовании преодолевается недостаток ковариации, так как величина коэффициента корреляции не находится под влиянием значений наблюдений.
Значения коэффициента корреляции находятся в промежутке от (- 1) для случая отрицательной связи, проходя через 0, где две переменные независимы друг от друга и заканчиваются в точке (+ 1) для случая положительной связи между переменными.
Коэффициент корреляции 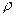 рассчитывается делением коэффициента ковариации между X и Y на произведение среднего квадратического отклонения X и среднего квадратического отклонения Y. В формализованном виде это записывается так:
рассчитывается делением коэффициента ковариации между X и Y на произведение среднего квадратического отклонения X и среднего квадратического отклонения Y. В формализованном виде это записывается так:
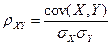 (1.18).
(1.18).
Независимо от того, положительна или отрицательна корреляция, коэффициент корреляции - это только мера статистической связи. В статистике выводы о причинности, т.е. возможности предположить, что изменение переменной X приведет к изменению переменной Y или наоборот, нельзя сделать, использовав коэффициент корреляции: для этого существует, например, тест Гранжера. Следовательно, коэффициент корреляции может лишь показать, насколько сильна линейная связь между двумя переменными, но не может объяснить их изменений.
1.6. Показатели, характеризующие тенденцию динамики.
Для того чтобы построить систему показателей, характеризующих тенденцию динамики, нужно подобрать величины, которые характеризуют изменения уровней анализируемого ряда как в абсолютном, так и в относительном выражении. Далее финансового аналитика, как правило, интересует, является ли изменение временного ряда равномерным или неравномерным, ускоренным или замедленным. Наконец, его интересует уравнение тенденции ряда в форме некоторого достаточно простого выражения, наилучшим образом аппроксимирующего фактическую тенденцию динамики. Понятие об уравнении тенденции динамики было введено в статистику английским ученым Гукером в 1902 г. Он предложил называть такое уравнение трендом (trend).
Для того чтобы нагляднее представить показатели, характеризующие тенденцию, следует абстрагироваться от колеблемости и выявить динамический ряд в форме «чистого» тренда при отсутствии колебаний. Пример такого ряда представлен в табл. 1.4.
Абсолютное изменение уровней - в данном случае его можно назвать абсолютным приростом - это разность между сравниваемым уровнем и уровнем более раннего периода, принятым за базу сравнения. Если эта база - непосредственно предыдущий уровень, показатель называют цепным, если за базу взят, например, начальный уровень, показатель называют базисным. Формулы абсолютного изменения уровня:
цепное : 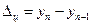
базисное : 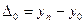 (1.19).
(1.19).
Если абсолютное изменение отрицательно, его следует называть абсолютным сокращением. Абсолютное изменение имеет ту же единицу измерения, что и уровни ряда с добавлением единицы времени, за которую определено изменение: 22 тыс. руб. в год (или в месяц, или в пятилетие). Без указания единицы времени, за которую произошло измерение, абсолютный прирост нельзя правильно интерпретировать.
Таблица 1.4.
Абсолютные и относительные показатели тенденции.
| Номер периода | Уровень ряда (тыс. руб.) | Абсолютное изменение уровней (тыс. руб. в год) | Ускорение абсолютного изменения (тыс. руб. в год) | Темп роста уровня к периоду, % | |
| предыдущему | Начальному | ||||
| 0 (начальный) | - | - | - | - | |
| - | |||||
| 114,3 | |||||
| 115,6 | |||||
| 116,2 | |||||
| 116,3 | |||||
| 116.0 |
В табл. 1.4 абсолютное изменение уровня не является константой тенденции. Оно со временем возрастает, т.е. уровни ряда изменяются с ускорением. Ускорение - это разность между абсолютным изменением за данный период и абсолютным изменением за предыдущий период равной длительности:
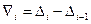 (1.20).
(1.20).
Показатель абсолютного ускорения применяется только в цепном варианте, но не в базисном. Отрицательная величина ускорения говорит о замедлении роста или об ускорении снижения уровней ряда.
Как видно из табл. 1.4, ускорение является константой тенденции данного ряда, что свидетельствует о параболической форме этой тенденции. Ее уравнение имеет вид:
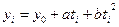 (1.21),
(1.21),
где где у0 - уровень ряда в начальный (нулевой) период; а - средний абсолютный прирост (по всему ряду); b - половина ускорения; 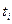 - номера периодов.
- номера периодов.
По данным табл. 1.4 имеем:
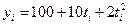
Показатель ускорения абсолютного изменения уровней выражается в единицах измерения уровня, деленных на квадрат длины периода. В нашем случае ускорение составило 4 тыс. руб. в год за год. Смысл показателя следующий: стоимость объема продаваемых акций имел абсолютный прирост, возрастающий на 4 тыс. руб. в год ежегодно.
Усвоить рассмотренные показатели поможет следующая аналогия с механическим движением: уровень - это аналог пройденного пути, причем начало его отсчета не в нулевой точке; абсолютный прирост - аналог скорости движения тела, а ускорение абсолютного прироста - аналог ускорения движения. Пройденный телом путь, считая и тот, который уже был пройден до начала отсчета времени в данной задаче, равен:
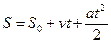 (1.22),
(1.22),
где 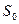 - путь, пройденный до начала отсчета времени; v – скорость движения; а - ускорение; t - время, прошедшее от начала его отсчета в задаче.
- путь, пройденный до начала отсчета времени; v – скорость движения; а - ускорение; t - время, прошедшее от начала его отсчета в задаче.
Система показателей должна содержать не только абсолютные, но и относительные статистические показатели. Относительные показатели динамики необходимы для сравнения развития разных объектов, особенно если их абсолютные характеристики различны. Предположим, что тенденция объема продаж другого вида ценных бумаг характеризуется следующим уравнением: 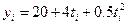 . И абсолютный прирост, и ускорение роста объема продаж во втором случае гораздо меньше, чем в первом. Но можно ли ограничиться этими показателями и сделать вывод, что развитие продаж второго вида ценных бумаг происходит более медленными темпами, чем первого? Меньший уровень еще не есть меньший темп развития, и это покажет относительная характеристика тенденции динамики - темп роста.
. И абсолютный прирост, и ускорение роста объема продаж во втором случае гораздо меньше, чем в первом. Но можно ли ограничиться этими показателями и сделать вывод, что развитие продаж второго вида ценных бумаг происходит более медленными темпами, чем первого? Меньший уровень еще не есть меньший темп развития, и это покажет относительная характеристика тенденции динамики - темп роста.
Темп роста - это отношение сравниваемого уровня (более позднего) к уровню, принятому за базу сравнения (более раннему).Темп роста исчисляется в цепном варианте - к уровню предыдущего года, а в базисном - к одному и тому же, обычно начальному уровню. Он свидетельствует о том, сколько процентов составляет сравниваемый уровень по отношению к уровню, принятому за базу, или во сколько раз сравниваемый уровень больше у ровня, принятого за базу. При этом если уровни снижаются со временем, то сказать, что последующий уровень «больше в 0,75 раза», или составляет 75% базового уровня, это, разумеется, означает, что уровень уменьшился на четверть. Темп изменения в разах всегда говорит о том, во сколько раз сравниваемый уровень больше предыдущего.
Рассмотрим связь абсолютныхи относительных показателен динамики. Обозначим темп изменения через k, тогда имеем:
цепной темп роста в период с номером n: 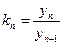
базисный темп роста за весь период: 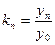
Если сравниваемый уровень выразить через уровень базисного (или предыдущего) периода и абсолютное изменение, получим:
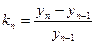 (1.23).
(1.23).
Величина k в уравнении (1.23), т.е. отношение абсолютного изменения к уровню предыдущего (или базисного) года, называется относительным приростом(относительным сокращением, относительным изменением, процентным изменением) или темпом прироста.
Темп изменения - величина всегда положительная. Если уровень ряда динамики принимает положительные и отрицательные значения, например, финансовый результат от реализации продукции предприятием может быть прибылью (+), а может быть убытком (-), тогда темп изменения и темп прироста применять нельзя. В этом случае такие показатели теряют смысл и не имеют экономической интерпретации. Сохраняют смысл только абсолютные показатели динамики.
Рассмотрим соотношения между цепными и базисными показателями на примере данных табл. 1.4:
1) сумма цепных абсолютных изменений равна базисному абсолютному изменению: 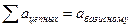
12+16+20+24+28+32=232-100=132
2) произведение цепных темпов изменения равно базисному темпу изменения: 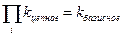
1,12 * 1,143 * 1,156 * 1,162 * 1,163 * 1,16 = 2,32.
Значения цепных темпов прироста, рассчитанных каждый к своей базе, различаются не только числом процентов, но и величиной абсолютного изменения, составляющей каждый процент. Следовательно, складывать или вычитать цепные темпы прироста нельзя. Абсолютное значение 1%-ного прироста равносотой части предыдущего уровня или базисного уровня.
Средний темп изменения определяется наиболее точно при аналитическом выравнивании динамического ряда по экспоненте. Если можно пренебречь колеблемостью, то средний темп определяют как геометрическую среднюю из цепных темпов роста за п лет или из общего (базисного) темпа роста за nлет:
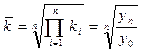 (1.24).
(1.24).
Например, стоимость потребительской корзины за год в результате инфляции возросла в три раза. Каков средний месячный темп инфляции?
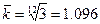 , или 1.096%,
, или 1.096%,
т.е. в среднем за месяц цена увеличивалась на 9.6% к уровню предыдущего месяца.
Средний темп роста так же, как средний прирост, следует сопровождать указанием двух единиц времени: периода, который им характеризуется, и периода, на который рассчитан, например, среднегодовой темп за последнее десятилетие; среднемесячный темп за полугодие и т.д.
Если исходной информацией служат темпы прироста и нужно вычислить их среднегодовую величину, то предварительно следует все темпы прироста превратить в темпы роста, прибавив 1, или 100%, вычислить их среднюю геометрическую и снова вычесть 1, или 100%. Интересно, что ввиду асимметрии темпа прироста и темпа сокращения при равных их величинах общий темп прироста всегда отрицателей. Так, если за первый год объем производства вырос па 20%, а за второй снизился на 20% (темпы цепные), то за два года имеем:
- средний темп роста 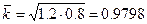 или 97,98%;
или 97,98%;
- средний темп прироста 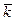 - 1 = -0,0202, или -2,02%.
- 1 = -0,0202, или -2,02%.
Интересную задачу представляет определение срока, за который ряд с большим средним показателем динамики, но меньшим начальным уровнем догонит другой ряд с большим начальным уровнем, по меньшим показателем динамики. Для абсолютных приростов задача элементарна: имеем одни ряд с базисным уровнем 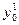 и средним абсолютным приростом
и средним абсолютным приростом 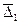 ; второй ряд с показателями соответственно
; второй ряд с показателями соответственно 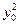 ,
, 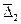 , причем
, причем 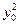 >
> 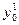 ,
, 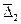 <
< 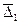 . Уровень первого ряда сравняется с уровнем второго ряда через n лет:
. Уровень первого ряда сравняется с уровнем второго ряда через n лет:
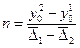 (1.25).
(1.25).
| <== предыдущая лекция | | | следующая лекция ==> |
| АТФ и ГТФ как источники энергии | | | Методы корреляционно-регрессионного анализа фондового рынка. 1 страница |
Дата добавления: 2017-10-09; просмотров: 1894;
