Точность вычислений

Приближенные вычисления

На практике в большинстве случаев найти точное решение возникшей математической задачи не удается. Это происходит потому, что искомое решение обычно не выражается в элементарных или других известных функциях. Поэтому большое значение приобрели численные методы. Под численными методами подразумеваются методы решения задач, сводящиеся к действиям над числами, то есть к тем действиям, которые выполняет компьютер.

Решение, полученное численным методом, обычно является приближенным, то есть содержит некоторую погрешность. Это происходит потому, что численным методом обычно решается другая, более простая задача, приближающая исходную задачу. В ряде случаев численный метод строится на базе бесконечного процесса, который, прерванный на некотором шаге, дает приближенное решение.

Большинство численных методов основано на замене сложных объектов более простыми. Одно из главных понятий в математике – функция. Наиболее удобной для расчетов функцией является многочлен. Его значения просто вычисляются, поэтому алгебраические многочлены широко применяются для приближения функций.

Ряд Тейлора

Большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания.

Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций. Ряды Тейлора применяются для аппроксимации функции многочленами.Аппроксимация (приближение) – это научный метод, состоящий в замене одних формул другими, более простыми для расчета.

Запись бесконечного ряда Тейлора:

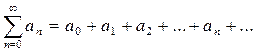
a_n называется общим членом ряда.

Сумму бесконечного ряда невозможно считать так же, как конечную сумму. Поэтому следует ввести несколько определений.

Частичной суммой ряда называется выражение вида

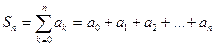
Можно составить бесконечную последовательность частичных сумм S₀, S₁,… S_n,…:

S₀ = a₀

S₁ = S₀ + a₁

S₂ = S₁ + a₂ и так далее

Сходящимся называется ряд 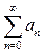, у которого последовательность частичных сумм имеет предел – число 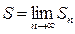. Это число называется суммой сходящегося ряда. Если же последовательность частичных сумм стремится к бесконечности, ряд называется расходящимся.

Множество значений аргумента, при которых ряд сходится, называется областью сходимости этого ряда.

Необходимый признак сходимости ряда. Если ряд 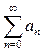сходится, то предел общего члена ряда при бесконечном увеличении номера n равен нулю: .

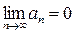Иллюстрацией к сказанному служат графики, построенные с помощью пакета AGrapher:

График зависимости членов ряда и частичных сумм от номера члена ряда для разложения функции sin(4.0)

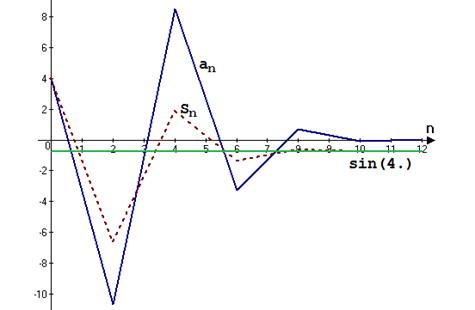
График зависимости членов ряда и частичных сумм от номера члена ряда для разложения функции CosH(3.0) (гиперболический косинус)

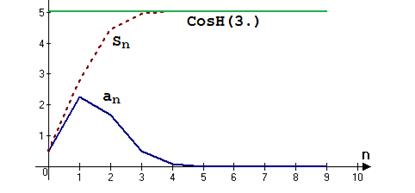
Точность вычислений

Чтобы получить приближенное значение функции, вычисляя сумму ряда, следует ограничить количество слагаемых. При замене бесконечной суммы частичной суммой ряда вносится методическая погрешность, которая количественно оценивается по первым отброшенным членам ряда.

Выбирая критерий (условие) прекращения суммирования ряда, воспользуемся необходимым признаком сходимости ряда 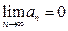. Это означает, что для любого положительного ε существует номер n, начиная с которого для всех членов ряда |a_n| < ε. Выбрав значение ε достаточно малым, можно прекратить суммирование ряда при условии
|a_n | < ε.

Значение ε будем называть заданной погрешностью вычислений. Точность вычислений тем выше, чем меньше погрешность. Очевидно, что заданная погрешность не может быть равна 0.

Выбирая точность вычислений, надо исходить из целей решаемой задачи. Например, для изображения графика на экране компьютера вполне достаточно погрешности
ε =10^-2.

Для переменных типа realдостижима минимальная погрешность ε =10^-6 ÷ 10^-7; используя переменные типа double precision, можно выбрать погрешность
ε =10^-15 ÷ 10^-16.

Если задать слишком высокую степень точности, не согласовав ее с типами используемых переменных, например, ε =10^-15 для переменных типаreal, программа может зациклиться, так как неравенство | a_n | < ε никогда не выполнится.

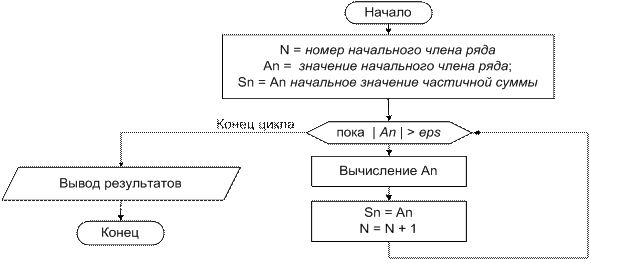
Общая идея решения поставленной задачи иллюстрируется блок-схемой.

1) Переменная An используется в программе для вычисления текущего члена ряда из последовательности a₀ , a₁ , … a_n , по очереди принимая перечисленные значения. Аналогично переменная Sn по очереди принимает значения частичных сумм. После выхода из цикла переменная Sn равна сумме ряда.

2) Суммирование членов ряда выполняется в цикле
do while«пока |An| > eps», выход из цикла при условии |a_n | < ε.

Кроме методической погрешности на общую погрешность вычислений, влияет постоянно накапливающаяся погрешность округления. Погрешность округления – это инструментальная погрешность, связанная с ошибками процессора при работе с вещественными числами. Уменьшение погрешности округления достигается применением рекуррентных формул.