Термодинамическое обоснование законов Коновалова.
Для идеальных жидких растворов из двух компонентов (А и В), па которых также можно считать идеальным газом, согласно закону Рауля можно записать
p 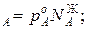 p
p 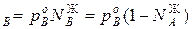
где р 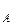 ,р
,р 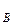 ,р
,р 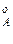 ,р
,р 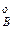 – парциальное давление компонентов А и В раствора и чистых веществ соответственно; N
– парциальное давление компонентов А и В раствора и чистых веществ соответственно; N 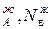 – мольные доли компонентов А и В соответственно в жидком растворе.
– мольные доли компонентов А и В соответственно в жидком растворе.
Поделим эти два уравнения друг на друга и получим:
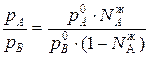 (1)
(1)
Из уравнения состояния можно определить мольную долю компонента А в паровой фазе:
рАV=NАпRT
pBV=NBпRT=(1-NAп)RT , т.е.
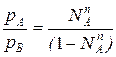 (2)
(2)
где N 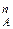 – мольная доля компонента А в паровой фазе.
– мольная доля компонента А в паровой фазе.
Приравнивая уравнения 1 и 2,получим
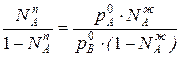
Отношения между мольными долями компонентов в паровой и жидкой фазах можно выразить следующим образом:
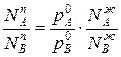 (3)
(3)
Уравнение 3 показывает изменение состава жидкости и пара в соответствии с законами Коновалова. Действительно если рA0> рВ0 (см.диагр.2), то NAп / NВп >N 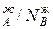 , N
, N 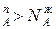 и подтверждается условие N
и подтверждается условие N 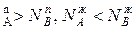 ,характеризующее первый закон Коновалова. Если рA0= рВ0, то правая и левая части уравнения
,характеризующее первый закон Коновалова. Если рA0= рВ0, то правая и левая части уравнения
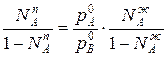
равны и становится справедливым равенство NAп = NAж ; NВn= NВж. Условие равенства парциальных давлений компонентов А и В соответствует азеотропной точке О, что фиксируется вторым законом Коновалова.
Дата добавления: 2017-09-19; просмотров: 734;
