Генотипическая гетерогенность популяций

Популяция – это единая система обмена генетической информацией между составляющими ее особями. Вследствие этого она обладает адаптивными механизмами, при помощи которых поддерживается ее существование. Как уже отмечалось, даже "вредная мутация", попав в генетический фонд популяции, остается в ней в скрытом для естественного отбора виде. С. С. Четвериков [1926] отмечал, что вид, как губка, впитывает гетероэиготные геновариации, оставаясь при этом внешне (фенотипически) однородным. За внешним однообразием популяции скрыто огромное разнообразиеее генетического материала. Благодаря этому популяция приобретает высокую пластичность для при­способления к постоянно меняющимся условиям существования. Популяция как система позволяет виду сохранять и использовать не только наследственные изменения, появившиеся в течение жизни одного поколения, но и возможные в целом ряде поколений. Эта насыщенность популяции всевозможными му­тациями не нарушаетее целостности, сохраняет эту систему в устойчивом равновесии. Как же осуществляется этот процесс сохранения колоссального запаса генетического разнообразия и одновременно целостности и устойчивости к всевозможным вариациям внешней среды.

В 1908 г. была предложена схема-формула распределения геноти­пов в популяции, вошедшая в науку под названием закона Харди – Вайнберга. Закон кажется интуитивным и слишком простым, чтобы нуждаться в объяснений. Теорема, используемая для доказательства этого, интересна тем, что дает простой пример применения математики и селекции. Этот закон гласит: в популяции, в которой осуществляется панмиксия. Отсутствует мутационный процесс,

Отсутствует давление отбора и которая бесконечно велика, сохраняется неизменным равновесие между частотами генотипов,

определяемых диаллельным геном А и а, которое выражается сле-следующим образом: p² (АА)+2 pq (Аа) + q²(aa)= (р + q)² =1, где р, q -частота генотипов в популяции. Эта формула показывает численное соотношение генотипов в популяции для одного моногенного признака. И это соотношение сохраняется в популяции из поколения в поколение. Кроме того, из формулы следует, что гетерозиготные генотипы более выгодны для популяции: ведь даже самый редкий аллель будет распространен в популяции в форме гетерозиготы; для малых значений q (если q частота редкого аллеля) q 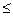2pq. Эту особенность популяции отметил еще в 1926 г. С. С. Четвериков [1929]: «Видовое сообщество (т, е, популяция) в условиях свободного скрещивания представляет собой устойчивый агрегат, внутри которого в самих условиях свободного скрещивания заложен аппарат стабилизации численных отношений, составляющих его аллеломорфных пар». Для процессов, создающих устойчивость популяции к воздействиям внешней среды, М. Лернером [Lerner, 91] был предложен термин — генетический гомеостаз. Он определил его как процесс, обеспечивающий способность популяции сохранять свою генетическую структуру в ответ на воздействие факторов внешней среды.

Пример. Родительское поколение образует гаметы А и а в отношении р : q. Последние вF₁ образуют деревьяАА, Аа и аа, частота встречаемости которых соответствует биномиальному распределениюр² : 2pq : q². ДеревьяF₁образуют гаметы следующим образом: деревьяАА дают р² гаметА; деревьяАа - pq гамет А и pq гамет а; деревьяаа -q² гамет а. Все деревья вместе дают(р² + pq) гаметА и(pq + q²) гамет а. Таким образом, отношение гамет А к гаметам а в поколенииF₁ равно(р² + pq); (q² + pq) = p(p+q): q(p + q) = р :q, как в исходной генерации.