Математическое моделирование паритета потребностей

Обеспечение оптимальной (с точки зрения паритета потребности организма в различных нутриентах) структуры ингредиентного состава пищевых продуктов достигалось с учётом их экономической доступности для потребителей и их специфических потребностей в них. Это и составило сущность математического моделирования путём достижения паритетавыше обозначенной потребности.

Метод математического моделирования предполагает оптимизацию суммарных критериев оценки этих потребностей, как в абсолютных, так и в относительных значениях. При этом оптимизируется баланс потребностей (продуктового состава рациона питания или отдельного блюда как самостоятельного функционального продукта питания) при заданных конечных требованиях такого баланса.

Конечный баланс потребностей можно представить вектором в соответствии с формулой (5.1)

d = (d₁, d₂, ..., d_k), (5.1)

где d_i – параметры оптимизации.

При этом суммарная потребность (m) рассчитывается по формуле (5.2), а интегральная оценка (Q) по формуле (5.3)

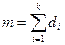, (5.2)

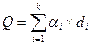, (5.3)

где α_l – коэффициент значимости отдельного ингредиента или нутриента.

Для компонент вектора, соответственно, получатся следующие значения по формуле (5.4)

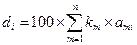, (5.4)

где i=1,2,…,k;

k_m- количество товаров с номером m (в долях от 100 %).

Вариационные ограничения каждого ингредиента описываются формулой (5.5). Условия подбора эталонного вектора (d^*) отражены в формуле (5.6 и 5.7). Кроме того, существуют ограничения, представленные формулой (5.8)

α_m ≤ k_m ≤ b_m ; (5.5)

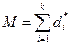; (5.6)

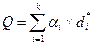; (5.7)

. (5.8)

Математическая модель баланса потребностей показана в формулах (5.9 – 5.15)

a_m = (a_m1, a_m2,…, a_mk), (5.9)

где m=1,2,…,n, удовлетворяющая условиям:

a_mi≥0 , (5.10)

. (5.11)

Целевой вектор задается по формуле (5.12)

d^*=(d^*₁,d^*₂,…,d^*_k) (5.12)

и, линейная комбинация векторов a₁, a₂,…,a_n с коэффициентами k₁, k₂,…,k_n. В этих условиях

d= k₁×a₁+k₂×a₂+…+k_n×a_n , (5.13)

где d- также вектор размерности n.

По условиям оптимизации баланса потребностей находится такие значения k_i при заданных ограничениях

α_i ≤ k_i ≤ β_i , (5.14)

где i=1,2,….,n, чтобы норма отклонения 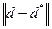была минимальной.

В качестве нормы использована обобщенная евклидова норма по формуле (5.15)

. (5.15)