Момент инерции диска (цилиндра) относительно оси симметрии (проходящей через точку 0 перпендикулярно плоскости рисунка).

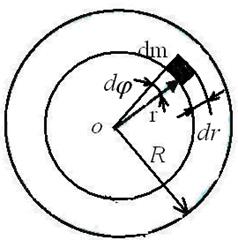
Рис. 7.2. Момент инерции однородного диска. Элемент массы

Пусть масса однородного диска т, а его радиус и толщина равны R и h, соответственно. Тогда момент инерции маленького кусочка dm равен:

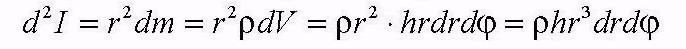
где р - плотность диска, r -расстояние до оси вращения, а элемент объема dV взят в цилиндрической системе координат. Интегрируя по углам j и радиусу r, получаем момент инерции диска (цилиндра):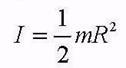

Второй способ

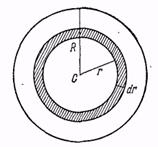
Рис. 7.3. Момент инерции однородного диска. Разбиение на кольца

Рассмотрим бесконечно тонкое кольцо с внутренним радиусом r наружным радиусом

r + dr. Площадь такого кольца 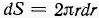Его момент инерции равен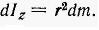

Момент инерции всего диска определяется интегралом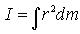

Или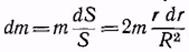

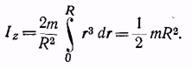
Момент инерции однородного шара массы т и радиуса R относительно оси проходящей через центр.

Первый способ

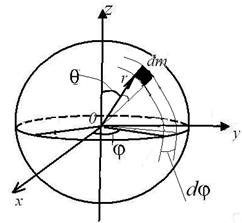
Рис. 7.4 Момент инерции однородного шара относительно оси, проходящей через его центр

Удобнее рассматривать в сферической системе координат, тогда момент инерции элемента dm равен:

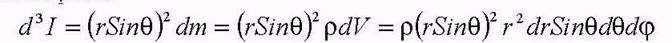
где 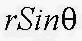расстояние кусочка массы dm до оси вращения, r - плотность шара. Интегрируя по всем переменным:

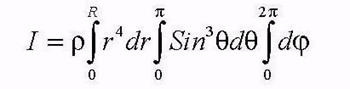
и учитывая, что масса шара равна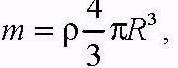

получаем момент инерции шара относительно оси симметрии:

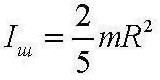
2 способ

Сплошной шар можно рассматривать как совокупность бесконечно тонких сферических слоев с массами dm . Так как шар по предположению однороден, то ,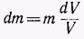

где 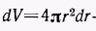—объем сферического слоя, 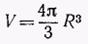— объем всего шара.

Момент инерции сферического слоя относительно диаметра равен

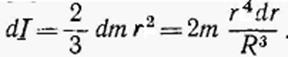
Интегрируя, получаем момент инерции сплошного шара

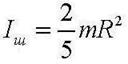
Вычисление момента инерции тела относительно оси часто можно упростить, вычислив предварительно момент инерции его относительно точки. Сам по себе момент инерции тела относительно точки не играет никакой роли в динамике. Он является чисто вспомогательным понятием, служащим для упрощения вычислений. Моментом инерции тела относительно точки О называется сумма произведений масс материальных точек, из которых тело состоит, на квадраты их расстояний R до точки О.

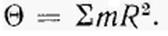
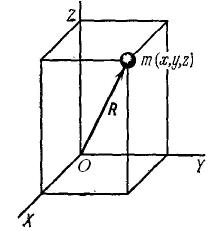
Рис. 7.5. Момент инерции относительно точки

В случае непрерывного распределения масс эта сумма сводится к интегралу 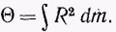Само собой понятно, что момент в не следует смешивать с моментом инерции I относительно оси. В случае момента I массы dm умножаются на квадраты расстояний до этой оси, а в случае момента Q — до неподвижной точки.

Рассмотрим сначала одну материальную точку с массой т и с координатами х, у, z относительно прямоугольной системы координат (рис. 7.5). Квадраты расстояний ее до координатных осей X, Y, Z равны соответственно , ^;,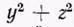

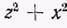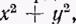
а моменты инерции относительно тех же осей

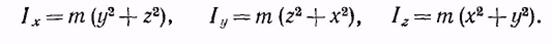
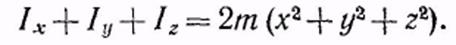
Hi 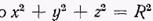, где R — расстояние точки т от начала координат О. Поэтому

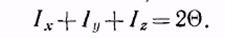
Это соотношение справедливо не только для одной материальной точки, но и для произвольного тела, так как тело можно рассматривать как совокупность материальных точек. Таким образом, сумма моментов инерции тела относительно трех взаимно перпендикулярных осей, пересекающихся в одной точке О, равна удвоенному моменту инерции того же тела относительно этой точки.

Если повернуть координатные оси X, Y, Z относительно тела, оставляя углы между ними прямыми, то моменты инерции I_x, I_y, I_z, вообще говоря, изменятся. Однако их сумма останется той же самой, так как она равна 2Q, а величина Q не зависит от ориентации координатных осей. Таким образом, сумма моментов инерции I_x, I_y, I_z, относительно любых, трех взаимно перпендикулярных осей, проходящих через одну точку, зависит только от положения этой точки и не меняется с изменением ориентации осей. Более глубокая геометрическая природа этого утверждения раскрывается в тензорной алгебре.