Второе начало термодинамики
Различают удельную и молярную теплоемкость
удельная теплоемкость:
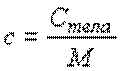
| (11.5) |
молярная теплоемкость:
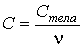 , ,
| (11.6) |
где: 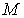 - масса тела,
- масса тела, 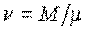 - количество вещества в нем.
- количество вещества в нем.
Эти теплоемкости связаны между собой через молярную массу М 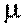 следующим соотношением:
следующим соотношением:
. 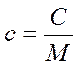
| (11.7) |
Теплоемкость, так же как и количество переданной телу теплоты, зависит от того, каким образом, а точнее при осуществлении какого процесса, теплота передавалась этому телу.
Если в процессе изменения состояния идеального газа теплоёмкость его не изменяется, то такой процесс называется политропическим.
Частными случаями политропического процесса являются рассмотренные ранее изопроцессы.
Степени свободы молекулы.
Молярная теплоемкость при постоянном объеме
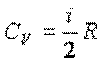 , ,
| (11.8) |
Молярная теплоемкость при постоянном давлении:
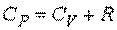 , ,
| (11.9) |
которая называется соотношением (уравнением) Майера.
 . .
| (11.10) |
Вывод уравнения Майера – самостоятельно. Источник Детлаф Яворский 2002 год. П. 9.5 С.118-122
Тепловые машины.
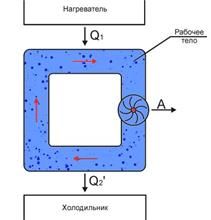
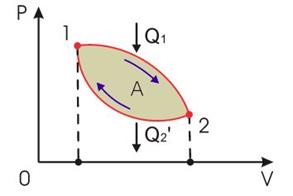
| 
| |||
| рис. 9.1 Схема тепловой машины | рис. 9.2 Цикл тепловой машины | |||
 . .
| (11.11) | |||
Тепловой коэффициент полезного действия (к.п.д.) цикла любой тепловой машины можно рассчитать как отношение полезной работы 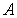 к количеству теплоты
к количеству теплоты 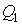 , переданной от нагревателя:
, переданной от нагревателя:
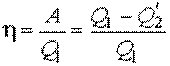 . .
| (11.12) |
к.п.д. любой тепловой машины всегда меньше единицы.
Цикл Карно
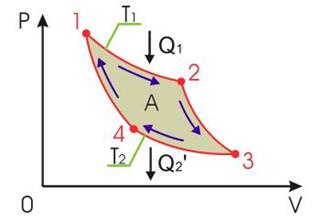
| 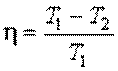 (11.13)
- К.П.Д. цикла Карно.
Коэффициент полезного действия любой обратимой тепловой машины, работающей по циклу Карно, не зависит от природы рабочего тела и устройства машины, а является функцией только температуры нагревателя (11.13)
- К.П.Д. цикла Карно.
Коэффициент полезного действия любой обратимой тепловой машины, работающей по циклу Карно, не зависит от природы рабочего тела и устройства машины, а является функцией только температуры нагревателя 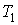 и холодильника и холодильника 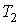 , и является максимальным. , и является максимальным.
|
| Рис. 9.3. Термодинамический цикл Карно |
Второе начало термодинамики
По Клаузиусу: "Теплота сама по себе не может перейти от более холодного тела к более теплому".
По Томсону (Кельвину): "В природе невозможен круговой процесс, единственным результатом которого была бы механическая работа, совершаемая за счет отвода теплоты от теплового резервуара".
Неравенство Клаузиуса
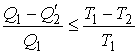 . .
| (11.14) |
Или
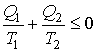
| (11.14) |
Или
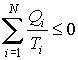 . .
| (11.15) |
Величина 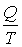 называется приведенным количеством теплоты.
называется приведенным количеством теплоты.
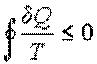 . .
| (11.16) |
Из этой формулы следует, что сумма приведенных количеств теплоты на замкнутом цикле для любой термодинамической системы не может быть больше нуля.
В случае, если термодинамический цикл состоит только из обратимых процессов, неравенство (11.16) переходит в равенство Клаузиуса
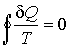 , ,
| (11.17) |
Элементарное приведенное количество теплоты 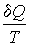 представляет собой полный дифференциал некоторой функции
представляет собой полный дифференциал некоторой функции 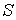 , зависящей только от состояния термодинамической системы, то есть:
, зависящей только от состояния термодинамической системы, то есть:
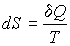 . .
| (11.18) |
Величина 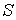 является функцией, зависящей только от равновесного состояния термодинамической системы. Она не зависит от конкретного вида термодинамического процесса, приведшего систему в указанное состояние. Эта функция была названа Клаузиусом термодинамической энтропией.
является функцией, зависящей только от равновесного состояния термодинамической системы. Она не зависит от конкретного вида термодинамического процесса, приведшего систему в указанное состояние. Эта функция была названа Клаузиусом термодинамической энтропией.
В адиабатически изолированной термодинамической системе энтропия не может убывать: она или сохраняется, если в системе происходят только обратимые процессы, или возрастает, если в системе протекает хотя бы один необратимый процесс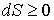 .
.
Для любой другой изолированной системы 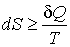
Физический смысл имеет не сама энтропия, а разность энтропий (важны только изменения состояний).
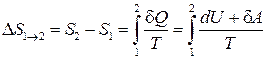 . (2.68)
. (2.68)
Изменение энтропии идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида процесса перехода.
Изоэнтропийный процесс (S=const) – это адиабатный обратимый процесс, для которого δQ = 0, поэтому ∆S =0 и, следовательно, S=const, то есть адиабатный обратимый процесс протекает при постоянной энтропии.
Дата добавления: 2017-06-02; просмотров: 462;
