Преобразования Лоренца

Принцип относительности Галилея. Преобразования Лоренца. Интервал. Релятивистские выражения для импульса и энергии.

Источник: Детлаф Яворский 2002 год Глава 7, С. 84 -100

СТО строится для ИСО - систем, по отношению к которым выполняется закон инерции.

Постулаты Эйнштейна

1. При одинаковых условиях, реализованных по отдельности в двух системах отсчета - некоторой инерциальной системы I и системы II, движущейся равномерно и прямолинейно относительно системы I - любые физические процессы в этих системах отсчета протекают одинаково.

2. В природе существует предельная (максимальная) скорость распространения физических сигналов (взаимодействий), одна и та же во всех инерциальных системах отсчета. Эта максимальная скорость совпадает со скоростью света в вакууме, она не зависит от движения источника и приемника света, и равна с = 3^.10⁸ м/с.

.
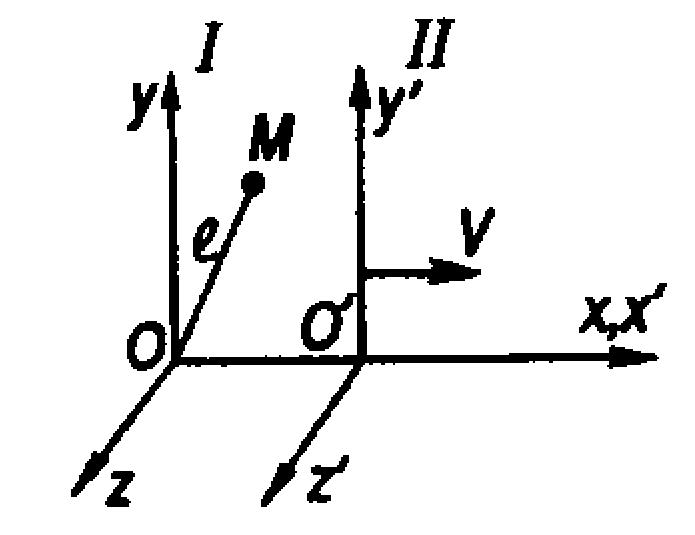
Рис. 19. 1. Относительность одновременности разноместных событий	Рис.19.2. Взаимное расположение двух движущихся инерциальных систем отсчета

Принимается условие: когда декартовы оси обеих систем I и II совмещались, базовые часы начал координат в обеих системах должны были показывать одинаковое время: t = 0 (в системе I) и также t = 0 (в системе II).

Связь между координатами и временем какого-либо события в системе I и соответствующими параметрами в системе II определяется преобразованиями Лоренца.

Преобразования Лоренца

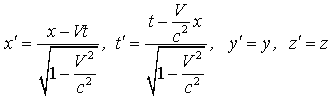Или

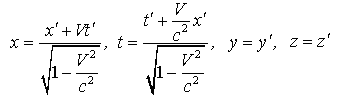
(19.1)

Следствие 1: одновременные, но происходящие в разных точках пространства, события в системе I не являются таковыми в системе II. Действительно, если 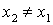, то для одного и того же t имеем

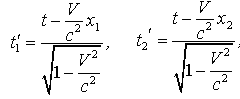
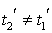(19.2)

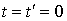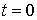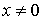Следствие 2: в момент совмещения осей систем I и II только базовые часы имеют одинаковые показания, а именно ; в любой другой точке, отличной от начал координат, показания находящихся там часов неодинаковы. Действительно, если , но , то

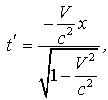в системе I 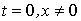, а в системе II .

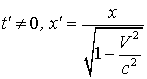Следствие 3: если 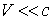, то формулы (19.1) преобразований Лоренца вырождаются и принимают вид

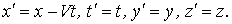
Это известные в ньютоновой механике преобразования Галилея.

Следствие 4: сокращение длины

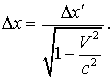(19.3)

Длина предмета в системе отсчета, в которой он покоится, называется собственной длиной (здесь - 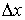). Она наибольшая. В системе, относительно которой линейка движется, она короче 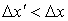, и тем короче, чем больше ее скорость V. Следовательно, длина не является понятием абсолютным (безотносительным к системам отсчета), как принимается в ньютоновой механике.

Следствие 5: Замедление времени.

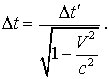(19.4)

Видно, что здесь больше, чем . В системе отсчета, в которой часы покоятся, промежуток времени наименьший. Его называют собственным временем. Иногда этот результат выражают словами: в движущемся теле процессы замедляются.