Смысл произведения и частного натуральных чисел, полученных в результате измерения величин.
Рассматривая смысл суммы и разности натуральных чисел - мер величин, мы установили, что сложение таких чисел связано со сложением величин, а вычитание - с вычитанием величин. И естественно возникает вопрос: с каким действием над величинами связано умножение и деление натуральных чисел? Чтобы ответить на него, проанализируем задачу: «Купили 3 пакета муки по 2 кг в каждом. Сколько килограммов муки купили?»
В этой задаче речь идет о массе муки, которая сначала измерена пакетами, и известно численное значение этой массы при указанной единице массы. Требуется найти результат измерения той же массы муки, но уже при помощи другой единицы - килограмм при условии, что 1 пакет - это 2 кг муки.
Рассуждения, связанные с поиском численного значения массы муки при единице - кг, можно представить в таком виде:
3 пак. =3·пак. = 3· (2кг) =3·2·кг = (3·2) кг.
Видим, что ответ на вопрос задачи находится умножением и что оно оказалось связанным с переходом (в процессе измерения массы) от одной единицы массы к другой, более мелкой.
Теорема. Если отрезок х состоит из а отрезков, длина которых равна Е, а отрезок длины Е состоит из b отрезков, длина которых равна Е1, то мера длины отрезка х при единице длины Е1 равна а·b.
Доказательство. Обозначим длину отрезка х буквой X. Но условию Х = а·Е, причем Е = b·Е1. Тогда число частей отрезка х, длина которых равна Е1, будет равно a·b, т.е. длина отрезка х при единице длины Е1 будет равна а·b.
X = a·E = a· (b·E1)=(a·b)E1.
Из этой теоремы следует, что умножение натуральных чисел, связано с переходом в процессе измерения к новой единице длины: если натуральное число а - мера длины отрезка х при единице длины Е, натуральное число b - мера длины Е при единице длины E1, то произведение а·b - это мера длины отрезка х при единице длины Е1:
a·b=mE(X) ·mEl(E)=mEl(X)
Аналогичный смысл имеет произведение натуральных чисел, полученных в результате измерения других положительных скалярных величин.
Задача 1. Объяснить смысл произведения 3 . 4, если 4 и 3 -числа, полученные в результате измерения величин.
Решение. Пусть 4 = mE(X), 3 = mEl(E), где Х - измеряемая величина, Е- первоначальная единица величины, а Е1 -новая единица величины. Тогда, согласно доказанной теореме, 4·3 = mEl(X), т.е. 4·3 - это численное значение длины X при единице длины Е1. Рассмотрим рисунок 5. Пусть Х- длина отрезка АВ. Если Е - первоначальная единица длины, то X = 4 · Е. Если Е1 - новая единица длины, такая, что Е = 3Е1, то X = 4·Е = 4 · (3·Е1) = (4·3)Е1.
Х
 |
Е
 |
Е1
Рис.5
Задача 2. Обосновать выбор действия при решении задачи.
«В одной коробке 6 ручек. Сколько ручек в трех таких коробках?»
Решение. В задаче речь идет о количестве ручек, которое сначала измерено коробками и известно численное значение этой величины при указанной единице. Требуется найти численное значение этой же величины при новой единице - ручка, причем известно, что коробка - это 6 ручек. Тогда 3 кор. = 3·кор. = 3 · (6 руч.) = 3 · (6 ·руч.) = (3 ·6) руч. Таким образом, задача решается при помощи действия умножения, поскольку в ней при измерении осуществляется переход от одной единицы величины (коробка) к другой - ручка.
Чтобы установить смысл частного натуральных чисел, полученных в результате измерения величин, рассмотрим задачу: «6 кг муки надо разложить в пакеты, по 2 кг в каждый. Сколько получится пакетов?»
В задаче рассматривается масса муки, которая сначала измерена при помощи единицы массы - килограмм, и известно численное значение этой массы при указанной единицы массы. Требуется найти результат измерения этой же массы, но уже при помощи другой единицы - пакета, причем известно, что 1 пакет - это 2 кг.
Рассуждения, связанные с поиском численного значения массы муки при новой единице - пакет, можно представить в таком виде:
6 кг = 6 ·кг = 6 ·(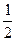 
пак.) = (6 · 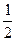) пак. = (6:2) пак.
Видим, что ответ на вопрос задачи находится делением и что оно связано с переходом (в процессе измерения) от одной единицы массы к другой, более крупной.
Теорема. Если отрезок х состоит из а отрезков, длина которых равна Е, а отрезок длины Е1 состоит из b отрезков длины Е, то мера длины отрезка х при единице длины Е1 равна а: b.
Данная теорема доказывается аналогично рассмотренной выше.
Из этой теоремы следует, что деление натуральных чисел связано с переходом в процессе измерения к новой единице длины: если натуральное число а - мера длины отрезка х при единице длины Е, а натуральное число b - мера новой единицы длины Е1 при единице длины Е, то частное а: b- это мера длины отрезка х при единице длины Е1:
а: b = mЕ(Х): mЕ(Е1) = mЕ1(Х)
Аналогичный смысл имеет частное натуральных чисел, полученных в результате измерения других положительных скалярных величин. Заметим, что такая трактовка частного возможна только для деления по содержанию.
Задача 3. Обосновать выбор действия при решении задачи.
«Из 12 м ткани сшили платья, расходуя на каждое по 4 м. Сколько платьев сшили?»
Решение. В задаче рассматривается длина ткани, которая измерена сначала при помощи единицы длины - метр, и известно численное значение заданной величины. Требуется найти численное значение той же длины при условии, что она измеряется новой единицей - платьем, причем известно, что платье - это 4 м, откуда метр - это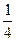 
платья.
Рассуждения, связанные с поиском численного значения длины при единице - платье, можно представить в таком виде:
12 м= 12 ·м = 12 ·( 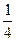пл. ] = (12· 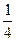)·пл. =(12:4)пл.
Таким образом, ответ на вопрос задачи находится при помощи деления, поскольку в задаче нужно перейти от одной единицы величины (метр) к другой (платье), более крупной.
Итак, умножение и деление натуральных чисел - мер величин оказалось связанным с переходом от одной единицы Величины к другой в процессе измерения одной и той же величины.
Однако выбор действий умножения и деления при решении текстовых задач с величинами можно обосновывать иначе, используя понятие умножения величины на натуральное число.
Напомним, что умножить величину А на натуральное число х - это значит получить такую величину В того же рода, что В = х·А или В=А·х, причем В = А + А + ...+А .
х слаг
Чтобы найти численное значение величины В при единице величины Е, достаточно численное значение величины А, полученное при той же единице Е, умножить на число х, т.е. если В=А·х, то mЕ(В)= mЕ(А)·х.
Рассмотрим, например, задачу: «Купили 3 пакета муки, по 2 кг в каждом. Сколько килограммов муки купили?» Чтобы ответить на вопрос задачи, надо массу 2 кг повторить слагаемым три раза, т.е. массу 2 кг умножить на число 3. Численное значение полученной при этом величины находим, умножив численное значение массы муки в одном пакете на число 3. Произведение 2-3 будет математической моделью данной задачи. Вычислив его значение, будем иметь ответ на вопрос задачи.
Если В = А·х, где х - натуральное число, В и А- величины одного рода, то с помощью деления решают две задачи:
- зная А и В, находят число х (х = В:А), причем х = mЕ(В): mЕ(А); это деление по содержанию;
- зная В их, находят А (А = В:х), причем mЕ(А) = mЕ(В):х; это деление на равные части.
С этих позиций выбор действия при решении задачи «6 кг муки разложили на пакеты по 2 кг в каждый. Сколько получилось пакетов?» можно обосновать так. В задаче надо узнать, сколько раз масса 2 кг укладывается в 6 кг, т.е. надо массу 6 кг разделить на массу 2 кг. В результате должно получиться число, которое находим, разделив численное значение одной величины на численное значение другой. Таким образом, получаем частное 6:2. Его значение и будет ответом на вопрос задачи.
Пользуясь описанным подходом к трактовке умножения и деления натуральных чисел, можно обосновывать выбор действия и при решении текстовых задач с отношениями «больше в» и «меньше в».
Задача 4. Обосновать выбор действия при решении задачи «Купили 3 кг моркови, а картофеля в 2 раза больше. Сколько килограммов картофеля купили?»
Решение. В задаче рассматриваются масса моркови и масса картофеля, причем численное значение первой массы, а численное значение второй надо найти, зная, что она в два раза больше первой.
Если воспользоваться вспомогательной моделью задачи (рис.6), то можно сказать, что масса картофеля складывается из двух масс по 3 кг, и, следовательно, численное значение можно найти, умножив 3 на 2. Найдя значение выражения 3 . 2, получим ответ на вопрос задачи.
Дата добавления: 2017-06-02; просмотров: 2786;