Модель структурного сопряжения элементов в сложных системах
Мы рассмотрели на основании использования структурных моделей сложных систем уже два уровня описания:
- наличие связей между элементами (ненаправленные графы);
- направление связей (направленные графы, пути на графах и т.д.).
Теперь рассмотрим третий уровень описания и структурного анализа сложных систем (СС) – когда учитываются состав сигналов взаимосвязи между элементами и их вид.
Для построения математической модели сопряжения элементов СС с учетом состояния и характеристик сигналов делается ряд допущений:
1) входной сигнал x(t) рассматривается как совокупность элементарных сигналов x1(t), x2(t),… xm(t), возникающих одновременно на входах элемента. Выходной сигнал y(t) – как совокупность элементарных сигналов y1(t), y2(t),… yn(t);
2) элементарные сигналы передаются в системе независимо друг от друга по элементарным каналам;
3) к входному контакту любого элемента подключается не более чем один элементарный канал;
4) к выходному контакту может быть подключено любое число элементарных каналов.
Данные допущения хорошо согласуются с характером взаимодействия элементов в реальных системах.
Итак, пусть система S состоит из N элементов.
Для i-го элемента Ci имеем X(i) – множество входных сигналов x(i), (x(i) Є X(i)), Y(i)- множество выходных сигналов y (i) ,( y (i) Є Y(i)).
Взаимодействие системы с внешней средой рассматривается как обмен сигналами между внешней средой и элементами системы. Каждый сигнал, выдаваемый во внешнюю среду, складывается из элементарных сигналов, выдаваемых одним или несколькими элементами системы. Элементарные сигналы, составляющие сигнал, который поступает из внешней среды, принимается одним или несколькими элементами.
Внешнюю среду, в этом случае, можно представить в виде фиктивного элемента системы Co, причем сигнал, выдаваемый системой во внешнюю среду, принимается внешней средой как входной сигнал x0(t)=[ xo1(t), xo2(t),… xomo(t) ], а сигнал, поступающий в систему из внешней среды, является выходным сигналом элемента, имитирующего внешнюю среду, и состоит из элементарных сигналов y0(t)=[ yo1(t), yo2(t),… yono(t) ].
Таким образом, для каждого элемента, включая и внешнюю среду, имеем множество входных контактов: [X(i)j]1mi=( X(i)1, X(i)2, X(i)3,… X(i)mi) и множество выходных контактов: [Y(i)j]1ni=( Y(i)1, Y(i)2, Y(i)3,… Y(i)ni).
Введем некоторый оператор 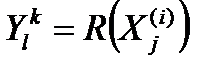 ,
,
где
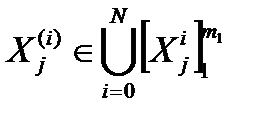 ;
; 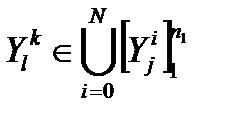 ,
,
противопоставляющий входному контакту 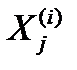 выходной контакт
выходной контакт 
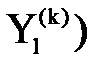 , связанный с ним элементарным каналом, причем если в системе к контакту
, связанный с ним элементарным каналом, причем если в системе к контакту 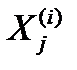 не подключен никакой элементарный канал, то оператор считается не определённым на этом
не подключен никакой элементарный канал, то оператор считается не определённым на этом 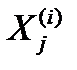 .
.
Оператор R называется оператором сопряжения. Обычно он задается в виде таблицы, в которой на пересечении строк с номерами элементов системы (i) и столбцов с номерами контактов (j) располагаются пары чисел (k,l), указывающие номер элемента (k)и номер контакта (l), с которым соединен контакт 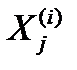 .
.
Пример1:
Система с одним уровнем иерархии (уровнем сопряжения
| Внешняя среда |
| Внешняя среда |
| Рис.1 |
Таблица, задающая оператор сопряжения R, выглядит следующим образом:
Таблица 1
| i | j | ||
| (3,1) | (4,1) | (4,2) | |
| (0,1) | (0,2) | (3,2) | |
| (0,3) | (0,4) | - | |
| (1,1) | (1,2) | - | |
| (1,3) | (2,1) | - |
Этот способ можно распространить и на многоуровневый случай, так как любую систему можно расчленить (декомпозировать) на подсистемы. При этом любая подсистема, с одной стороны, сама является системой, содержащей некоторое число элементов, а с другой – её можно рассматривать как элемент анализируемой системы S.
Подсистема Sμ как самостоятельная система должна иметь контакты Xj(o)μ и Yl(o)μ, характеризующие источники и потребители внешней среды, а как элемент системы S подсистема Sμ должна содержать входные Xj μ и выходные Ylμ контакты для связи с другими подсистемами.
Соответствующие контакты Xj(μ) и Yl(o)μ при j=l, а также Xj(o)μ и Yl(μ) при j=l объединяются в двойные контакты на границах подсистем Sμ.
Пример2:
Пусть система S состоит из двух подсистем S1 и S2, причем в подсистему S1 входят элементы C1 и C2, а в подсистему S2 – элементы C3 и C4 (рис.2).
| Внешняя среда |
| S1 |
| Внеш-няя среда |
| Рис.2 |
| S2 |
Система S1 как самостоятельная система имеет контакты
Yl(o)1,Y2(o)1,Y3(o)1,Y4(o)1,Y5(o)1; X1(o)1,X2(o)1,X3(o)1,X4(o)1;
а как элемент системы S имеет контакты
X1(1),X2(1),X3(1),X4(1),X5(1); Yl(1),Y2(1),Y3(1),Y4(1).
Аналогично соответствующие множества могут быть построены для подсистемы S2.
Введем оператор 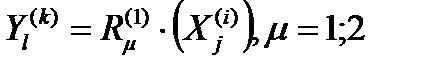 , который данному входному контакту
, который данному входному контакту 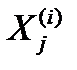 элемента Ci подсистемы Sμ ставит в соответствие выходной контакт
элемента Ci подсистемы Sμ ставит в соответствие выходной контакт 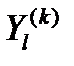 той же подсистемы, соединённый с
той же подсистемы, соединённый с 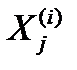 элементарным каналом (если такое соединение в подсистеме Sμ существует). Оператор
элементарным каналом (если такое соединение в подсистеме Sμ существует). Оператор 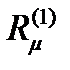 называется внутренним оператором сопряжения подсистемы Sμ (μ=1; 2). Способы задания оператора
называется внутренним оператором сопряжения подсистемы Sμ (μ=1; 2). Способы задания оператора 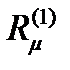 такие же, как у обычного оператора сопряжения.
такие же, как у обычного оператора сопряжения.
Операторы сопряжения 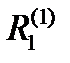 и
и 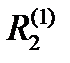 для подсистем S1 и S2 представлены соответственно в табл.2 и табл.3.
для подсистем S1 и S2 представлены соответственно в табл.2 и табл.3.
Операторы сопряжения 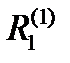 и
и 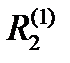 являются операторами сопряжения первого уровня.
являются операторами сопряжения первого уровня.
Таблица 2
| i | j | |||
| (1,1) | (1,2) | (1,3) | (2,1) | |
| (0,1) | (0,2) | (0,3) | - | |
| (0,4) | (0,5) | - | - |
Таблица 3
| i | j | |||
| (3,1) | (3,2) | (4,1) | (4,2) | |
| (0,1) | (0,2) | - | - | |
| (0,3) | (0,4) | - | - |
Рассмотрим теперь подсистему Sμ как элемент системы S. С этой точки зрения она характеризуется множествами входных и выходных контактов:
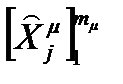 и
и 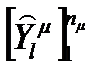 .
.
Элемент C0, представляющий внешнюю среду системы S, будем интерпретировать как подсистему S0 с входными контактами 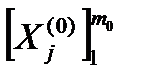 и выходными контактами
и выходными контактами 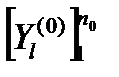 .
.
Введем оператор 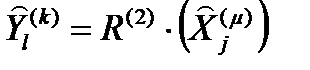 , реализующий отображение множества
, реализующий отображение множества 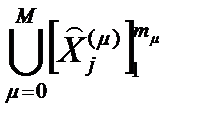 всех входных контактов подсистем S0, S1, … Sμ системы S в множество
всех входных контактов подсистем S0, S1, … Sμ системы S в множество 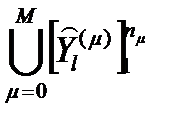 всех выходных контактов
всех выходных контактов 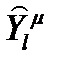 , который данному контакту
, который данному контакту 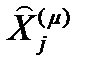 ставит в соответствие контакт
ставит в соответствие контакт 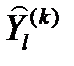 , соединенный с
, соединенный с 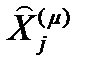 элементарным каналом (если такое соединение в системе существует).
элементарным каналом (если такое соединение в системе существует).
Оператор 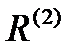 будем называть оператором сопряжения подсистем в системе S и оператором сопряжения второго уровня. Оператор сопряжения
будем называть оператором сопряжения подсистем в системе S и оператором сопряжения второго уровня. Оператор сопряжения 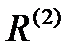 подсистем S1 и S2 и внешней среды представлен в таблице 4.
подсистем S1 и S2 и внешней среды представлен в таблице 4.
Таблица 4
| i | j | ||||
| (2,1) | (2,3) | (2,4) | - | - | |
| (0,1) | (0,2) | (2,2) | (0, 3) | (0,4) | |
| (1,1) | (1,2) | (1,3) | (1,4) | - |
0 -строка, соответствующая внешней среде;
1 - строка, соответствующая подсистеме S1;
2 - строка, соответствующая подсистеме S2 .
Совокупность внутренних одноуровневых схем сопряжения всех подсистем Sμ (μ=l,2) вместе со схемой сопряжения второго уровня называется двухуровневой схемой сопряжения системы S.
Такой подход можно развить и на случай многоуровневых систем.
| <== предыдущая лекция | | | следующая лекция ==> |
| Основные возможности MPM | | | Органы власти и управления в годы гражданской войны |
Дата добавления: 2017-06-02; просмотров: 759;
