Структура расчетных формул по предельным состояниям первой и второй групп

При расчетах по предельным состояниям первой и второй групп в качестве главного прочностного показателя материала, как уже отмечалось, устанавливается его сопротивление, которое (наряду с другими характеристиками) может принимать нормативные и расчетные значения:

R_n — нормативное сопротивление материала, представляет собой основной параметр сопротивления материалов внешним воздействиям и устанавливается соответствующими главами строительных норм (с учетом условий контроля и статистической изменчивости сопротивлений). Физический смысл нормативного сопротивления R_n — это контрольная или браковочная характеристика сопротивления материала с обеспеченностью не менее 0,95%;

R — расчетное сопротивление материала, определяется по формуле: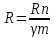

γ_m - коэффициент надежности по материалу, учитывает возможные отклонения сопротивления материала в неблагоприятную сторону от нормативных значений, γ_m > 1.

γ_c — коэффициент условий работы, учитывает особенности работы материалов, элементов и соединений конструкций, а также зданий и сооружений в целом, если эти особенности имеют систематический характер, но не отражаются в расчетах прямым путем (учет температуры, влажности, агрессивности среды, приближенности расчетных схем и др.);

N_n – нормативная нагрузка; N– расчетная нагрузка; γ_{f –} коэффициент надежности по нагрузкам, учитывает возможные отклонения нагрузок в неблагоприятную (большую или меньшую) сторону от их нормативных значений; γ_n - коэффициент надежности по ответственности, учитывает экономические, социальные и экологические последствия, которые могут возникать в результате аварий.

Соответственно, сервисная нагрузка N_sеги сервисное сопротивление R_ser считаются расчетными для расчетов по предельным состояниям второй группы.

При расчетах по первой группе предельных состояний, которые связаны с обеспечением несущей способности конструкций (здания), принимают расчетные значения: расчетные нагрузки N и расчетные сопротивления материала R.