Краткие сведения из теории подобия.

Для аналитического метода исследования конвективного теплообмена нужно решить систему дифференциальных уравнений, состоящий из:
1). Уравнения энергии (закон сохранения энергии):

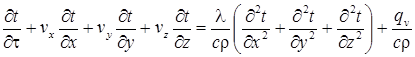, (10.4)
где: q_υ- внутренний источник тепла.
или
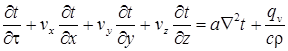, (10.5)
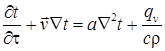(10.6)

где: 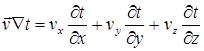. (10.7)

2). Уравнения движения (импульса):

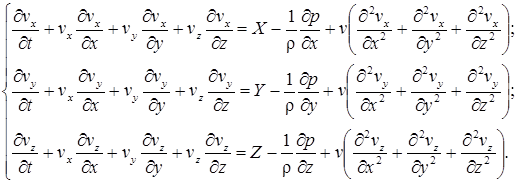(10.8)

или

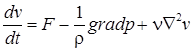. (10.9)

3). Уравнения неразрывности (закон сохранения массы):

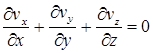. (10.10)

4). Уравнение теплообмена (условие теплообмена на границе твердого тела и среды):

α = -λ/Δt· ∂t / ∂r _n=0 . (10.11)

Данные уравнения записаны для несжимаемой жидкости (ρ = Const).

Решение этих дифференциальных уравнений сложная и трудоемкая задача, и она возможна при ограниченных простых случаев. Поэтому при исследовании конвективного теплообмена применяют метод теории подобия.
Теория подобия – это наука о подобных явлениях. Подобными явлениями называются такие физические явления, которые одинаковы качественно по форме и по содержанию, т.е. имеют одну физическую природу, развиваются под действием одинаковых сил и описываются одинаковыми по форме дифференциальными уравнениями и краевыми условиями.
Обязательным условием подобия физических явлений должно быть геометрическое подобие систем, где эти явления протекают. Два физических явления будут подобны лишь в том случае, если будут подобны все величины, которые характеризуют их.
Для всех подобных систем существуют безразмерные комплексы величин, которые называются критериями подобия.
Основные положения теории подобия формулируют в виде 3-х теорем подобия.
1 теорема: Подобные явления имеют одинаковые критерии подобия.
2 теорема: Любая зависимость между переменными, характеризую-щая какие-либо явления, может быть представлена, в форме зависимости между критериями подобия, составленными из этих переменных, которая будет называться критериальным уравнением.
3 теорема: Два явления подобны, если они имеют подобные условия однозначности и численно одинаковые определяющие критерии подобия.
Условиями однозначности являются:

• наличие геометрического подобия систем;

• наличие одинаковых дифференциальных уравнений;

• существование единственного решения уравнения пр заданных граничных условиях;

• известны численные значения коэффициентов и физических параметров.