Расчеты на устойчивость в САЕ системе

В конструкциях и сооружениях большое применение находят детали, являющиеся относительно длинными и тонкими стержнями, у которых один или два размера поперечного сечения малы по сравнению с длиной стержня. Поведение таких стержней под действием осевой сжимающей нагрузки оказывается принципиально иным, чем при сжатии коротких стержней: при достижении сжимающей силой F некоторой критической величины, равной Fкр, прямолинейная форма равновесия длинного стержня оказывается неустойчивой, и при превышении F_кр стержень начинает интенсивно искривляется (выпучивается). При этом новым (моментным) равновесным состоянием упругого длинного становится некоторая новая уже криволинейная форма. Это явление носит название потери устойчивости.

Рис. 37. Потеря устойчивости

Устойчивость – способность тела сохранять положение или форму равновесия при внешних воздействиях.

Критическая сила (F_кр) – нагрузка, превышение которой вызывает потерю устойчивости первоначальной формы (положения) тела. Условие устойчивости:

F_max ≤ F_кр, (25)

Устойчивость сжатого стержня. Задача Эйлера.

При определении критической силы, вызывающей потерю устойчивости сжатого стержня, предполагается, что стержень идеально прямой и сила F приложена строго центрально. Задачу о критической нагрузке сжатого стержня с учетом возможности существования двух форм равновесия при одном и том же значении силы решил Л. Эйлер в 1744 году.

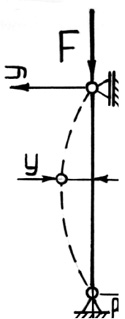
Рис. 38. Сжатый стержень

Рассмотрим шарнирно опертый по концам стержень, сжатый продольной силой F. Положим, что по какой-то причине стержень получил малое искривление оси, вследствие чего в нем появился изгибающий момент M:

M = –F•y,

где y – прогиб стержня в произвольном сечении с координатой x.

Для определения критической силы можно воспользоваться приближенным дифференциальным уравнением упругой линии:

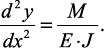(26)

Проведя преобразования, можно увидеть, что минимальное значение критическая сила примет при n = 1 (на длине стержня укладывается одна полуволна синусоиды) и J = Jmin (стержень искривляется относительно оси с наименьшим моментом инерции)

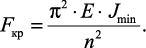(27)

Это выражение – формула Эйлера.

Зависимость критической силы от условий закрепления стержня.

Формула Эйлера была получена для, так называемого, основного случая – в предположении шарнирного опирания стержня по концам. На практике встречаются и другие случаи закрепления стержня. При этом можно получить формулу для определения критической силы для каждого из этих случаев, решая, как в предыдущем параграфе, дифференциальное уравнение изогнутой оси балки с соответствующими граничными условиями. Но можно использовать и более простой прием, если вспомнить, что, при потере устойчивости на длине стержня должна укладываться одна полуволна синусоиды.

Рассмотрим некоторые характерные случаи закрепления стержня по концам и получим общую формулу для различных видов закрепления.

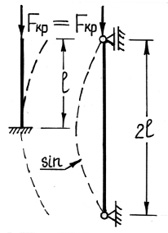
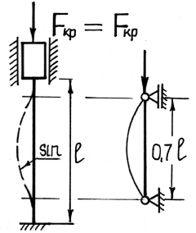
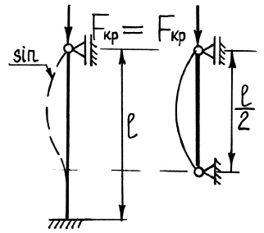
Рис. 39. Различные случаи закрепления стержня

Общая формула Эйлера:

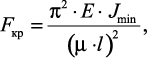(28)

где μ·l = l_пр – приведенная длина стержня; l – фактическая длина стержня; μ – коэффициент приведенной длины, показывающий во сколько раз необходимо изменить длину стержня, чтобы критическая сила для этого стержня стала равна критической силе для шарнирно опертой балки. (Другая интерпретация коэффициента приведенной длины: μ показывает, на какой части длины стержня для данного вида закрепления укладывается одна полуволна синусоиды при потере устойчивости.)

Таким образом, окончательно условие устойчивости примет вид

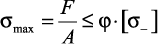(29)

Рассмотрим два вида расчета на устойчивость сжатых стержней – проверочный и проектировочный.

Проверочный расчет

Порядок проверочного расчета на устойчивость выглядит так:

– исходя из известных размеров и формы поперечного сечения и условий закрепления стержня, вычисляем гибкость;

– по справочной таблице находим коэффициент понижения допускаемого напряжения, затем определяем допускаемое напряжение на устойчивость;

– сравниваем максимальное напряжение с допускаемым напряжением на устойчивость.