Генераторы случайных и псевдослучайных последовательностей
Для генерации истинно случайных последовательностей (РРСП) используются физические генераторы.
Это электронные устройства, в которых используются естественные случайности реального мира – шумы в результате переходных процессов в полупроводниковых диодах, тепловые шумы высокомных резисторов, радиоактивный распад и т.д.
Один из принципов работы физического генератора – наблюдение событий, когда шум превышает некоторый порог.
Измерим время 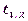 между первым событием и вторым, затем – время
между первым событием и вторым, затем – время 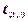 между вторым событием и третьим.
между вторым событием и третьим.
Если 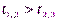 , то полагаем выход генератора равным 1; если
, то полагаем выход генератора равным 1; если 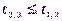 , то выход равен 0, и так далее…
, то выход равен 0, и так далее…
Существенной проблемой таких генераторов случайных данных является наличие отклонений от равновероятности и корреляций в сгенерированной последовательности.
Как с этим бороться?
А)Пусть вероятность появления нуля смещена на 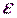 , т.е. может быть записана как
, т.е. может быть записана как 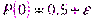 .
.
Сложение по 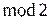 двух одинаково распределенных независимых битов даст:
двух одинаково распределенных независимых битов даст: 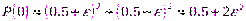 . При сложении четырех битов получим:
. При сложении четырех битов получим: 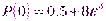 . Процесс сходится к равновероятному распределению битов.
. Процесс сходится к равновероятному распределению битов.
Б)Другой подход. Пусть распределение единиц и нулей в последовательности есть величины 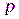 и
и 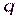 соответственно.
соответственно.
Преобразуем последовательные пары битов:
– если это одинаковые биты, то отбросим их и рассмотрим следующую пару;
– если биты различны, то в качестве выходного значения возьмем первый бит.
Данный метод позволяет решить проблему смещения, сохранив свойства случайности источника (с некоторой потерей в объеме данных).
Потенциальная проблема обоих методов в том, что при наличии корреляции между соседними битами, данные методы увеличивают смещение. Один из способов избежать этого – использовать различные источники случайных чисел и суммировать биты подписанных друг под другом последовательностей по вертикали.
Физические генераторы получили широкое распространение после создания микропроцессоров, имеющих встроенные шумовые элементы.
Физический генератор наряду с хорошими статистическими свойствами имеет ряд недостатков, к главным из которых можно отнести сложность технической реализации, невысокое быстродействие и высокую стоимость.
В силу названных причин при построении программных и программно-аппаратных средств криптографической защиты информации широкое распространение получили генераторы ПСП.
1. Наиболее простым программным датчиком псевдослучайных чисел является линейный конгруэнтный генератор (ЛКГ), который описывается рекуррентным уравнением вида 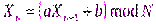 , где
, где 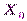 – случайное начальное значение,
– случайное начальное значение, 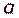 – множитель,
– множитель, 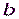 – приращение,
– приращение, 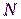 – модуль.
– модуль.
Период выходной последовательности такого генератора не превышает 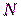 , максимальное значение достигается при правильном выборе параметров
, максимальное значение достигается при правильном выборе параметров 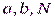 , а именно, когда:
, а именно, когда:
– числа 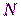 и
и 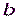 взаимно просты: НОД
взаимно просты: НОД 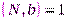 ;
;
– 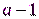 кратно любому простому
кратно любому простому 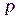 , делящему
, делящему 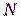 ;
;
– 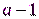 кратно 4, если
кратно 4, если 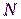 кратно 4.
кратно 4.
Для реализации ЛКГ на персональных компьютерах с учетом их разрядной сетки нередко используется модуль 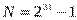
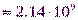 . При этом наиболее качественные статистические свойства ПСП достигаются для константы
. При этом наиболее качественные статистические свойства ПСП достигаются для константы 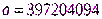 .
.
По сравнению с другими видами генераторов ПСП данный вид обеспечивает высокую производительность за счет малого числа операций для создания одного псевдослучайного бита.
Недостатком ЛКГ в плане их использования для создания поточных шифров является предсказуемость выходных последовательностей.
2. Регистры сдвига с линейной обратной связью (Linear Feedback Shift Registers – LFSR) включают собственно регистр сдвига и схему вычисления функции обратной связи (tap sequence) – см. рис. 4.2.
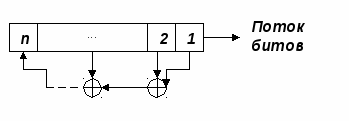
Рис. 4.2 Регистр сдвига с линейной обратной связью (LFSR)
На схеме содержимое регистра – последовательность битов – сдвигается с приходом тактового импульса (clock pulse) на один разряд вправо. Бит самого младшего разряда считается выходом LFSR в данном такте работы. Значение самого старшего разряда при этом является результатом сложения по модулю 2 (функция XOR) разрядов (точек съема) обратной связи. Генерируемая последовательность называетсялинейной рекуррентой.
Теоретически, 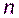 -битный LFSR может сгенерировать псевдослучайную последовательность с периодом
-битный LFSR может сгенерировать псевдослучайную последовательность с периодом 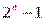 бит. Такие LFSR называютсярегистрами максимального периода.
бит. Такие LFSR называютсярегистрами максимального периода.
Для этого регистр сдвига должен побывать во всех 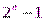 ненулевых внутренних состояниях.
ненулевых внутренних состояниях.
Одна и та же рекуррента может быть сгенерирована регистрами разной длины. Предположим, что среди подобных регистров наш 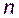 -битный LFSR обладает минимальной длиной.
-битный LFSR обладает минимальной длиной.
Функции обратной связи регистра можно сопоставить полином 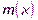 степени не выше
степени не выше 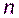 с коэффициентами из поля вычетов по модулю два, состоящий из одночленов вида
с коэффициентами из поля вычетов по модулю два, состоящий из одночленов вида 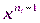 , где
, где 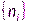 - множество номеров точек съема обратной связи.
- множество номеров точек съема обратной связи.
Полином 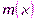 называется минимальным полиномом соответствующей рекуррентной последовательности.
называется минимальным полиномом соответствующей рекуррентной последовательности.
Для каждой конечной (или периодической) последовательности 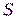 можно указать LFSR, который, при некотором начальном заполнении, порождает эту последовательность.
можно указать LFSR, который, при некотором начальном заполнении, порождает эту последовательность.
Среди всех таких регистров, существует регистр минимальной длины 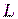 .
.
Величина 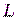 называется линейной сложностью последовательности
называется линейной сложностью последовательности 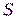 .
.
Напомним, что полином называется неприводимым, если он не может быть выражен как произведение двух полиномов меньшей степени, отличных констант.
Примитивный полином степени 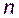 над полем вычетов по модулю два – это неприводимый полином, который делит
над полем вычетов по модулю два – это неприводимый полином, который делит 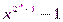 , но не делит
, но не делит 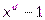 для любых
для любых 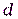 :
: 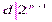 .
.
Теорема. Для того, чтобы последовательность, порожденная LFSR имела максимальный период, необходимо и достаточно, чтобы ее минимальный полином, был примитивным полиномом по модулю 2.
Например, примитивным полиномом является 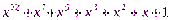 .
.
Вообще говоря, LFSR – удобны для технической реализации, но с точки зрения криптографической стойкости, обладают слабостями.
Последовательные биты линейной рекурренты линейно зависимы, что делает их бесполезными для шифрования.
Достаточно 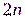 последовательных битов рекурренты, чтобы определить множество номеров точек съема обратной связи.
последовательных битов рекурренты, чтобы определить множество номеров точек съема обратной связи.
Большие случайные числа, сгенерированные из последовательных битов LFSR, сильно коррелированны. Тем не менее, LFSR достаточно часто используются в качестве элементов более сложных алгоритмов формирования шифрующей ключевой последовательности.
Наиболее эффективные решения были получены на основе составных генераторов.
В случае создания криптографически стойкого генератора ПСП легко решается вопрос создания потоковых шифров. Выход таких ПСП неотличим (точнее, должен быть неотличим) от РРСП. Два генератора всегда могут быть синхронно запущены из одного вектора начального состояния, который намного короче передаваемого сообщения, что выгодно отличает эту схему от шифра Вернама.
Существуют 2 основных подхода к конструированию соответствующих генераторов:
1) системно-теоретический подход;
2) сложностно-теоретический подход;
При системно-теоретическом подходе генератор конструируется таким образом, чтобы он обладал поддающимися проверке свойствами, включая длину периода выходной последовательности, статистическое распределение потока бит, линейную сложность выходной последовательности и т.д.
На основе такого подхода Рюппелем сформулирован следующий набор критериев для таких генераторов:
1.Большой период выходной последовательности, отсутствие повторений.
2. Высокая линейная сложность выходной последовательности.
3. Неотличимость от РРСП по статистическим критериям.
4. Перемешивание: любой бит выходной последовательности должен быть сложным преобразованием всех или большинства бит начального состояния.
5. Рассеивание: изменение одного бита начального состояния должно кардинально изменять выходную последовательность.
6. Критерий нелинейности: биты выходной последовательности должны быть функциями высокой степени нелинейности от бит начального состояния.
Примером удачного построения составного генератора с точки зрения повышения линейной сложности является каскад Голмана (рис. 4.3). Каскад Голмана включает несколько регистров сдвига LFSR. Первый регистр движется равномерно с шагом 1. Сдвиг каждого последующего регистра управляется предыдущим так, что изменение состояния последующего регистра в такте 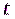 происходит, если в такте
происходит, если в такте 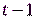 с предыдущего регистра снимается 1. Иначе, состояние последующего регистра не изменяется.
с предыдущего регистра снимается 1. Иначе, состояние последующего регистра не изменяется.
Если все LFSR – длины 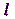 , то линейная сложность системы с
, то линейная сложность системы с 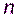 регистрами равна
регистрами равна 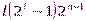 .
.

Рис. 4.3. Каскад Голлмана
Типичным примером комбинирования регистров сдвига является схема чередующегося «старт-стоп» генератора (Alternating Stop-and-Go Generator).
У этого генератора большой период и большая линейная сложность.
В «старт-стоп» генераторе (рис. 4.4) используется три линейных регистра сдвига различной длины. LFSR-2 меняет состояние, если выход LFSR-1 равен 1; LFSR-3 меняет состояние в противном случае. Результат генератора есть сложение по модулю 2 выходов регистров LFSR-2, LFSR-3.
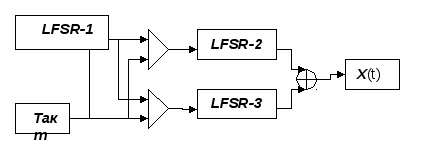
Рис. 4.4. Чередующийся старт-стопный генератор
При сложностно-теоретическом подходе стойкость генератора, доказывается, используя теорию сложности.
Основу решений при этом подходе составляют генераторы, базирующиеся на понятии однонаправленной функции.
Примером однонаправленной функции является показательная функция в некотором конечном поле 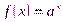 , где
, где 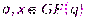 .
.
Нетрудно видеть, что возведение в степень можно ускорить за счет свойств ассоциативности. Например, 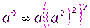 , что позволяет вычислить степень за четыре шага, вместо восьми.
, что позволяет вычислить степень за четыре шага, вместо восьми.
Обратная операция – задача нахождения показателя степени по значению степенной функции (дискретный логарифм), в общем случае, пока не может быть решена лучше, чем с помощью оптимизированных методов перебора.
Примером генераторана основе однонаправленной функции может служить генератор на основе алгоритма RSA с параметрами 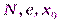 вида
вида 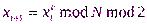 .
.
Здесь 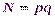 , где
, где 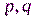 – секретные большие, неравные простые числа,
– секретные большие, неравные простые числа,
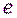 – показатель степенной функции, НОД
– показатель степенной функции, НОД 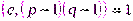 ,
, 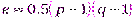 .
.
Результат работы одного такта генератора – младший бит 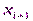 . Стойкость этого генератора не ниже стойкости RSA. Если
. Стойкость этого генератора не ниже стойкости RSA. Если 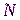 достаточно большое, то генератор обеспечивает практическую стойкость.
достаточно большое, то генератор обеспечивает практическую стойкость.
BBS-генератор. Математическая теория этого генератора – квадратичные вычеты по составному модулю 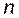 .
.
Параметры генератора: секретные большие, неравные простые числа, 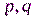 , такие, что,
, такие, что, 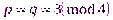 ; число
; число 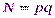 ;
; 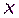 – случайный секретный вычет по модулю
– случайный секретный вычет по модулю 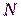 .
.
Первым шагом вычисляется начальное состояние 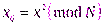 .
.
В основном цикле елемент ПСП з номером 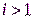 равен
равен 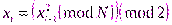 , т.е
, т.е 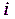 -ым псевдослучайным числом является младший бит числа
-ым псевдослучайным числом является младший бит числа 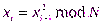 .
.
Заметим, что алгоритм можно использовать для шифрования файлов с произвольным доступом, если, кроме 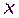 , ввести секретный параметр
, ввести секретный параметр 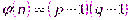 , поскольку тогда
, поскольку тогда 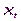 можна вычислять через
можна вычислять через 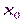 , потому, что
, потому, что 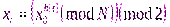 , где
, где 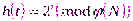 .
.
В заключение отметим, что для построения генератора ПСП необходимо получить несколько случайных битов. Наиболее простой способ: использовать наименьший значимый бит таймера компьютера.
Асимметричные системы шифрования
Шифрование и дешифрование базируются на использовании ключей. Математически это можно выразить следующим образом
EK(M) = C DK(c) = M, где K – ключ, M – исходный текст; C – зашифрованный текст.
Асимметричные схемы шифрования/дешифрования предполагают существования независимых ключей для шифрования и дешифрования. Причем один не может быть получен из другого и наоборот. В идеале ключ дешифровки не может быть получен из шифрующего ключа за любое разумное время. В этом случае ключ шифрования может быть сделан общедоступным (например, алгоритм RSA). Партнеры до начала коммуникаций должны послать друг другу ключи шифрования КШО и КШП (ключи шифрования отправителя и получателя). Возможность перехвата таких ключей опасности не представляет. Дешифрование выполняется с помощью ключей КДО и КДП, которые образуют пары с КШО и КШП соответственно и формируются совместно. Ключи КШО и КШП обычнопересылаются на фазе инициализации сессии информационного обмена.
Большинство ассиметричных алгоритмов шифрования них базируются на методах, заимствованных из теории чисел. По этой причине, прежде чем переходить к следующему разделу, введем некоторые определения.
Конгруентность (сравнимость). a конгруентно b по модулю n (a º nb), если при делении на n a и b, получается идентичный остаток. Так 100 º 1134 (100 и 34 при делении на 11 дают остаток 1) и –6 º 810 (ведь –6 =8(-1)+2). Мы всегда имеем a º nbдля некоторого 0 £ b£ n-1. Если a ºnb и сº d,то справедливы равенства:
a +c º n(b + d) и ac ºnbd
Аналогичная процедура для деления не всегда справедлива: 6º 1218 но 3¹ 9.
Наибольший общий делитель (НОД). Для a и b число (a,b) является наибольшим общим делителем, который делит a и b без остатка:
(56,98)=14; (76,190)=38
Теорема 1. Для любых a,b существуют целые числа x,y, для которых ax+by=(a,b).
В этом можно убедиться, решая уравнение 30x+69y=3 путем последовательных упрощающих подстановок (ищется целочисленное решение):
30x+69y=3
Легко видеть, что x"=1, y'=0 является решением окончательного уравнения. Мы можем получить решение исходного уравнения путем обратной подстановки. x'=x"-3y'=1 y=y'-3x'=-3 x=x'-1y=7 Мы можем решить уравнение вида 30x+69y=15 путем умножения нашего решения: y=-15, x=35. Должно быть ясно, что уравнение не будет иметь целочисленного решения, если 15 заменить на что-то некратное (30,69)=3. Все другие целочисленные решения 30x+69y=15 могут быть получены, варьируя первое решение: y=-15+(30/3)t x=35 –(69/3)t для целого t Если мы проделаем то же для произвольного равенства ax+by=(a,b), мы возможно получим один из коэффициентов равным нулю, а другой – (a,b). В действительности эта процедура представляет собой алгоритм Евклида для нахождения наибольшего общего делителя. Важно то, что этот процесс реализуем на ЭВМ даже в случае, когда a и b имеют несколько сотен значащих цифр. Легко показать, что 600-значное число не потребует более чем 4000 уравнений. Теорема 1 справедлива и для простых чисел.
Во многих криптографических приложениях используется: a a2 a3 … mod p, где a и p целые числа. Оказывается, можно выполнить такие вычисления даже для случая, когда в указанную процедуру вовлечены достаточно большие числа, например: |
Mod 987.
Фокус заключается в том, что берется число и осуществляется возведение в квадрат.
4322 = 186624; 186624 mod 987 = 81; 4324 mod 987 = 812 mod 987 = 639
4328 -> 6392 mod 987 -> 690 …. 432512 -> 858
так как 678= 512+128+32+4+2, то:
432678->(81)(639)….(858) -> 204
Вычисления с использованием показателя включают в себя ограниченное число умножений. Если числа содержат несколько сотен цифр, необходимы специальные подпрограммы для выполнения таких вычислений. Рассмотрим последовательность степеней 2n mod 11:
2 4 8 5 10 9 7 3 6 1
Здесь числа от 1 до 10 появляются в виде псевдослучайной последовательности.
Теорема 2
Пусть p является простым числом. Существует такое a, что для каждого 1£ b £ p-1
существует такое1£ x £ p-1, что axº pb.
Степени 2 mod 7 равны 2, 4, 1. Далее числа повторяются, а числа 3, 5, или 6 не могут быть получены никогда. Рассмотрим некоторые следствия этой теоремы.
Следствие 4.Пусть a соответствует требованиям теоремы 2, тогда ap-1 º p1.
Следствие 5.Для любого b ¹ 0, bp-1 º p1.
Следствие 6. Если x º (p-1)y, тогда bx º pby
Лемма
Пусть b ¹ 0, d наименьшее положительное число, такое что bd ºp1. Тогда для любогос>0cbc ºp1 dделит c без остатка. В частности для следствия5, dделитp-1без остатка.
Согласно теореме 2, если p простое число, существует такое a, при котором равенство ax º pb имеет решение для любогоb¹ 0.Такое значениеaназываетсяпримитивным корнем p, а x называется дискретным логарифмом b. Получение b при заданных a и x относительно просто, определение же x по a и b заметно сложнее. Многие современные системы шифрования основываются на факте, что никаких эффективных путей вычисления дискретных логарифмов не найдено. Никакого эффективного метода определения примитивных корней также неизвестно. Однако часто возможно найти примитивные корни в некоторых специальных случаях. Возьмем p=1223. p-1=2*13*47. Согласно лемме, если a не примитивный корень, тогда мы либо имеем a26, a94 или
a611 º 12231. a=2иa=3не годятся, ноa=5соответствует всем трем условиям, таким образом, это значение является примитивным корнем. Мы могли бы сказать, что a=4 не может быть признано примитивным корнем без проверки.
Легко показать, что если a примитивный корень, ax примитивный корень в том и только том случае, если (x,p-1)=1. В этом примере это означает, что число примитивных корней равно
1222*(1/2)*(12/13)*(46/47)=552
Таким образом, если мы выберем а произвольно, вероятность того, что это будет примитивный корень равна ~.45. Выбирая а наугад и тестируя, можно сравнительно быстро найти примитивный корень.
Современные системы шифрования используют асимметричные алгоритмы с открытым и секретным ключами, где нет проблемы безопасной транспортировки ключа. К числу таких систем относится алгоритм rsa (rivest-shamir-adleman - разработчики этой системы – Рональд Ривест, Ади Шамир и Леонард Адлеман, 1977 год), базирующийся на разложение больших чисел на множители.
Другие сходные алгоритмы используют целочисленные логарифмы и вычисление корней уравнений. В отличие от других систем эти позволяют кроме шифрования эффективно идентифицировать отправителя (электронная подпись). К системам с открытым ключом предъявляются следующие требования:
- шифрованный текст трудно (практически невозможно) расшифровать с использованием открытого ключа.
- восстановление закрытого ключа на основе известного открытого должно быть нереализуемой задачей на современных ЭВМ. При этом должна существовать объективная оценка нижнего предела числа операций, необходимых для решения такой задачи.
К сожалению, эти алгоритмы достаточно медленно работают. По этой причине они могут использоваться для транспортировки секретных ключей при одном из традиционных методов шифрования-дешифрования.
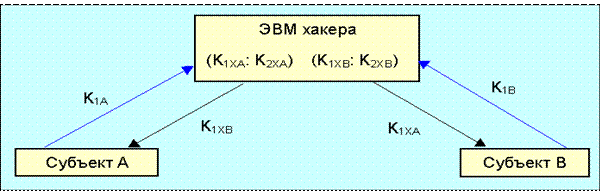 Рис.1
Если хакер умудрится вставить свою ЭВМ в разрыв канала, соединяющего субъектов А и В, у него появляется возможность перехватывать в том числе и шифрованные сообщения. Пусть субъект А сформировал пару ключей К1А и К2А (ключ с индексом 2 является секретным), аналогичную пару ключей сгенерировал субъект В (К1В и К2В). Хакер же тем временем подготовил две пары ключей (К1ХА:К2ХА и К1ХВ:К2ХВ). Когда субъект А пошлет открытый ключ К1Асубъекту В, хакер его подменит ключом К1ХА. Аналогичную процедуру он проделает с ключом К1В, посланным от В к А. Теперь сообщение А к В, зашифрованное с помощью ключа К1ХА будет послано В. Хакер его перехватывает, дешифрует с помощью ключа К2ХА, шифрует с помощью ключа К1ХВ и посылает В. СубъектВ, получив послание, дешифрует его с помощью "секретного" ключа К2ХВ, полученного от хакера (о чем он, естественно, не подозревает). Аналогичная процедура будет проведена и при посылки сообщения от В к А. В сущности единственным параметром который изменится существенным образом будет время доставки сообщения, так как это время будет включать дешифровку и повторную шифровку сообщения. Но при использовании быстродействующей ЭВМ и при работе с традиционной электронной почтой это может оказаться незаметным. Понятно, что между А и В появится дополнительный шаг (hop). Но и это может быть легко замаскировано под прокси сервер или Firewall.
Решить эту проблему можно путем пересылки открытого ключа своему партнеру по какому-то альтернативному каналу или сверки его по телефону.
Рис.1
Если хакер умудрится вставить свою ЭВМ в разрыв канала, соединяющего субъектов А и В, у него появляется возможность перехватывать в том числе и шифрованные сообщения. Пусть субъект А сформировал пару ключей К1А и К2А (ключ с индексом 2 является секретным), аналогичную пару ключей сгенерировал субъект В (К1В и К2В). Хакер же тем временем подготовил две пары ключей (К1ХА:К2ХА и К1ХВ:К2ХВ). Когда субъект А пошлет открытый ключ К1Асубъекту В, хакер его подменит ключом К1ХА. Аналогичную процедуру он проделает с ключом К1В, посланным от В к А. Теперь сообщение А к В, зашифрованное с помощью ключа К1ХА будет послано В. Хакер его перехватывает, дешифрует с помощью ключа К2ХА, шифрует с помощью ключа К1ХВ и посылает В. СубъектВ, получив послание, дешифрует его с помощью "секретного" ключа К2ХВ, полученного от хакера (о чем он, естественно, не подозревает). Аналогичная процедура будет проведена и при посылки сообщения от В к А. В сущности единственным параметром который изменится существенным образом будет время доставки сообщения, так как это время будет включать дешифровку и повторную шифровку сообщения. Но при использовании быстродействующей ЭВМ и при работе с традиционной электронной почтой это может оказаться незаметным. Понятно, что между А и В появится дополнительный шаг (hop). Но и это может быть легко замаскировано под прокси сервер или Firewall.
Решить эту проблему можно путем пересылки открытого ключа своему партнеру по какому-то альтернативному каналу или сверки его по телефону.
| <== предыдущая лекция | | | следующая лекция ==> |
| Служебные файлы NTFS | | | СТАЦИОНАРНАЯ ПОМОЩЬ |
Дата добавления: 2017-05-18; просмотров: 2523;
