Эффективное кодирование неравновероятных символов сообщений
В случае, если символы кодируемого сообщения неравновероятны, в общем виде правило получения оптимального эффективного кода неизвестно. Однако из общих соображений можно представить принципы его построения.
Очевидно, что эффективное кодирование будет оптимальным, если неравномерное распределение вероятностей появления символов алфавита источника сообщений с помощью определенным образом выбранного кода переводят в равновероятное распределение вероятностей появления независимых элементов кодовых символов. В этом случае среднее количество информации, приходящееся на один элемент символа кода, будет максимальным. Для определения вида кода, удовлетворяющего этому требованию, можно рассмотреть «функцию стоимости» (цены передачи символов сообщения) в виде:
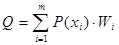 , (2.5)
, (2.5)
где P(xi) — вероятность появления i-го символа алфавита исходного кодируемого сообщения;
m — объем алфавита;
Wi — стоимость передачи i-го символа алфавита, которая пропорциональна длине кодового слова.
Эффективный код должен минимизировать функцию Q. Если передача всех элементов символов кода имеет одинаковую стоимость, то стоимость кодового символа будет пропорциональна длине соответствующего кодового символа. Следовательно, в общем случае (при неравновероятных символах исходного сообщения) код должен быть неравномерным, поэтому построение эффективного кода должно основываться на следующих принципах:
1. Длина кодового символа (ni)должна быть обратно пропорциональна вероятности появления соответствующего символа исходного кодируемого сообщения (xi);
2. Начало более длинного кодового символа не должно совпадать с началом более короткого (для возможности разделения кодовых символов без применения разделительных знаков);
3. В длинной последовательности элементы символов кода должны быть независимы и равновероятны.
Теоретическое обоснование возможности эффективного кодирования передаваемых по каналу сообщений обеспечивает теорема, доказанная К. Шенноном и которая носит название первая теорема Шеннона или основная теорема Шеннона о кодировании для каналов без помех. Эта теорема гласит, что если источник сообщений имеет энтропию Н [бит/символ], а канал обладает пропускной способностью С [бит/сек] (пропускная способность характеризует максимально возможное значение скорости передачи информации), то всегда можно найти способ кодирования, который обеспечит передачу символов сообщения по каналу со средней скоростью
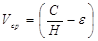 [символ/сек],
[символ/сек],
где ε — сколь угодно малая величина.
Обратное утверждение говорит, что передача символов сообщения по каналу со средней скоростью Vср. > Н невозможна и, следовательно,
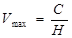 [символ/сек].
[символ/сек].
Эта теорема часто приводится в иной формулировке: сообщения источника сообщений с энтропией Н всегда можно закодировать последовательностями элементов кодовых символов с объемом алфавита k так, что среднее число элементов символов кода на один символ кодируемого сообщения (l ср. ) будет сколь угодно близко к величине H / log2 k, но не менее ее.
Не вдаваясь в доказательство этой теоремы, отметим, что эта теорема показывает возможность наилучшего эффективного кодирования, при котором обеспечивается равновероятное и независимое поступление элементов символов кода, а следовательно, и максимальное количество переносимой каждым из них информации, равное log2 k (бит/элемент) . К сожалению, теорема не указывает конкретного способа эффективного кодирования, она лишь говорит о том, что при выборе каждого элемента кодового символа необходимо чтобы он нес максимальное количество информации, а, следовательно, все элементы символов кода должны появляться с равными вероятностями и взаимнонезависимо.
Исходя из изложенных принципов, разработаны ряд алгоритмов эффективного кодирования как для взаимнонезависимых символов сообщения, так и для взаимнозависимых. Суть их состоит в том, что они сокращают среднюю длину кодовых символов путем присвоения кодовых символов минимальной длины символам исходного сообщения, которые встречаются наиболее часто.
2.5. Алгоритмы эффективного кодирования неравновероятных взаимнонезависимых символов источников сообщений
Алгоритм Шеннона-Фено. Суть этого алгоритма, при использовании двоичного кода (объем алфавита элементов символов кода равен 2), заключается в следующем.
Все символы алфавита источника сообщений ранжируют, т. е. располагают в порядке убывания вероятностей их появления. Затем символы алфавита делятся на две группы приблизительно равной суммарной вероятности их появления. Все символы первой группы получают «0» в качестве первого элемента кодового символа, а все символы второй группы — «1». Далее группы делятся на подгруппы, по тому же правилу примерно равных суммарных вероятностей, и в каждой подгруппе присваивается вторая позиция кодовых символов. Процесс повторяется до закодирования всех символов алфавита кодируемого источника сообщений. В кодовый символ, соответствующий последней группе, добавляется в качестве последнего элемента «0» для того, чтобы начальный элемент символов кода не совпадал с конечным, что позволяет исключить разделительные элементы между символами кода.
Таблица 2.2 иллюстрирует процесс построения кода Шеннона–Фено на примере источника сообщений, алфавит которого состоит из восьми символов.
Таблица 2.2
| Номер | Символы | Вероятности | Номера | Кодовые |
| символа. (i) | алфавита. (mi) | (Рi). | Разбиений. | Символы. |
| m1 | 1/2 | I II III IV V VI VII | ||
| m2 | 1/4 | |||
| m3 | 1/8 | |||
| m4 | 1/16 | |||
| m5 | 1/32 | |||
| m6 | 1/64 | |||
| m7 | 1/128 | |||
| m8 | 1/256 |
На рис. 2.1 представлен граф кодирования (кодовое дерево), который показывает, как «расщепляется» ранжированная последовательность символов кодируемого источника сообщений на группы и отдельные символы и какие кодовые символы присваиваются группам и отдельным символам алфавита источника сообщений на каждом шаге разбиения.
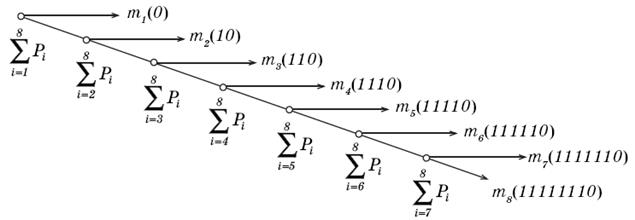
Рис 2.1. Граф кодирования по алгоритму Шеннона–Фено.
Алгоритм Шеннона–Фено применим и при иных числовых основаниях кода (k > 2). В этом случае алгоритм получения кода аналогичен рассмотренному примеру, только алфавит кодируемого источника сообщений разбивается на k групп и подгрупп примерно одинаковой суммарной вероятности.
Представляет интерес сравнение эффективного кодирования равномерным кодом и неравномерным кодом по алгоритму Шеннона–Фено.
В качестве примера рассмотрим предложенный выше (Табл. 2.2) источник сообщений с объемом алфавита равным 8 и соответствующими вероятностями появления отдельных символов (Pi). Для кодирования используем двоичный код ( k = 2).
Энтропия рассмотренного источника сообщений (Hи) определяется по формуле Шеннона:
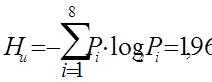 (бит/символ).
(бит/символ).
Максимально же возможное значение энтропии источника сообщений (Hu.max), при условии равновероятного и взаимно независимого появления символов, находится по формуле Хартли:
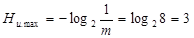 .
.
Следовательно, избыточность рассматриваемого источника сообщений (Rи) может быть найдена из соотношения:
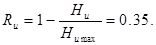
Используя формулу для эффективного равномерного кода (2.4) при k = 2, получим значность равномерного двоичного кода (пр):
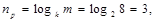
и избыточность равномерного кода (Rрк):
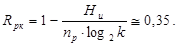
Энтропия элементов символов равномерного кода 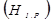 , т.е. количество информации, приходящееся на один элемент символа кода, будет равна:
, т.е. количество информации, приходящееся на один элемент символа кода, будет равна:
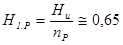 (бит / элемент символа кода). (2.6)
(бит / элемент символа кода). (2.6)
При использовании эффективного кодирования по алгоритму Шеннона-Фено соответствующие информационные параметры кода будут следующие.
Средняя длина неравномерного кода (пН) определяется выражением:
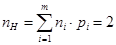 , (2.7)
, (2.7)
где пi — значность i - го кодового символа, соответствующего символу алфавита mi.
Избыточность неравномерного кода (RНК) определим из соотношения:
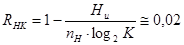
Энтропия элементов символов эффективного неравномерного кода 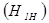 может быть легко найдена:
может быть легко найдена:
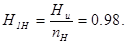 (бит/элемент символа кода). (2.8)
(бит/элемент символа кода). (2.8)
Из сравнения выражений (2.6) и (2.8) видно, что, при использовании эффективного кодирования по алгоритму Шеннона-Фено, энтропия элементов символов такого неравномерного кода на 50% выше чем энтропия элементов символов в случае использования равномерного кода. Если предположить, что скорость передачи по каналу элементов символов кода (W) одинакова для равномерного и неравномерного кода, то скорость передачи информации (V), определяемая выражением
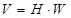 ,
,
где Н — энтропия элементов символа кода,
также будет на 50% выше при использовании эффективного кодирования по алгоритму Шеннона–Фено по сравнению с равномерным кодированием.
Алгоритм Шеннона–Фено часто применяют и для блочного кодирования. При этом также существенно повышается эффективность кодирования. Для иллюстрации такого кодирования рассмотрим процедуру эффективного кодирования двоичным числовым кодом сообщений, генерируемых источником сообщений с объемом алфавита равным 2 (m = 2), т.е. с алфавитом, состоящим только из двух символов m1 и m2 с вероятностями появления P(m1) = 0,9 и P(m2) = 0,1 и, следовательно, с энтропией Н = 0,47.
При посимвольном кодировании по алгоритму Шеннона–Фено эффект отсутствует, так как на каждый символ сообщения будет приходится один символ кода, состоящий из одного элемента.
Произведем теперь кодирование по алгоритму Шеннона–Фено блоков, состоящих из комбинаций двух символов источника сообщений, считая символы взаимнонезависимыми. Результат приведен в таблице 2.3.
Таблица 2.3.
| Блоки | Вероятности | Номера разбиений | Кодовые комбинации |
| m1m1 m1m2 m2m1 m2m2 | 0,81 0,09 0,09 0,01 | I II III |
Среднее число элементов символов кода на один символ исходного сообщения, вычисленное по формуле (2.7), равно 0,645, что значительно ниже, чем при посимвольном кодировании.
Кодирование блоков, соответствующих комбинациям из трех символов источника сообщений, дает еще больший эффект. Результат приведен в таблице 2.4.
Таблица 2.4.
| Блоки. | Вероятности. | Номера разбиений. | Kодовые комбинации. |
| m1 m1 m1 | 0,729 | I | |
| m2 m1 m1 | 0,081 | III | |
| m1 m2 m1 | 0,081 | II | |
| m1 m1 m2 | 0,081 | IV | |
| m2 m2 m1 | 0,009 | VI | |
| m2 m1 m2 | 0,009 | V | |
| m1 m2 m2 | 0,009 | VII | |
| m2 m2 m2 | 0,001 |
В этом случае среднее число элементов символов кода на один символ исходного источника сообщений равно 0,53.
Теоретический минимум Н = 0,47 может быть достигнут при кодировании блоков неограниченной длины.
Алгоритм Шеннона-Фено не всегда приводит к однозначному построению кода, так как при разбиении на подгруппы можно сделать большей по суммарной вероятности как верхнюю, так и нижнюю подгруппу. Этого недостатка лишен алгоритм Хаффмена, который гарантирует однозначное построение эффективного кода.
Алгоритм Хаффмена.Суть этого алгоритма, при использовании двоичного кода, состоит в следующем. Все символы алфавита источника сообщений ранжируют, т.е. выписывают в столбец в порядке убывания вероятностей их появления. Два последних символа объединяют в один вспомогательный символ, которому приписывают суммарную вероятность.
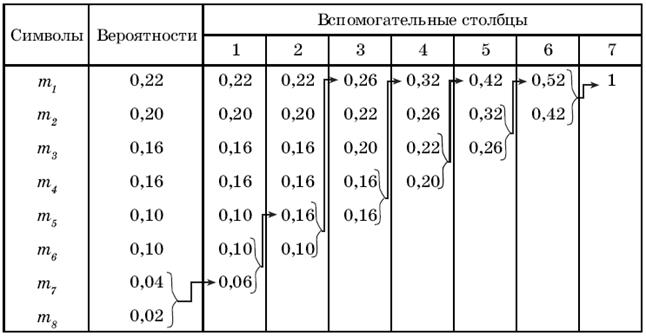
Вероятности символов, не участвовавших в объединении, и вероятность вспомогательного символа вновь ранжируют, т.е. располагают в порядке убывания вероятностей в дополнительном столбце и два последних символа объединяются. Процесс продолжается до тех пор, пока не получим единственный вспомогательный символ с вероятностью равной единице. Пример кодирования по алгоритму Хаффмена приведен в таблице 2.5.
Таблица 2.5
На рис. 2.2 показан граф кодирования (кодовое дерево), который иллюстрирует ранжирование символов на группы и отдельные символы, причем из точки, соответствующей вероятности 1, направляем две ветви: одной из них (с большей вероятностью) присваиваем символ 1, а второй – символ 0.
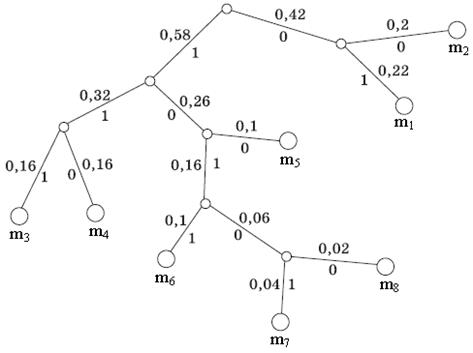 Рис 2.2. Граф кодирования по алгоритму Хаффмена .
Рис 2.2. Граф кодирования по алгоритму Хаффмена .
| Такое последовательное ветвление продолжим до тех пор, пока не дойдем до вероятности каждого символа. Двигаясь по кодовому дереву сверху вниз, можно записать для каждого символа источника сообщений соответствующую ему комбинацию (кодовый символ). |
Различные символы, генерируемые источником сообщения, и соответствующие им кодовые символы представлены в таблице 2.6.
Таблица 2.6.
| m1 | m2 | m3 | m4 | m5 | m6 | m7 | m8 |
Этот алгоритм можно использовать и при ином числовом основании кода, а также использовать блоки, как это рассмотрено в алгоритме Шеннона-Фено.
Эффективность рассмотренных алгоритмов достигается благодаря присвоению более коротких кодовых комбинаций (кодовых символов) символам источника сообщений, вероятность которых более высока, и более длинных кодовых комбинаций - символам источника сообщений с малой вероятностью. Это ведет к различиям в длине кодовых символов и, как следствие, к трудностям при их декодировании. Для разделения отдельных кодовых символов можно использовать специальный разделительный элемент, но при этом существенно снижается эффективность кода, т.к. средняя длина кодового символа фактически увеличивается на один элемент символа кода.
Целесообразнее обеспечить декодирование без введения дополнительных элементов символов. Этого можно добиться, если в эффективном коде ни одна кодовая комбинация не будет совпадать с началом более длинной кодовой комбинации. Коды, удовлетворяющие этому условию, называют префиксными кодами (префиксом или началом называют первый элемент в кодовом символе, а последний элемент – окончанием или постфиксом).
Легко заметить, что коды, построенные по алгоритмам Шеннона–Фено или Хаффмена, являются префиксными.
Дата добавления: 2017-05-18; просмотров: 2491;
