Энтропия непрерывных сообщений.

В приведенных выше рассуждениях предполагалось, что все возможные значения (символы) непрерывного сообщения равновероятны, однако это не всегда справедливо. Как правило, символы непрерывного сообщения х(t) обладают некоей плотностью распределения вероятности р(х), которая характеризует вероятность попадания символов непрерывного сообщения х(t) в интервал ∆х, примыкающий к точке х. И, если плотностью распределения вероятности значений непрерывного сообщения р(х), не постоянна, то и вероятность появления отдельных символов непрерывного сообщения различна. Следовательно, в соответствии с формулой (1.4), количество информации, которое может нести отдельный символ непрерывного сообщения, так же не постоянно и будет зависеть от значений непрерывного сообщения х(t) Поэтому важно выяснить, как зависят информационные характеристики непрерывного сообщения от присущего ему закона распределения его символов.

Положим, что непрерывное сообщение обладает известной функцией плотности распределения вероятности его символов р(х) (Рис. 1.2).

Рис. 1.2. Функция плотности распределения вероятности p(x) сообщения(х).

Выберем интервал Δx_k. и обозначим середину этого интервала через x_k. Будем рассматривать все символы непрерывного сообщения, попадающие в интервал Δx_k , как k-тый символ дискретного сообщения. Вероятность появления этого символа дискретного сообщения (P_k) будет определяться выражением:

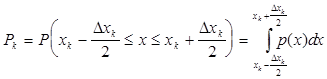
Энтропию полученного таким образом дискретного сообщения (H_Д), на основании формулы Шеннона (1.8), можно записать в виде:

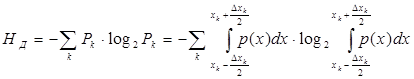(1.14)

Предполагая, что функция p(x) вместе со своей производной непрерывная, имеем:

.

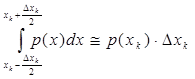Исходное непрерывное сообщение можно рассматривать как предел сформированного дискретного сообщения при Δx_k→0 (т.е. при стремлении объёма алфавита сформированного дискретного сообщения к бесконечности). Поэтому, подставив приведенное выше выражения в (1.14) и перейдя к пределу, получим выражение для энтропии непрерывного сообщения:

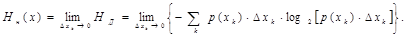
Заменяя в этом выражении логарифм произведения суммой логарифмов сомножителей, преобразуем это выражение к виду

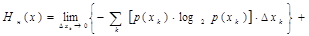
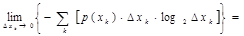
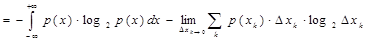(1.15)

Обозначим первое слагаемое в этом выражении как H_x, а второе - как H_Δ. Легко показать, что слагаемое H_Δ обращается в бесконечность при Δx_k→0 независимо от вида функции плотности распределения вероятности символов непрерывного сообщения (р(х)).

Действительно, если принять, что интервалы Δx_k одинаковы, т.е. Δx_k = Δx для всех значений k, то для второго слагаемого в выражении (1.15) имеем:

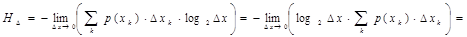
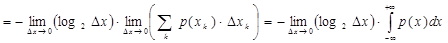
С учетом того, что 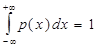, получаем

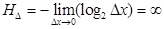
На основании выше изложенного можно сделать следующие выводы:

1. Непрерывные сообщения не имеют абсолютной меры энтропии. Их полная энтропия равна бесконечности.

2. Второе слагаемое в выражении (1.15) стремится к бесконечности одинаковым образом для любых непрерывных сообщений независимо от присущего им закона распределения.

На практике при определении различных информационных характеристик непрерывных сообщений, которое в реальных условиях всегда действует на фоне шума, приходится вычислять разность энтропий сообщения и шума. При этом бесконечно большие слагаемые H_Δ в энтропии сообщения и энтропии шума взаимно уничтожаются, так как они не зависят от законов распределения символов сообщения и шума. И основное значение приобретает первое слагаемое H_x в выражении (1.15).

Таким образом, за меру энтропии непрерывного сообщения можно принять выражение

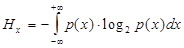. (1.16)

Вычисленную таким образом энтропию называют относительной или дифференциальной, так как она определяет не полную энтропию непрерывного сообщения, равную, как было показано, бесконечности, а только ту ее часть (H_x), которая зависит от закона распределения символов непрерывного сообщения. И под энтропией непрерывного сообщения, как правило, понимают именно дифференциальную энтропию H_x.