Примеры вычисления работы силы

Работа силы в общем случае зависит от характера движения точки приложения силы. Следовательно, для вычисления работы надо знать движение этой точки. Но в природе имеются силы и примеры движения, для которых работу можно вычислить сравнительно просто, зная начальное и конечное положение точки.

Работа силы тяжести.Силу тяжести 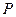материальной точки массой 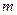вблизи поверхности Земли можно считать постоянной, равной 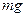, направленной по вертикали вниз. Если взять оси координат 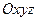, где ось 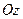направлена по вертикали вверх, то

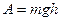, (188)

где 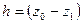– высота опускания точки.

При подъеме точки высота 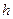является отрицательной. Следовательно, в общем случае работа силы тяжести 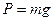равна

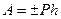. (189)

Если имеем систему 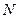материальных точек, то для каждой точки с массой 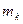будем иметь работу ее силы тяжести

,

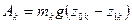где 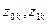– начальная и конечная координаты точки.

Работа всех сил тяжести системы материальных точек

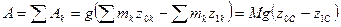, (190)

где 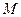– масса системы точек; 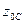и 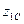– начальная и конечная координаты центра масс системы точек. Вводя обозначение для изменения высоты центра масс 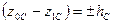, имеем

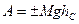. (190')

Работа линейной силы упругости. Линейной силой упругости (или линейной восстанавливающей силой) называют силу, действующую по закону Гука:

,

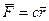где 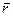– расстояние от точки равновесия, где сила равна нулю, до рассматриваемой точки 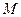; 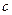– постоянный коэффициент жесткости.

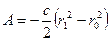. (191)

По этой формуле вычисляют работу линейной силы упругости пружины при перемещении по любому пути из точки 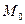, в которой ее удлинение (начальная деформация) равно 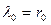, в точку 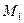, где деформация соответственно равна 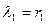. В новых обозначениях (191) принимает вид

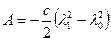. (191')

Работа силы, приложенной к твердому телу. Получим формулы для вычисления элементарной и полной работы силы, приложенной в какой-либо точке твердого тела, которое совершает то или иное движение. Сначала рассмотрим поступательное и вращательное движения тела, а затем общий случай движения твердого тела.

При поступательном движении твердого тела все точки тела имеют одинаковые по модулю и направлению скорости. Следовательно, если сила 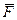приложена к точке 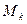, то, так как ,

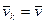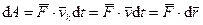, (192)

где 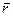– радиус-вектор произвольной точки твердого тела. На каком-либо перемещении полная работа

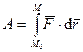. (193)

При вращении твердого тела вокруг неподвижной оси скорость точки 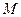можно вычислить по векторной формуле Эйлера:

,

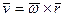тогда элементарную работу силы 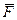определим по формуле

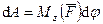. (194)

Таким образом, элементарная работа силы, приложенной к какой-либо точке тела, вращающегося вокруг неподвижной оси, равна произведению момента силы относительно оси вращения на дифференциал угла поворота тела.

Полная работа

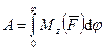. (195)

В частном случае, если момент силы относительно оси вращения является постоянным, т. е. 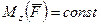, работу определяют по формуле

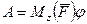. (196)

Используя определение мощности силы

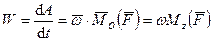. (197)

Мощность силы, приложенной к вращающемуся вокруг неподвижной оси твердому телу, равна произведению угловой скорости тела на момент силы относительно оси вращения тела.

Для свободного тела в общем случае движения скорость точки 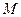, в которой приложена сила ,

,

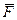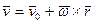следовательно,

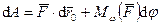. (198)

Таким образом, элементарная работа силы, приложенной в какой-либо точке твердого тела, в общем случае движения складывается из элементарной работы на элементарном поступательном перемещении вместе с какой-либо точкой тела и на элементарном вращательном перемещении вокруг этой точки.

В случае вращения твердого тела вокруг неподвижной точки, выбрав эту точку за полюс , для элементарной работы имеем

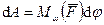. (199)

Поворот на угол 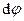следует рассматривать в каждый момент времени вокруг своей мгновенной оси вращения.

Работа внутренних сил твердого тела. Для твердого тела сумма работ внутренних сил равна нулю при любом его перемещении.