Мгновенный центр ускорений
В каждый момент движения плоской фигуры в своей плоскости, если 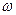 и
и 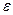 не равны нулю одновременно, имеется единственная точка этой фигуры, ускорение которой равно нулю. Эту точку называют мгновенным центром ускорений. Обозначим ее через
не равны нулю одновременно, имеется единственная точка этой фигуры, ускорение которой равно нулю. Эту точку называют мгновенным центром ускорений. Обозначим ее через 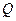 . Пусть
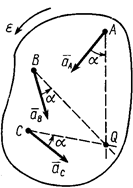
. Пусть 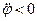 (рис. 39). Мгновенный центр ускорений лежит на линии, проведенной под углом
(рис. 39). Мгновенный центр ускорений лежит на линии, проведенной под углом 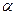 к ускорению точки, тангенс которого вычисляем по формуле:
к ускорению точки, тангенс которого вычисляем по формуле:
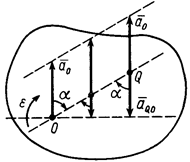
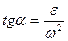 .
.
 При этом угол
При этом угол 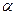 надо отложить от ускорения
надо отложить от ускорения 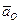 в направлении дуговой стрелки углового ускорения
в направлении дуговой стрелки углового ускорения 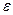 , т.е. в рассматриваемом случае по часовой стрелке. Только в точках этой прямой ускорение
, т.е. в рассматриваемом случае по часовой стрелке. Только в точках этой прямой ускорение 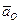 и ускорение от вращения
и ускорение от вращения 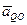 могут иметь противоположные направления и одинаковые значения, т.е.:
могут иметь противоположные направления и одинаковые значения, т.е.:
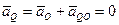 , и тогда
, и тогда
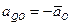 .
.
Но 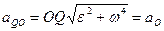 , следовательно,
, следовательно,
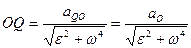 .
.
Мгновенный центр ускорений является единственной точкой плоской фигуры, ускорение которой в рассматриваемый момент времени равно нулю. В другой момент времени мгновенный центр ускорений находится в общем случае в другой точке плоской фигуры.
Если мгновенный центр ускорений известен, то, выбрав его за полюс, для ускорения точки 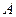 плоской фигуры по формуле (93) получаем
плоской фигуры по формуле (93) получаем
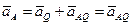 , т.к.
, т.к. 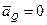 .
.
Следовательно:
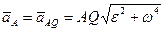 . (99)
. (99)
 Ускорение
Ускорение 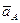 направлено под углом
направлено под углом 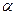 к отрезку
к отрезку 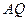 , соединяющему точку
, соединяющему точку 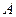 с мгновенным центром ускорений в сторону дуговой стрелки углового ускорения
с мгновенным центром ускорений в сторону дуговой стрелки углового ускорения 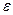 (рис. 40).
(рис. 40).
Для точки 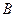 аналогично
аналогично
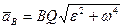 (100)
(100)
и ускорение 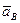 также направлено под углом
также направлено под углом 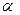 к отрезку
к отрезку 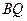
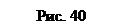 Из формул (99) и (100) имеем
Из формул (99) и (100) имеем
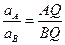 , (101)
, (101)
т.е. ускорения точек плоской фигуры при плоском движении пропорциональны расстояниям от этих точек до мгновенного центра ускорений.
Итак, суммируя результаты, получаем, что ускорения точек плоской фигуры при плоском движении можно определить так же, как и при вращательном движении плоской фигуры вокруг мгновенного центра ускорений с угловой скоростью 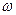 и угловым ускорением
и угловым ускорением 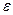 .
.
Для вычисления скоростей точек плоской фигуры при плоском движении принимают, что плоская фигура вращается вокруг мгновенного центра скоростей, а для вычисления ускорения следует считать, что она вращается вокруг мгновенного центра ускорений.
Дата добавления: 2017-01-29; просмотров: 541;
