Скорости и ускорения точек тела при вращении вокруг неподвижной оси
Известно уравнение вращения твердого тела вокруг неподвижной оси  (рис. 29). Расстояние
(рис. 29). Расстояние 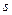 точки
точки 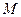 в подвижной плоскости
в подвижной плоскости  по дуге окружности (траектории точки), отсчитываемое от точки
по дуге окружности (траектории точки), отсчитываемое от точки  , расположенной в неподвижной плоскости, выражается через угол
, расположенной в неподвижной плоскости, выражается через угол 
 зависимостью
зависимостью 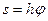 , где
, где 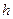 – радиус окружности, по которой
– радиус окружности, по которой 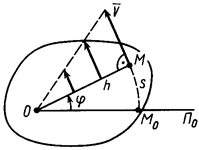 перемещается точка. Он является кратчайшим расстоянием от точки
перемещается точка. Он является кратчайшим расстоянием от точки 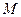 до оси вращения. Его иногда называют радиусом вращения точки. У каждой точки тела радиус вращения остается неизменным при вращении тела вокруг неподвижной оси.
до оси вращения. Его иногда называют радиусом вращения точки. У каждой точки тела радиус вращения остается неизменным при вращении тела вокруг неподвижной оси.
Алгебраическую скорость точки 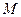 определяем по формуле
определяем по формуле
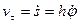
Модуль скорости точки
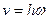 . (70)
. (70)
Скорости точек тела при вращении вокруг неподвижной оси пропорциональны их кратчайшим расстояниям до этой оси. Коэффициентом пропорциональности является угловая скорость. Скорости точек направлены по касательным к траекториям и, следовательно, перпендикулярны радиусам вращения.
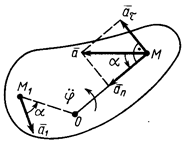
Скорости точек тела, расположенных на отрезке прямой 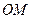 , в соответствии с (70) распределены по линейному закону. Они взаимно параллельны, и их концы располагаются на одной прямой, проходящей через ось вращения Ускорение точки разлагаем на касательную и нормальную составляющие, т. е.
, в соответствии с (70) распределены по линейному закону. Они взаимно параллельны, и их концы располагаются на одной прямой, проходящей через ось вращения Ускорение точки разлагаем на касательную и нормальную составляющие, т. е.
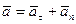 .
.
Касательное и нормальное ускорения вычисляются по формулам:
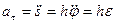 ,
, 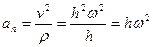 ,
,
так как для окружности радиус кривизны 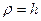 (рис. 30). Таким образом,
(рис. 30). Таким образом,
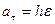 ,
, 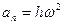 ,
,
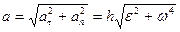 . (71)
. (71)
 Касательные, нормальные и полные ускорения точек, как и скорости, распределены тоже по линейному закону. Они линейно зависят от расстояний точек до оси вращения. Нормальное ускорение направлено по радиусу окружности к оси вращения. Направление касательного ускорения зависит от знака алгебраического углового ускорения. При
Касательные, нормальные и полные ускорения точек, как и скорости, распределены тоже по линейному закону. Они линейно зависят от расстояний точек до оси вращения. Нормальное ускорение направлено по радиусу окружности к оси вращения. Направление касательного ускорения зависит от знака алгебраического углового ускорения. При 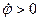 и
и 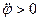 или
или 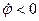 и
и 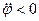 имеем ускоренное вращение тела и направления векторов
имеем ускоренное вращение тела и направления векторов 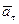 и
и 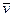 совпадают. Если
совпадают. Если 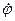 и
и 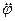 имеют разные знаки (замедленное вращение), то
имеют разные знаки (замедленное вращение), то 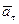 и
и 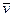 направлены противоположно друг другу.
направлены противоположно друг другу.
Обозначив 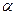 угол между полным ускорением точки и ее радиусом вращения, имеем
угол между полным ускорением точки и ее радиусом вращения, имеем
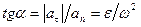 , (72)
, (72)
так как нормальное ускорение 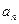 всегда положительно. Угол
всегда положительно. Угол 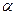 для всех точек тела один и тот же. Откладывать его следует от ускорения к радиусу вращения в направлении дуговой стрелки углового ускорения независимо от направления вращения твердого тела.
для всех точек тела один и тот же. Откладывать его следует от ускорения к радиусу вращения в направлении дуговой стрелки углового ускорения независимо от направления вращения твердого тела.
Дата добавления: 2017-01-29; просмотров: 665;
