Кодирование сигналов
Кодирование сигналов служит для обмена информацией между отдельными составляющими СУ ТОУ (САУ или АСУ) (схемами, узлами, устройствами, блоками), ее обработки и хранение с требуемой точностью и надежностью (самая высокая помехозащищенность). Кодирование состоит в использовании кода – универсального способа отображения информации при ее передаче, обработке и хранении. Код представляет собой систему соответствий между элементами сообщений и сигналами, при помощи которых эти элементы можно зафиксировать. В коде различные виды сигналов одной физической природы называются символами. Конечная совокупность символов, выбранная для передачи конкретного сообщения, называется словом. Кодовый сигнал (код) - особый вид сигналов (цифровой сигнал). Кодирование может производиться либо от аналоговых, либо от дискретных сигналов (рис.1.2).
пример: 0 или 1 – символы в одном разряде двоичного кода (1 бит информации);
байт содержит 8 бит информации (8 разрядов), т.е. например, 10001001 байтовое слово.
В АСУ так же как в любых информационно-измерительных системах (ИИС) применяются два способа передачи сообщений (совокупности слов): параллельным кодом – все символы одного слова передаются одновременно по каналам, число которых соответствует количеству символов, т.е. длине слова (для передачи байтового слова нужно 8 каналов); последовательным кодом - символы одного слова передаются друг за другом по одному каналу.
Выбор кодов определяется спецификой восприятия и преобразования информации, характерной для данного уровня АСУ ТП и ее составляющих.
Основными требованиями, которые выдвигаются при выборе способа кодирования, являются: экономичность отображения информации, простота технической реализации устройств кодирования, удобство выполнения вычислительных операций и надежность передачи сообщений.
Для выполнения этих требований, особенно связанных с удобством выполнения вычислительных операций, наиболее пригоден цифровой код (алфавит), число символов в котором зависит от основания системы счисления и обычно не превышает 10 или 16. Такой подход позволяет осуществлять кодирование не только чисел, но и понятий.
При помощи кода с основанием n любое число можно представить в виде:
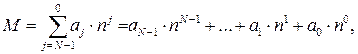 (1.1)
(1.1)
где N – количество разрядов; aj – количество символов в одном разряде.
Если опустить nj , то получим более компактную запись N – разрядного (от N –1 до 0) числа М:
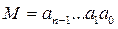 . (1.2)
. (1.2)
Пример:М = 123 = 1×103-1 + 2 × 102-1+ 3 ×10° (n=10).
Из формул (1.1) и (1.2) следует, что одно и то же число М в зависимости от основания n при кодировании формируется из разного количества символов в одном разряде (aj)и количества разрядов (N). Например, цифровой 3-разрядный десятичный вольтметр, представляющий информацию в коде с основанием 10, имеет в каждом разряде 10 различных цифр (символов), может с точностью до 1 младшего разряда выдать 1000 (0, 1, …, 999) различных значений измеряемого параметра (напряжения). для осуществления той же операции в двоичном коде (коде с основанием 2) потребуется 10 разрядов с двумя значащими цифрами в каждом из них (210 = 1024).
Пусть n – максимальное число символов в разряде (основание кода), а N – число разрядов.
Тогда возможное количество различных сообщений составляет
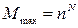 . (1.3)
. (1.3)
Например, 1024 = 210; в двоичном коде с помощью 10 разрядов можно записать максимальное число 1024, т.е. для передачи числа 1024 понадобится 10 каналов (разрядов) двоичного кода.
Экономичность кодирования будет тем выше, чем меньше знаков следует затратить на передачу одного и того же сообщения. При передаче сообщений по каналу связи количество знаков определяет также и необходимое для этого время.
По соображениям простоты технической реализации явное преимущество на стороне кода с n = 2, при котором для хранения, передачи и обработки информации необходимы дискретные элементы с двумя устойчивыми состояниями.
Пример: логические функции: «да» - «нет», состояние блока ТОУ: «включено» - «отключено», действие (операция): «выполнено» – «не выполнено», техническое состояние узла ТОУ: «исправен» - «неисправен», кодируется цифрами «1» - «0».
Поэтому двоичный код получил широкое распространение в цифровых устройствах измерения контроля, управления и автоматизации.
При вводе двоично-кодированной информации в ЭВМ для компактной записи часто используют коды, основание которых являются целой степенью чисел 2:23 = 8 (восьмеричный) и 24 = 16 (шестнадцатеричный).
Для примера рассмотрим формирование чисел в различных системах счисления (табл.1.1).
Таблица 1.1
| Система счисления | |||
| Десятичная n = 10 | Двоичная n = 2 | Восьмеричная n = 8 | Шестнадцатеричная n = 16 |
| А | |||
| 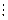
| 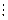
| В…F |
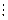
| 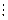
| 
| 
|
Рассмотрим двоичные позиционные коды. Среди них широко используются специальные коды: прямой, обратный, дополнительный. Во всех этих кодах введен специальный знаковый разряд.
В прямом коде знак кодируется 0 для положительных и 1 – для отрицательных чисел. Пример 1100 (+12) в прямом коде 0.1100. Прямой код удобен для выполнения операций умножения, т.к. знак произведения получается автоматически. Однако затруднено вычитание. Этот недостаток устраняется применением обратного и дополнительного кодов, отличающихся от прямого способом представления отрицательных чисел. Обратный код отрицательного числа образуется инвертированием всех значащих разрядов (-1100 (– 12) в обратном коде: 1.0011). В дополнительном коде после инвертирования разрядов в младший размер добавляется 1. Пример: - 1100 в дополнительном коде: 1.0100.
В системах и устройствах отображение информации (цифровой индикации) нашли применение двоично-десятичные коды. В этих кодах каждая десятичная цифра представляется четырьмя двоичными (тетрадой).
Системы кодирования в 2-10 кодах показаны в табл.1.2.
Таблица 1.2
| Код | Десятичные числа | Использование | |||||||||
| В системах ЧПУ станков | |||||||||||
| 2 и 5 | Для контроля и коррекции информации | ||||||||||
| Код Грея | Для повышения надежности в АЦП и кодовых датчиках |
Выбор частоты квантования для аналого-цифрового преобразователя (АЦП). При квантовании и последующем кодировании сигналов, например в случае квантования по времени в виде импульсов, модулированных по амплитуде (рис.1.3, б), дальнейшее преобразование сигналов в АЦП заключается в представлении амплитуды импульсов двоичным кодом. При этом установление частоты квантования усложняется в тех случаях, когда исходный аналоговый сигнал y(f) является произвольной функцией времени и не поддается аналитическому выражению. Тогда частота квантования определяется на основании теоремы В.А.Котельникова. В этой теореме рассматривается непрерывная функция, имеющая ограниченный спектр частот, т.е. содержит частоты от 0 до fmаx. Такую функцию можно представить с достаточной точностью при помощи чисел, следующих друг за другом через интервалы времени
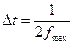 . (1.4)
. (1.4)
Следовательно, исходя из формулы (1.4), определяющей шаг квантования, при частоте квантования
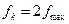 (1.5)
(1.5)
функция, содержащая ограниченный спектр частот воспроизводится достаточно точно.
Дата добавления: 2017-01-13; просмотров: 1215;
