Методика сортоиспытания

В настоящее время сортоиспытание лесных древесных пород проводится по утвержденным в установленном порядке методикам. При этом при закладке опытов следует предварительно произвести их планирование, чтобы определить необходимое количество пун­ктов сортоиспытания, объем выборки, количество повторений и схему размещения сортов в предполагаемых опытах.

Эти показатели будут зависеть от многих факторов, среди кото­рых главными являются следующие:

• количество пунктов сортоиспытания — от этого зависит реп­резентативность и объективность оценки сорта;

• оцениваемые параметры сортов и их вариации (например, диаметры значительно вариабельнее высот, запасы насаждений на единицу площади отличаются большей стабильностью);

• генетическое разнообразие испытуемых сортов (в зависимос­ти от того, являются ли они сортами-клонами или сортами-попу­ляциями, коэффициенты варьирования тех или иных оцениваемых показателей будут значительно меняться в сторону увеличения у последних);

• длительность срока испытания (в краткосрочных опытах мож­но ограничиваться меньшим числом и более густым размещением деревьев, чем в длительных);

целевое назначение сортов (для высокоинтенсивных планта­ций сорта должны обладать большей выравненностью, чем для на­саждений с обычной агротехникой выращивания (лесные культуры, защитные насаждения и т.п.), где допускается выравнивание полога при рубках ухода);

• заданный размер превышения испытуемого сорта над конт­ролем (зависит как от требований производства, так и от возмож­ностей исходного материала).

Планирование размера выборки. Следует иметь в виду, что неко­торые отечественные методики сортоиспытания, в частности то­полей (С. А. Ростовцев, 1961; Н. В. Старова, 1962; Г. П. Озолин, 1970), рекомендуют соответственно 144, 100, 130 растений на де­лянку. В Чехословакии сортоиспытание тополя проводилось в по-пулетумах при четырехкратной повторности по четыре растения в каждой повторности (Г. П. Озолин, 1970). Другие лесные породы рекомендуется высаживать по 100-150 растений на делянку. Шрек (цит. по Э. Ромедеру, Г. Шенбаху, 1962) нашел, что при испыта­нии потомства сосны достаточно семи растений, чтобы получить статистически достоверный результат при изучении энергии рос­та. Однако, учитывая возможный отпад, Шрек рекомендует вво­дить на делянку девять растений. Э. Ромедер и Г. Шенбах (1962) считают, что «весьма точную среднюю величину можно получить лишь при наличии 20-40 индивидуумов». Такое разнообразие ре­комендаций ставит в затруднительное положение исследователя, планирующего новый эксперимент по сортоиспытанию лесных пород.

А.П. Царев (1985) попытался найти объективные подходы при решении этого вопроса, основываясь на существующих положени­ях математической статистики. При этом было выделено два прин­ципиальных этапа сортоиспытания: 1) много испытываемых вари­антов (сортов) при небольшой представленности каждого; 2) мало испытываемых вариантов (сортов) при значительной представлен­ности каждого.

Первый этап характерен для конкурсного испытания, второй — для производственного.

На первом этапе селекционер стремится включить в испытание как можно большее количество форм, гибридов, клонов, сортов, чтобы не упустить перспективный сорт и иметь гарантию результа­тов своего труда. Но ввиду большого количества вариантов (сортов) невозможно каждый из них повторить множество раз, так как это потребовало бы больших площадей и трудозатрат и не всегда при-водило бы к нужному результату. Однако количество экземпляров каждого сорта должно быть достаточным для получения объектив­ного суждения. Поэтому требуется определить наименьший, но до-статочный размер выборки для одного варианта, который давал бы объективные результаты при изучении такого варьирующего пока­зателя как рост.

Для определения размера выборки в статистической литературе (Дж. У. Снедекор, 1961) предлагаются методы, учитывающие неко­торую заранее заданную величину

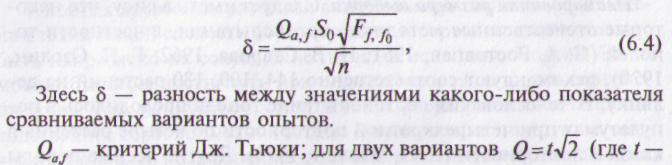
показатель достоверности), если вариантов более двух, то значение Q берется из таблиц, помещенных, например, в книге Дж. У. Сне-декора (1961). В таблицах приведено значение Q в зависимости от числа вариантов а планируемого опыта и числа степеней свободы f в нем.

S₀ — заранее заданная оценка среднеквадратичного отклонения при числе степеней свободы f₀ у пробного предварительного опыта; f₀ может быть также определено по таблицам (Дж. У. Снедекор).

Ff,f₀ — критерий Р. Фишера для определенной вероятности Р и числа степеней свободы, равного f и f₀. Для большей уверенности, что прогноз будет правильным, рекомендуется выбрать Р= 0,75. Это означает, что в трех случаях из четырех найденная величина 5 соот­ветствует действительности; Ff,f₀ берется из таблиц при f₁ =f и f₂= f₀.

п — число наблюдений в одном варианте опыта.

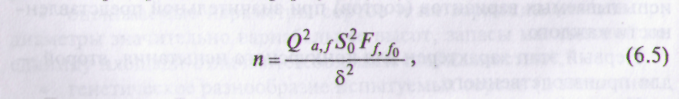Необходимое число наблюдений в одном варианте опыта опре­деляют преобразованием формулы (6.4):

как Q и F зависят от и, то для решения данного уравнения используется метод последовательного приближения. При этом для начала берется явно завышенное значение п.

Применение этого метода рассмотрим на примере. Допустим, требуется определить количество деревьев в одном варианте при испытании двух сортов из секции настоящих тополей. Предвари­тельные выводы о росте тополей этой секции можно сделать при пятилетнем возрасте тополей. Положим, ставится задача выявить разницу в росте, которая составляет 10% высоты исследуемых рас­тений. Высота пятилетних тополей в Центральной России может достигать 5 м. Следовательно, искомая разница 5 = 0,5 м. Чтобы воспользоваться формулой (6.5), определим ее составляющие.

Значение Q_af берется из таблиц при а = 2, f принимается по явно завышенному п. Допустим, явно завышенное п = 121, тогда f = = а(n-1) = 2 х 120 = 240. И искомое Q_2,240= 2,77.

Значение S₀ берется из предварительных опытов или рассчиты­вается с учетом коэффициентов вариации. Как показали исследо­вания А. В. Тюрина (1961) и О. А. Трулля (1966), коэффициенты вариации высот у взрослых деревьев колеблются от 8 до 13 %. Сле­довательно, верхний g и нижний h пределы среднеквадратичного отклонения у исследуемого материала будут равны соответственно 0,65 и 0,40 м, т.е. S₀ = (0,40 +0,65)/2 = 0,53 м.

Значение S₀ можно получить из таблицы (Дж. У. Снедекор, 1961). В данном случае g/h = 0,65:0,40 = 1,63; f₀ = 4; Ff_0,f = F_,240.4 = 2,08.

Подставив полученные данные в формулу (6.5), найдем первое приближение:

Так как вычисленное значение 5 больше заданного (5 = 0,5), то, увеличив первое приближение на 1, при п = 19 получим Q_2,36 = 2,87, F_36.4 = 2,084; при этом 5 = 0,507, что также больше заданного. Уве­личив л еще на 1, при п = 20 находим, что Q_2,38 = 2,86 и F_38.4 = 2,08; при этом 8 = 0,492. Эта величина меньше заданной. Следовательно, приемлемое значение выборки при сравнении двух сортов может составить 19-20 экземпляров на вариант. При большем количестве сравниваемых сортов размер выборки увеличивается, с увеличени­ем δ — уменьшается. Для упрощения вычислений в качестве при­мера составлена табл. 6.3.

Как видно из данных таблицы, принятый ранее вывод об увели­чении числа наблюдений с уменьшением значения заданной раз­ницы подтверждается. С увеличением числа вариантов количество наблюдений также увеличивается. При δ > 50% средний планируе­мый размер выборки стабилизируется. При числе наблюдений менее двух формулы (6.4) и (6.5) не применимы, поскольку число сте­пеней свободы становится менее единицы.

Таблица 6.3

Планируемый размер выборки в зависимости

от количества вариантов и значения заданной разницы 5

между сравниваемыми вариантами при сортоиспытании