Основные статистические характеристики экспериментальных данных

Основные статистические характеристики делят на две основные группы: меры центральной тенденции и характеристики вариации.

Центральную тенденцию выборки позволяют оценить такие статистические характеристики, как среднее арифметическое значение, мода, медиана.

Наиболее просто получаемой мерой центральной тенденции является мода. Мода (Мо) – это такое значение в множестве наблюдений, которое встречается наиболее часто. В совокупности значений (2, 6, 6, 8, 7, 33, 9, 9, 9, 10) модой является 9, потому что оно встречается чаще любого другого значения. В случае, когда все значения в группе встречаются одинаково часто, считают, что эта группа не имеет моды.

Когда два соседних значения в ранжированном ряду имеют одинаковую частоту и они больше частоты любого другого значения, мода есть среднее этих двух значений.

Если два несмежных значения в группе имеют равные частоты, и они больше частот любого значения, то существуют две моды (например, в совокупности значений 10, 11, 11, 11, 12, 13, 14, 14, 14, 17 модами являются 11 и 14); в таком случае группа измерений или оценок является бимодальной.

Наибольшей модой в группе называется единственное значение, которое удовлетворяет определению моды. Однако во всей группе может быть несколько меньших мод. Эти меньшие моды представляют собой локальные вершины распределения частот.

Медиана (Me) – середина ранжированного ряда результатов измерений. Если данные содержат четное число различных значений, то медиана есть точка, лежащая посередине между двумя центральными значениями, когда они упорядочены.

Среднее арифметическое значение 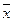для неупорядоченного ряда измерений вычисляют по формуле:

,

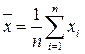где 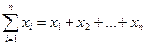. Например, для данных 4,1; 4,4; 4,5; 4,7; 4,8 вычислим :

.

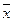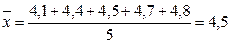Каждая из выше вычисленных мер центра является наиболее пригодной для использования в определенных условиях.

Мода вычисляется наиболее просто – ее можно определить на глаз. Более того, для очень больших групп данных это достаточно стабильная мера центра распределения.

Медиана занимает промежуточное положение между модой и средним с точки зрения ее вычисления. Эта мера получается особенно легко в случае ранжированных данных.

Среднее множество данных предполагает в основном арифметические операции.

На величину среднего влияют значения всех результатов. Медиана и мода не требуют для определения всех значений. Посмотрим, что произойдет со средним, медианой и модой, когда удвоится максимальное значение в следующем множестве:

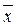Me Мо

Множество 1: 1, 3, 3, 5, 6, 7, 8 33/7 5 3

Множество 2: 1, 3, 3, 5, 6, 7, 16 41/7 5 3

На величину среднего особенно влияют результаты, которые называют “выбросами”, т.е. данные, находящиеся далеко от центра группы оценок.

Вычисление моды, медианы или среднего – чисто техническая процедура. Однако выбор из этих трех мер и их интерпретация зачастую требуют определенного размышления. В процессе выбора следует установить следующее:

– в малых группах мода может быть совершенно нестабильной. Например, мода группы: 1, 1, 1, 3, 5, 7, 7, 8 равна 1; но если одна из единиц превратится в нуль, а другая – в два, то мода будет равна 7;

– на медиану не влияют величины “больших” и “малых” значений. Например, в группе из 50 значений медиана не изменится, если наибольшее значение утроится;

– на величину среднего влияет каждое значение. Если одно какое-нибудь значение меняется на c единиц, 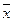изменится в том же направлении на c/n единиц;

– некоторые множества данных не имеют центральной тенденции, что часто вводит в заблуждение при вычислении только одной меры центральной тенденции. Особенно это справедливо для групп, имеющих более чем одну моду;

– когда считают, что группа данных является выборкой из большой симметричной группы, среднее выборки, вероятно, ближе к центру большой группы, чем медиана и мода.

Все средние характеристики дают общую характеристику ряда результатов измерений. На практике нас часто интересует, как сильно каждый результат отклоняется от среднего значения. Однако легко можно представить, что две группы результатов измерений имеют одинаковые средние, но различные значения измерений. Например, для ряда 3, 6, 3 – среднее значение 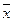= 4; для ряда 5, 2, 5 – также среднее значение 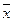= 4, несмотря на существенное различие этих рядов.

Поэтому средние характеристики всегда необходимо дополнять показателями вариации, или колеблемости.

К характеристикам вариации, или колеблемости, результатов измерений относят размах варьирования, дисперсию, среднее квадратическое отклонение, коэффициент вариации, стандартную ошибку средней арифметической.

Самой простой характеристикой вариации является размах варьирования. Его определяют как разность между наибольшим и наименьшим результатами измерений. Однако он улавливает только крайние отклонения, но не отражает отклонений всех результатов.

Чтобы дать обобщающую характеристику, можно вычислить отклонения от среднего результата. Например, для ряда 3, 6, 3 значения 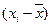будут следующими: 3 – 4 = – 1; 6 – 4 = 2; 3 – 4 = – 1. Сумма этих отклонений (– 1) + 2 + (– 1) всегда равна 0. Чтобы избежать этого, значения каждого отклонения возводят в квадрат: (– 1)² + 2² + (– 1)² = 6.

Значение 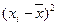делает отклонения от средней более явственными: малые отклонения становятся еще меньше (0,5²=0,25), а большие – еще больше (5² = 25). Получившуюся сумму 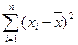называют суммой квадратов отклонений. Разделив эту сумму на число измерений, получают средний квадрат отклонений, или дисперсию. Она обозначается s² и вычисляется по формуле:

.

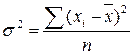Если число измерений не более 30, т.е. n ≤ 30, используется формула:

.

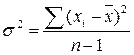Величина n – 1 = k называется числом степеней свободы, под которым подразумевается число свободно варьирующих членов совокупности. Установлено, что при вычислении показателей вариации один член эмпирической совокупности всегда не имеет степени свободы.

Эти формулы применяются, когда результаты представлены неупорядоченной (обычной) выборкой.

Из характеристик колеблемости наиболее часто используется среднее квадратическое отклонение, которое определяется как положительное значение корня квадратного из значения дисперсии, т.е.:

.

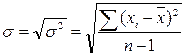Среднее квадратическое отклонение или стандартное отклонение характеризует степень отклонения результатов от среднего значения в абсолютных единицах и имеет те же единицы измерения, что и результаты измерения.

Однако для сравнения колеблемости двух и более совокупностей, имеющих различные единицы измерения, эта характеристика не пригодна.

Коэффициент вариации определяется как отношение среднего квадратического отклонения к среднему арифметическому, выраженное в процентах. Вычисляется он по формуле:

.

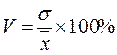В спортивной практике колеблемость результатов измерений в зависимости от величины коэффициента вариации считают небольшой
(0 – 10 %), средней (11 – 20 %) и большой (V > 20 %).

Коэффициент вариации имеет большое значение в статистической обработке результатов измерений, т. к., будучи величиной относительной (измеряется в процентах), позволяет сравнивать между собой колеблемость результатов измерений, имеющих различные единицы измерения. Коэффициент вариации можно использовать лишь в том случае, если измерения выполнены в шкале отношений.

2.4.2. Анализ статистических данных в MS Excel. Инструменты анализа: описательная статистика, корреляция.

В состав электронных таблиц Microsoft Excel входит так называемый пакет анализа – набор инструментов, предназначенный для решения сложных статистических задач. Данный пакет производит анализ статистических данных с помощью макрофункций и позволяет, выполнив одно действие, получить на выходе большое количество результатов. В пакете анализа, имеющемся в Excel, среди прочих инструментов анализа имеется разделы «Описательная статистика» и «Корреляция».

Инструмент «Описательная статистика» позволяет нам получить значительный перечень рассчитанных статистических характеристик для большого количества числовых рядов. С помощью инструмента «Корреляция» мы получаем корреляционную матрицу, содержащую все возможные парные коэффициенты корреляции. Для k рядов будет получено k (k – 1)/2 коэффициентов корреляции.

Пакет анализа вызывается с помощью пункта меню Сервис – Анализ данных… Если этот пункт меню отсутствует, значит, пакет анализа не установлен. Для его установки надо вызвать пункт меню Сервис – Надстройки… и включить надстройку «Пакет анализа», ОК (см. рисунок 1).

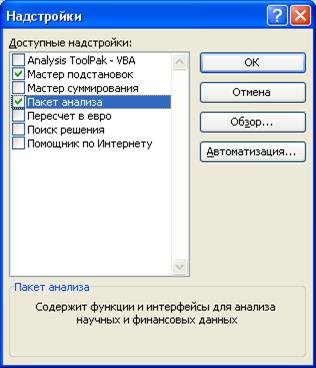
Рисунок 1. Диалоговое окно включения/выключения надстроек

После включения надстройки «Пакет анализа» будет доступен пункт меню Сервис – Анализ данных… При его выборе появляется следующее диалоговое окно (рисунок 2).

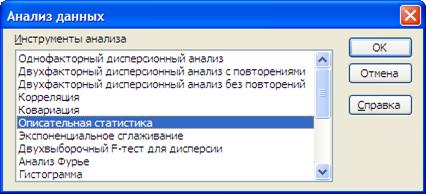
Рисунок 2. Диалоговое окно выбора инструмента для анализа данных

После выбора инструмента «Описательная статистика» и нажатия ОК появится еще одно диалоговое окно (рисунок 3), требующее ввода входных данных и места вывода результатов. Здесь достаточно в поле «Входной интервал» ввести диапазон ячеек, содержащих исходные данные. Можно указать диапазон с заголовками столбцов, в этом случае потребуется включить флажок «Метки в первой строке». Для указания выходного интервала достаточно указать только левую верхнюю ячейку диапазона. Результаты вычисления автоматически займут требуемое количество строк и столбцов в таблице.

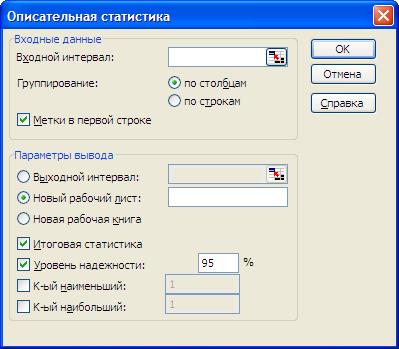
Рисунок 3. Диалоговое окно инструмента «Описательная статистика»

Рассмотрим работу инструмента анализа «Описательная статистика» на следующем примере. В процессе обследования группы школьников (n = 21) измерялись следующие показатели: рост, масса тела, динамометрия правой и левой руки, жизненная емкость легких, проба Штанге и проба Генчи. Результаты были занесены в таблицу (рисунок 4).

Для получения статистических характеристик воспользуемся пакетом анализа, инструментом «Описательная статистика». В поле «Входной интервал» занесем диапазон ячеек В1:Н22. Так как выделенный входной интервал содержит заголовки столбцов, включаем флажок «Метки в первой строке». Для удобства работы в качестве места выхода результата выбираем «Новый рабочий лист». В качестве выводимых данных отметим флажками «Итоговая статистика» и «Уровень надежности: 95 %». Последний флажок позволит вывести параметры доверительного интервала с доверительной вероятностью 0,95. Полученный результат после небольшого форматирования будет выглядеть так, как показано на рисунке 5.

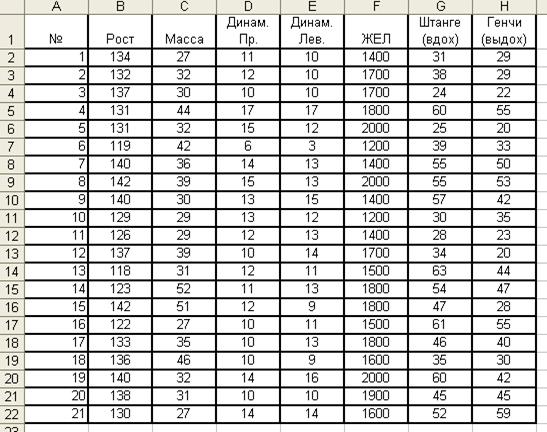
Рисунок 4. Результаты обследования группы школьников

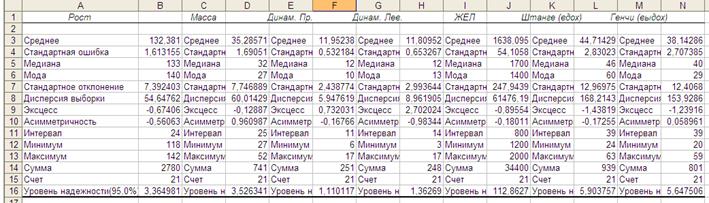
Рисунок 5. Результат работы инструмента «Описательная статистика»

После выбора инструмента «Корреляция» и нажатия ОК в диалоговом окне «Анализ данных» (рисунки 2, 6) появится еще одно диалоговое окно (рисунок 7), требующее ввода входных данных и места вывода результатов. Здесь достаточно в поле «Входной интервал» ввести диапазон ячеек, содержащих исходные данные. Можно указать диапазон с заголовками столбцов, в этом случае потребуется включить флажок «Метки в первой строке». Для указания выходного интервала достаточо указать только левую верхнюю ячейку диапазона. Результаты вычисления автоматически займут требуемое количество строк и столбцов в таблице.

Рисунок 6. Диалоговое окно выбора инструмента для анализа данных

Рисунок 7. Диалоговое окно инструмента «Корреляция»

Рассмотрим работу инструмента анализа «Корреляция» на примере, представленном на рисунке 4.

Для получения корреляционной матрицы воспользуемся пакетом анализа, инструментом «Корреляция». В поле «Входной интервал» занесем диапазон ячеек В1:Н22. Так как выделенный входной интервал содержит заголовки столбцов, включаем флажок «Метки в первой строке». Для удобства работы в качестве места выхода результата выбираем «Новый рабочий лист». Полученный результат после небольшого форматирования будет выглядеть так, как показано на рисунке 8.

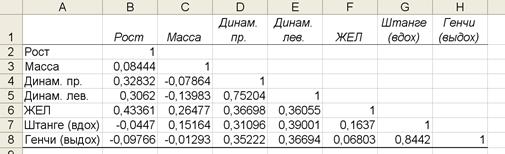
Рисунок 8. Корреляционная матрица

Таким образом, путем выполнения несложных операций мы получаем большое количество результатов вычислений. Стоит отметить, что хотя информационные технологии открывают перед исследователем возможности получения огромного количества информации для анализа, отбор наиболее информативных результатов, окончательная интерпретация и формулировка выводов – работа самого исследователя.

Основные понятия корреляционного анализа экспериментальных данных. Оценка коэффициента корреляции по экспериментальным данным.

В спортивных исследованиях между изучаемыми показателями часто обнаруживается взаимосвязь. Вид ее бывает различным. Например, определение ускорения по известным данным скорости, второй закон Ньютона и другие характеризуют так называемую функциональную зависимость, или взаимосвязь, при которой каждому значению одного показателя соответствует строго определенное значение другого.

К другому виду взаимосвязи относят, например, зависимость веса от длины тела. Одному значению длины тела может соответствовать несколько значений веса и наоборот. В таких случаях, когда одному значению одного показателя соответствует несколько значений другого, взаимосвязь называют статистической.

Изучению статистической взаимосвязи между различными показателями в спортивных исследованиях уделяют большое внимание, поскольку это позволяет вскрыть некоторые закономерности и в дальнейшем описать их как словесно, так и математически с целью использования в практической работе тренера и педагога.

Среди статистических взаимосвязей наиболее важны корреляционные. Корреляция – это статистическая зависимость между случайными величинами, при которой изменение одной из случайных величин приводит к изменению математического ожидания (среднего значения) другой. Например, толкание ядра 3 кг и 5 кг. Улучшение результатов толкания ядра 3 кг вызывает улучшение (в среднем) результата в толкании ядра весом 5 кг.

Статистический метод, который используется для исследования взаимосвязей, называется корреляционным анализом. Основной задачей его является определение формы, тесноты и направленности взаимосвязи изучаемых показателей. Корреляционный анализ позволяет исследовать только статистическую взаимосвязь. Он широко используется в теории тестов для оценки их надежности и информативности. Различные шкалы измерений требуют разных вариантов корреляционного анализа.

Величина коэффициента взаимосвязи рассчитывается с учетом шкалы, использованной для измерений.

Для оценки взаимосвязи, когда измерения производят в шкале отношений или интервалов и форма взаимосвязи линейная, используется коэффициент корреляции Бравэ-Пирсона (коэффициенты корреляции для других шкал измерения в данном пособии не рассматриваются). Обозначается он латинской буквой – r. Вычисление значения r чаще всего производят по формуле:

,

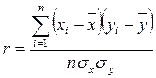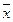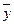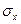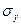где и – средние арифметические значения показателей x и y, и – средние квадратические отклонения, n – число измерений (испытуемых).

В некоторых случаях тесноту взаимосвязи определяют на основании коэффициента детерминации D, который вычисляется по формуле:

.

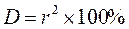Этот коэффициент определяет часть общей вариации одного показателя, которая объясняется вариацией другого показателя. Например, коэффициент корреляции r = –0,677 (между результатами в беге на 30 м с ходу и тройном прыжке с места). Коэффициент детерминации равен:

.

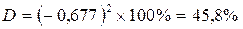Следовательно, 45,8 % рассеяния спортивного результата в тройном прыжке объясняется изменением результатов в беге на 30 м. Иными словами, на оба исследуемых признака действуют общие факторы, вызывающие варьирование этих признаков, и доля общих факторов составляет 45,8%. Остальные 100% – 45,8% = 54,2% приходятся на долю факторов, действующих на исследуемые признаки избирательно.

Оценить статистическую достоверность коэффициента корреляции – это значит определить, существует или нет линейная корреляционная связь между генеральными совокупностями или, что то же, установить, существенно или несущественно отличается от нуля коэффициент корреляции между выборками. Эта задача может быть решена с помощью таблиц критических точек распределения коэффициента корреляции в следующем порядке:

1. Выдвигаются статистические гипотезы. Гипотеза Н₀ предполагает отсутствие статистически значимой взаимосвязи между исследуемыми показателями (r_ген=0). Гипотеза Н₁ предполагает, что существует статистически достоверная взаимосвязь между показателями (r_ген>0).

2. Рассчитывается наблюдаемое значение коэффициента корреляции r_набл.

3. Находится по таблице критическое значение коэффициента корреляции r_крит в зависимости от объема выборки n, уровня значимости a и вида критической области (односторонняя или двусторонняя).

3. Сравнивается r_набл и r_крит.

Если r_набл < r_крит – статистически недостоверным (незначимым). Принимается гипотеза Н₀ Если r_набл ≥ r_крит, коэффициент корреляции считается статистически достоверным (значимым). Принимается гипотеза Н₁.