Многомерные и самонастраивающиеся системы.

Классификация САУ по различным признакам.

Линейные непрерывные и дискретные САУ.

Многомерные и самонастраивающиеся системы.

1.5 Задачи теории, анализа и синтеза линейных систем автоматического управления и регулирования.

Особенностью, усложняющей расчет динамики системы, является то, что в замкнутой системе все физические величины, представляющие воздействие одного звена на другое, связаны в единую замкнутую цепь. Поэтому приходится уравнения динамики всех звеньев системы решать совместно, т.е. иметь дело с дифференциальными уравнениями высокого порядка. Это положение существенно для анализа и синтеза автоматических систем, для исследования устойчивости и качества процессов управления. С этим связан целый арсенал математических методов расчета.

Исторически, первыми автоматическими регуляторами с замкнутым циклом были: регулятор уровня в котле паровой машины И.И.Ползунова (1765 г.) и регулятор скорости вала паровой машины Дж. Уатта (1784 г.). Первые исследования динамики замкнутых автоматических систем, устойчивости и качества процессов регулирования принадлежат И.А. Вышнеградскому (1876 г.).

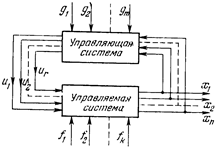
Рис. 6

Выше приводились примеры и схемы автоматических систем с одной задаваемой g(t) и одной регулируемой х величинами. В общем же случае система может иметь много входов и выходов (рис. 6). Это многомерные (или многосвязные) системы.

Передача воздействий в системе представляет передачу потоков информации о состоянии отдельных элементов системы.

Кроме чисто технических автоматических систем аналогичные принципы действия заложены и в биологических системах, экономических системах и т.п., что изучается соответствующими направлениями кибернетики и общей теории систем управления, а также специальными дисциплинами.

Кроме полностью автоматических систем имеются автоматизированные системы управления или полуавтоматические, в которых кроме технических средств в состав системы управления входят люди. Таковы, например, многие автоматизированные системы управления производственными процессами. В простейших случаях в систему управления включается один человек-оператор, например, при полуавтоматическом управлении летательным аппаратом или какой-либо наземной установкой. Таковы и системы дистанционного управления манипуляторами в агрессивных средах.

Все системы автоматического управления и регулирования делятся по различным признакам на следующие основные классы.

1. По основным видам уравнений динамики процессов управления:

а) линейные системы;

б) нелинейные системы.

2. Каждый из этих основных классов делится на:

а) системы с постоянными параметрами (уравнения с постоянными коэффициентами);

б) системы с переменными параметрами (уравнения с переменными коэффициентами);

в) системы с распределенными параметрами (уравнения в частных производных);

г) системы с запаздыванием (уравнения с запаздывающим аргументом).

3. По характеру передачи сигналов различают:

а) непрерывные системы;

б) дискретные системы (импульсные и цифровые);

в) релейные системы.

4. По характеру процессов управления:

а) детерминированные системы (определенные параметры и процессы);

б) стохастические системы (случайные параметры и процессы).

5. По характеру функционирования:

а) обычные системы;

б) адаптивные системы (самонастраивающиеся, самоорганизующиеся, экстремальные);

в) терминальные системы.

Последние отличаются тем, что в них ставится задача достижения определенного состояния системы в конечный момент времени. До этого весь процесс управления может идти достаточно произвольно с оптимизацией по каким-либо другим показателям, например по расходу энергии.

Приведенные выше примеры относятся к обычным системам. Адаптивные системы имеют, как правило, дополнительные блоки и контуры для анализа показателей качества процесса или внешних условий, по которым необходима адаптация системы.

Каждый из этих основных классов систем в свою очередь делится по ряду принципиальных признаков на различные типы и разновидности, не говоря уже о большом разнообразии конструктивного оформления и различной физической природе реальных систем.

Задачами линейной теории автоматического управления и регулирования являются:

1) изучение динамических свойств и характеристик различных типов звеньев автоматических систем любой физической природы и конструкции;

2) формирование функциональных и структурных схем автоматического управления и регулирования;

3) построение динамических характеристик этих систем;

4) определение ошибок и показателей точности замкнутых систем;

5) исследование устойчивости замкнутых систем;

6) оценка качественных показателей процессов управления;

7) определение чувствительности систем к изменению параметров и других факторов;

8) изучение различных видов корректирующих устройств, вводимых в системы для повышения точности и улучшения динамических качеств;

9) создание частотных, корневых и других методов синтеза корректирующих устройств и различных методов оптимизации систем по показателям качества;

10) разработка методов анализа и синтеза сложных многомерных и комбинированных систем автоматического управления.

Все это является базой для грамотного построения замкнутых автоматических систем и для инженерных расчетов при анализе существующих и проектировании новых систем автоматического управления. Эти методы широко применяются не только для систем регулирования и управления как таковых, но и во всех случаях анализа и разработки замкнутых динамических контуров в любых технических системах, в биотехнических и в экономических системах.

Задачи и методы исследования САР.

В теории автоматического регулирования приходится сталкиваться с двумя задачами:

1) исследовать имеющуюся систему автоматического регулирования и определить степень, в какой она удовлетворяет предъявляемым к ней требованиям (анализ системы);

2) по имеющимся требованиям спроектировать систему, удовлетворяющую этим требованиям (синтез системы).

В настоящее время методы анализа и синтеза систем разработаны не с одинаковой полнотой. Наиболее полно разработаны методы анализа линейных систем автоматического регулирования, переходные процессы которых описываются линейными дифференциальными уравнениями различных порядков. Эти методы дают возможность выяснить не только характер, но и количественную сторону переходных процессов. С помощью развивающихся методов анализа нелинейных систем не всегда еще можно получить ответы в том виде, который необходим в инженерной практике.

Применение электронных вычислительных машин расширило возможности исследования нелинейных систем путем моделирования или численного решения нелинейных уравнений, описывающих эти системы, однако значение общей теории этим обстоятельством не снижается. Методы синтеза по-настоящему стали развиваться в последнее время. При создании системы автоматического регулирования поступали обычно следующим образом. Составляли схему системы и, произведя статический расчет ее, подбирали оборудование и аппаратуру. Затем производили анализ переходного процесса в этой системе и устанавливали, насколько он удовлетворяет техническим условиям. Если эти условия не удовлетворялись, в систему вносились коррективы, и она снова анализировалась. После нескольких попыток удавалось создать систему, отвечающую требованиям технических условий. Теперь в случае линейной системы задача может быть решена более совершенным путем. Составляется первоначальная система и строится ее частотная характеристика. Строится также частотная характеристика системы, которая полностью удовлетворяет техническим условиям. По разности полученных частотных характеристик рассчитываются параметры корректирующих элементов, введение которых в систему делает ее отвечающей требованиям технических условий.

Синтезировать подобным образом нелинейные системы в настоящее время не представляется возможным. Имеются системы (следящие системы в военной технике), которые подвергаются случайным воздействиям, не поддающимся типизации. Воздействия в этих случаях обрабатываются статистическими методами, которые применяются при исследовании и расчете систем. Желающих ознакомиться с этим вопросом отсылаем к соответствующей литературе [22].

Рассмотрим подробнее линейные системы. Прежде всего, следует отметить, что абсолютно линейных реальных элементов автоматики не существует. Имеется большое количество элементов, которые без ущерба для точности расчетов могут считаться в некотором достаточно большом диапазоне практически линейными.

линеаризация, основой которой является выдвинутое И. А. Вышнеградским положение о том, что в течение процесса регулирования имеют место лишь достаточно малые отклонения всех изменяющихся величин от установившихся значений. Поэтому криволинейный участок характеристики в окрестностях точки а (рис. 4, 5), соответствующей установившемуся значению переменной, заменяется отрезком касательной, проведенной в этой точке (или иногда секущей, параллельной касательной).

Линеаризация методом касательной аналитически соответствует разложению в ряд Тейлора в точке равновесия функции, описывающей характеристику элемента, и отбрасыванию всех членов, содержащих производные порядка выше первого. При этом внутри рассматриваемого отрезка характеристики, заключающего и точку, соответствующую положению равновесия, функция и все ее производные должны быть непрерывны и однозначны. Наличие зазоров, сухого трения, гистерезиса нарушает непрерывность и однозначность функции. Линеаризовать характеристику в этом случае можно, лишь отбросив эти факторы. Если влияние этих факторов велико и отбросить их нельзя, то линеаризация невозможна и систему нужно исследовать как нелинейную.