и действующим напором в грунте

Зависимость между скоростью фильтрации

Процесс фильтрации в различных дисперсных грунтах протекает по-разному. Для уяснения происходящих в грунте явлений рассмотрим модель грунтовой массы, т.е. водонасыщенного грунта, все поры которого заполнены свободной водой (модель Герсеванова). При этом пренебрежем наличием гидратных оболочек вокруг зерен грунта. Если все поры грунта заполнены водой, то сжатие грунта без возможности бокового расширения может происходить только за счет выдавливания воды из пор (рис.2.15).

Представим себе заполненный водой жесткий сосуд с дырчатым поршнем, поддерживаемым пружиной. Пружина может быть упругая (стальная) или упруговязкая (свинцовая). Если к поршню приложить внешнее усилие P (в кг/см²), то в первый момент вся нагрузка полностью передастся на воду и в воде возникнет гидростатический напор, под действием которого вода начнет выдавливаться через отверстия в поршне. Когда начинается выдавливание воды, пружина вступает в работу интенсивностью P (в Па).

Рис.2.15. Механическая модель сжатия грунтовой массы:

1 – пористый поршень;

2 – пружина (стальная или свинцовая);

3 – вода

На рис.2.16 представлены кривые затухания во времени осадок S=f(t) водонасыщенных грунтов различной фильтрационной способности, загруженных одним и тем же внешним давлением.

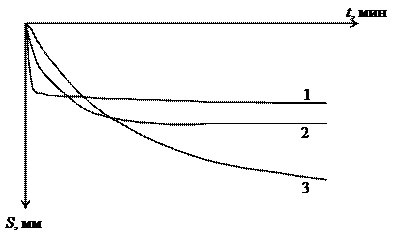
Рис.2.16. Кривые затухания осадок грунта:

1 – песок;

2 – суглинок;

3 – глина

Движение воды в грунте под действием внешней нагрузки происходит под влиянием возникновения в воде гидростатического давления (напора), равного весу столба воды, эквивалентного внешнему давлению Н (в м):

,

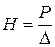где D – удельный вес воды; P – интенсивность внешнего давления.

Опытами ряда исследователей (А.Дарси, Н.Е.Жуковский, Н.Н.Павловский и др.) установлено, что движение воды в средне- и мелкозернистых песках, а также в пластичных глинах, с достаточной для практических целей точностью, можно рассматривать как параллельно-струйное ламинарное движение в пористой среде, подчиняющееся закону Дарси (1885), и пружина будет сжиматься до тех пор, пока между нею и внешней нагрузкой не установится равновесие. Чем крупнее отверстия в поршне, тем этот процесс происходит быстрее.

При снятии нагрузки равновесие пружины нарушается и в воде, находящейся в сосуде, создается отрицательное давление и начинается засасывание воды извне через отверстия поршня, сопровождаемое распрямлением пружины. Если пружина упругая (стальная), то она распрямится полностью, если упруго-вязкая (свинцовая), то частично.

Нечто подобное происходит и в грунтовой массе: в модели пружина изображает скелет грунта, вода - грунтовую воду, отверстия в поршне - капилляры грунта. Модель, разумеется, не отражает полностью сложнейшую природу реальных грунтов, особенно глинистых, с гидратными оболочками вокруг частиц, наличием структурной связности и т.п., но общий ход процесса уплотнения грунтовой массы моделируется достаточно точно.

В любой момент времени в полностью водонасыщенной грунтовой массе

P = P_z + P_w, (2.29)

где P_z – давление в скелете грунта – эффективное давление, P_w – давление в поровой воде – нейтральное давление. Уплотнение грунта происходит только от эффективного давления.

Понятие об эффективном и нейтральном давлениях распространяется на любые нормальные напряжения, действующие в водонасыщенном грунте:

,

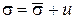откуда

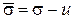. (2.30)

То есть эффективное напряжение 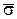равно разности между полным напряжением s и нейтральным напряжением u.

Для всех водонасыщенных грунтов, содержащих в порах свободную воду и лишенных структурной связности, скорость уплотнения грунта под нагрузкой зависит от их водопроницаемости и их фильтрационной способности.

Отмеченное влияние водопроницаемости грунта на скорость протекания процесса уплотнения подтверждают опыты на грунтах с различной фильтрационной способностью, уплотняемых одинаковой внешней нагрузкой

Q = k_ф FJt, (2.31)

где Q – количество воды, м³; k_ф – коэффициент водопроницаемости (фильтрации), м/с; F – площадь сечения грунта, м²; t – время, с; J – гидравлический градиент,

,

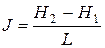где H₂ - H₁– потеря напора, м; L – длина фильтрации, м.

Обозначив 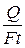через q определим расход воды, отнесенной к единице площади грунта в единицу времени, т.е. скорость фильтрации:

q = k_ф J. (2.32)

При гидравлическом градиенте J=1расход воды q = k_ф, т.е. коэффициент фильтрации есть скорость при градиенте, равном единице.

Таким образом, закон фильтрации может быть сформулирован так: скорость фильтрации воды через грунт прямо пропорциональна гидравлическому градиенту.

Скорость уплотнения грунтовой массы в известных пределах прямо пропорциональна величине коэффициента фильтрации. Поэтому определение водопроницаемости грунтов имеет большое значение для расчета времени протекания осадки зданий и сооружений. Величина коэффициента фильтрации зависит от зернового состава грунта, его пористости и структуры. Каждой ступени нагрузки, передаваемой на грунт, соответствует своя величина пористости, а следовательно, и свой коэффициент фильтрации. При небольших изменениях пористости с достаточной для практической цели точностью можно принять линейную зависимость между коэффициентом фильтрации и коэффициентом пористости.

Средние значения коэффициента фильтрации k_ф (в см/с) при давлении 0,1…0,2 МПа для различных грунтов следующие: для песка i×10^-2… i×10^-4, супеси i×10^-3… i×10^-6, суглинка i×10^-5… i×10^-8, глины i×10^-7… i×10^-10, где i - любое число от 1 до 9. Для перевода размерности из см/сек в см/год следует использовать множитель 3×10⁷.

В лабораторных условиях коэффициент фильтрации определяют путем пропускания воды под напором через образец грунта, предварительно уплотненный заданным давлением. При этом замеряют объем воды, профильтровавшейся через грунт в единицу времени. Величина k_ф, полученная лабораторным путем, может значительно отличаться от характеристик водопроницаемости грунта, полученных в полевых условиях. Полевые испытания, несомненно, дают более точные результаты.

Наличие связанной воды значительно осложняет процесс фильтрации в тонкодисперсных грунтах. Приоритет в исследовании вопроса о фильтрации воды в глинистых грунтах принадлежит российским ученым (Н.П.Пузыревский, Б.В.Дерягин, С.А.Роза, Б.Ф.Рельтов). В 1946 г. Б.Ф.Рельтовым было показано, что глинистые грунты могут быть водопроницаемы, но только лишь при градиентах, превышающих некоторые начальные значения. Для того, чтобы началась фильтрация воды в глинистом грунте, должно быть преодолено вязкое сопротивление сдвигу слоев связанной воды, заполняющей поры. Результаты опытов Б.Ф.Рельтова и С.А.Роза показали отличие закона фильтрации глинистых грунтов от закона Дарси.

На рис.2.17 показана зависимость скорости фильтрации от градиента напора для песчаных и глинистых грунтов. В первом случае прямая выходит из начала координат и скорость фильтрации увеличивается пропорционально увеличению градиента напора; при этом угловой коэффициент прямой представляет собой коэффициент фильтрации. Во втором случае можно выделить три участка графической зависимости:

- участок а, где гидравлический градиент J меньше некоторого значения начального градиента J_n; при этом скорость фильтрации q » 0;

- участок б – J больше J_n; скорость фильтрации при этом пропорциональна градиенту напора:

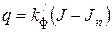, (2.33)

где 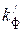не равен коэффициенту фильтрации, получаемому на основании закона Дарси, т.к. прямая не выходит из начала координат;

- участок в, где J больше некоторого значения J_m; фильтрация начинает следовать закону Дарси, т.е. график представляет собой прямую, выходящую из начала координат, при этом скорость фильтрации

q = k_фJ. (2.34)

Рис.2.17. Зависимость между скоростью фильтрации и градиентом напора:

1 – для песков;

2 – для глинистых грунтов

Очевидно, что фильтрация воды в глинистых грунтах, а следовательно, и уплотнение их под действием внешней нагрузки будут происходить лишь в зонах, где величина градиентов напора от внешней нагрузки больше величины начального градиента, свойственной данному роду грунта.

Вода, фильтруясь в порах грунта, оказывает давление на грунтовый скелет. Это давление называется гидродинамическим и относится к внутренним силам, действующим в грунте.

Рассмотрим фильтрацию воды от точки А к точке В через выделенный “грунтовый цилиндр” длиной L и площадью F (рис.2.18). Движение воды происходит под влиянием разности напоров H₁ - H₂.

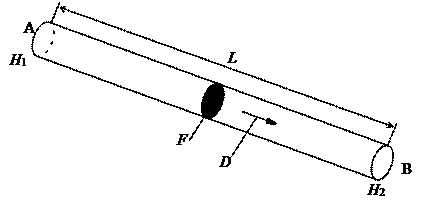
Рис.2.18. Схема гидродинамического давления в скелете грунта

Неуравновешенное давление воды, действующее слева и вызывающее фильтрацию, равно

.

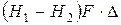Сопротивление фильтрации со стороны грунта равно T×F×L,где Т – сопротивление, отнесенное к единице объема грунта, кН/м³; FL – объем грунтовой призмы.

При обычных ускорениях фильтрации силами инерции фильтрующейся воды можно пренебречь, и тогда давление воды можно считать равным сопротивлению грунта:

,

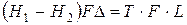откуда

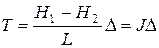, (2.35)

где J – гидравлический градиент.

Гидродинамическое давление D (в кН/м³ или Н/см³) численно равно сопротивлению грунта, но направлено в противоположную сторону:

.

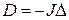Под влиянием гидродинамического давления может происходить разрыхление грунта с выносом частиц из основания, со дна котлована, и выпор грунта из-под фундамента.