Интерференция света. Дифракция.

Краткие сведения из истории оптики.Ответ на вопрос о природе световых волн был получен на основании длин­ного ряда наблюдений над особенностями световых явлений. При этом, как обычно бывает при развитии наших научных воззрений, представление о природе света менялось по мере того, как накапливались новые сведения и данные.

Волновые представления о природе света развивались еще в XVII веке X. Гюйгенсом и поддерживались на про­тяжении XVIII века Л. Эйлером, М. В. Ломоносовым и В. Франклином. Однако в течение всего этого периода наи­более обоснованными оставались корпускулярные представ­ления о свете, в соответствии с которыми свет уподоблялся потоку быстро летящих частичек (И. Ньютон). Лишь в на­чале XIX века трудами О. Френеля и Т. Юнга была надежно обоснована волновая природа света. При этом волны эти уподоблялись упругим волнам, сход­ным до известной степени с волнами, обуславливающими акустические явления. Однако две важные особенности от­личают световые волны от звуковых.

Во-первых, свет распространяется через пространство, откуда удален воздух или другая среда, тогда как звук в вакууме распространяться не может. Распростра­нение света в вакууме можно наблюдать в электрических лампочках накаливания, из баллона которых откачан воз­дух). Другим доказательством способности света распро­страняться в вакууме являются наблюдения света Солнца и звезд, отделенных от нас огромными пространствами, со­держащими в единице объема еще меньше вещества, чем самые совершенные вакуумные приборы. Во-вторых, отличительной особенностью световых волн по сравнению с волнами звуковыми является огромная скорость их распространения. Астрономические наблюдения над затмениями спутников Юпитера, выполненные Ремером, показали, что скорость распространения света в мировом пространстве близка к 300 000 км/с (3×10⁸ м/с). Такова же практически и скорость света в воз­духе, где звук распространяется со скоростью, примерно в миллион раз меньшей.

Огромная скорость распространения света выделяла оптические явления из всех других, известных в первой чет­верти XIX века. Примерно полвека спустя Дж. Максвелл установил, исходя из теоретических соображений, что с та­кой именно скоростью должно распространяться всякое электромагнитное возмущение. Через не­которое время Г. Герц на опыте осуществил электромагнит­ные волны, скорость распространения которых действитель­но оказалась равной скорости распространения света.

Дальнейшими исследованиями и в первую очередь опы­тами П. Н. Лебедева, получившего самые короткие потому времени электромагнитные волны (6 мм), было установле­но, что все основные свойства электромагнитных волн сов­падают со свойствами волн световых. Все эти важные факты привели к мысли, что световые волны представляют собой электромагнитные волны, отличающиеся от волн, обычно применяемых в радиотехнике, своей очень малой длиной (меньше микрометра).

Электромагнитной природой световых волн объясняется испускание электронов освещенными металлами, т. е. так называемый фотоэлектрический эффект. Существует и ряд других явлений, обнаружи­вающих связь между светом и электромагнитными процес­сами. Опираясь на всю совокупность экспериментальных и теоретических данных, мы можем считать установленным, что световые волны представляют собой электромагнитные волны. Светящиеся тела (например, Солнце) испускают электромагнитные (первичные) волны. Попадая на какое-нибудь тело, такая первичная волна вызывает вынужденные колебания его электронов, которые становятся источниками вторичных электромагнитных волн. Все многообразие све­товых явлений, все видимые нами окраски и очертания пред­метов представляют собой суперпозицию (наложение) пер­вичных и вторичных волн. Как уже указывалось раньше, многие черты волновых явлений оказываются сходными для волновых процессов самой разнообразной природы.

В природе и человеческой деятельности волновые процессы широко распространены. Есть волны, образование которых обусловлено силой тяжести. Из-за этого волны, распространяющиеся по поверхности жидкости не являются продольными. Также они и не являются поперечными, так как движение частиц жидкости более сложное. Такие волны на поверхности жидкости имеют сложный продольно-поперечный характер. Несмотря на это они подчиняются закономерностям, которые являются общими для любого волнового процесса, поэтому их очень удобно использовать для наблюдения многих таких закономерностей. Для опытов с такими волнами обычно используют следующую установку. Берут небольшую ванну со стеклянным дном, имеющим площадь 1 м². Под стеклом помещают яркую лампочку, которая позволяет спроецировать процессы, происходящие в этой ванной на потолок или на экран. На тени в увеличенном виде можно наблюдать все явления, происходящие на поверхности воды. Для ослабления отражения волн от бортов ванны их поверхность обычно делают рифленой и сами борта наклонными. Затем, наполняют ванну водой примерно на глубину 1 см и касаются поверхности воды концом проволоки или острием карандаша. От точки прикосновения разбегается кольцевое возмущение. Скорость его распространения достаточно мала (10-30 см/с), поэтому можно легко следить за его перемещением. Далее, получают колебательный процесс следующим образом: укрепляют проволоку на упругой пластинке и заставляют ее колебаться так, чтобы при каждом колебании ее конец ударял по поверхности воды. Во воде побежит система кольцевых возмущений (гребней и впадин). Расстояние между соседними гребнями или впадинами λ, т. е. длина волны, связано с периодом ударов T уже известной формулой λ = vT.

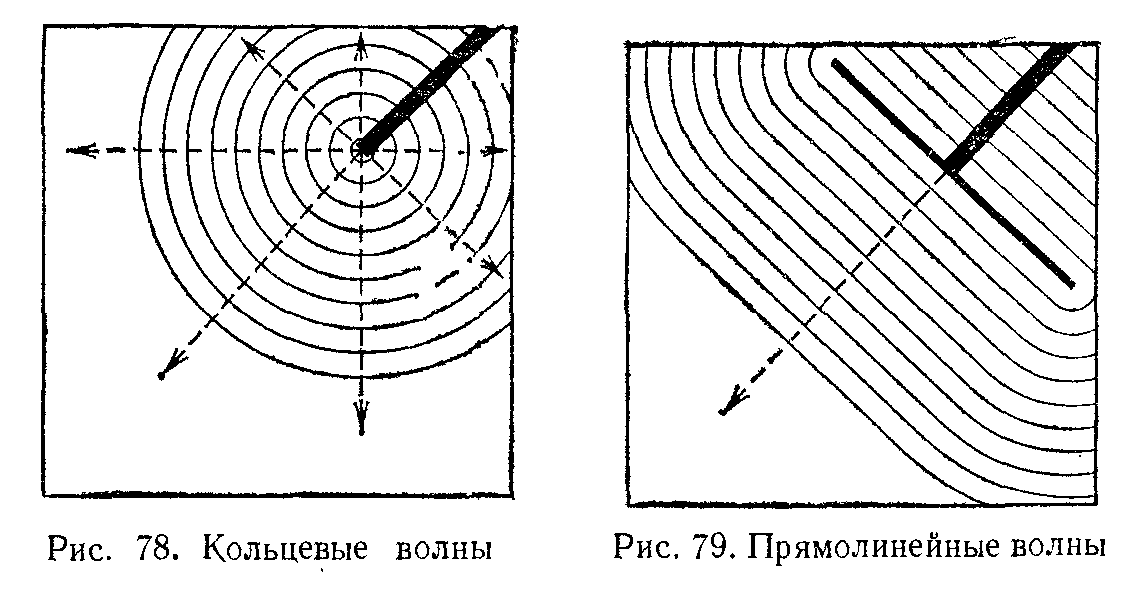
Линии, перпендикулярные к гребням и впадинам показывают направление распространения волны. У кольцевой волны направления распространения изображаются прямыми линиями, расходящимися из центра волны (рис. 78).

Если заменить конец проволоки ребром линейки, параллельным поверхности воды, то можно создать волну, имеющую форму не концентрических колец, а параллельных друг другу прямолинейных гребней и впадин (рис.79). В этом случае перед передней частью линейки мы имеем одно-единственное направление распространения.

Кольцевые и прямолинейные волны на поверхности дают представление о сферических и плоских волнах в пространстве. Небольшой источник звука, излучающий равномерно во все стороны, создает вокруг себя сферическую волну, в которой сжатия и разряжения воздуха расположены в виде концентрических шаровых слоев. Участок сферической волны, малый по сравнению с расстоянием до ее источника, можно приближенно считать плоским. Это относится к волнам любой физической природы. Например, любой участок (в пределах земной поверхности) световых волн, приходящих от звезд, можно рассматривать как плоскую волну. Волны в водяной ванне используются для получения ряда общих представлений, сохраняющих значение и для упругих (в частности, акустических), и для электромагнитных волн.

Распространение механической волны представляет собой последовательную передачу движения от одного участка среды к другому, означает передачу энергии. Эту энергию доставляет источник волны, когда он приводит в движение непосредственно прилегающий к нему слой среды. От этого слоя энергия передается следующему слою и т. д. Таким образом, распространение волны создает в среде поток энергии, распространяющейся от источника. Представление о потоке энергии, переносимой волнами, впервые ввел в 1874 году русский физик Николай Алексеевич Умов. Также он получил и формулу, позволяющую вычислить интенсивность волны. При встрече волны с различного рода телами переносимая ею энергия может произвести работу или превратиться в другие виды энергии.

Энергию, переносимую волной через сечение, площадь которого равна 1 м², за время, равное 1 с, т. е. мощность переносимую через единичное сечение, называют интенсивность волны. Интенсивность сферической волны убывает обратно пропорционально квадрату расстояния от источника. Как правило волны от источника распространяются во все стороны. Если ограничить возможность расхождения волны в стороны, то и убывание интенсивности уменьшится. Например, звуковая волна, распространяющаяся в трубе, имеет большую интенсивность. На этом основано применение переговорных труб, которые использовались на небольших кораблях и служили для связи капитанского мостика с машинным отделением, кабиной рулевого и т. п. Для увеличения громкости звука на больших расстояниях иногда применяют рупоры. Рупор создает направленное излучение. Интенсивность волны, которая распространяется в трубе, не должна была бы уменьшаться с расстоянием, так как энергия здесь переносится через сечения одинаковой площади. На самом деле происходит ослабление волны, вызванное поглощением энергии волны той средой, в которой она распространяется. В каждой точке на пути волны часть той энергии, которую она переносит, тратится на работу против сил трения в среде и переходит в тепло. Электромагнитные волны представляют собой передачу изменений электромагнитного поля. Они тоже переносят энергию, но энергию электрического и магнитного полей. В таком виде на Землю поступает энергия от Солнца.

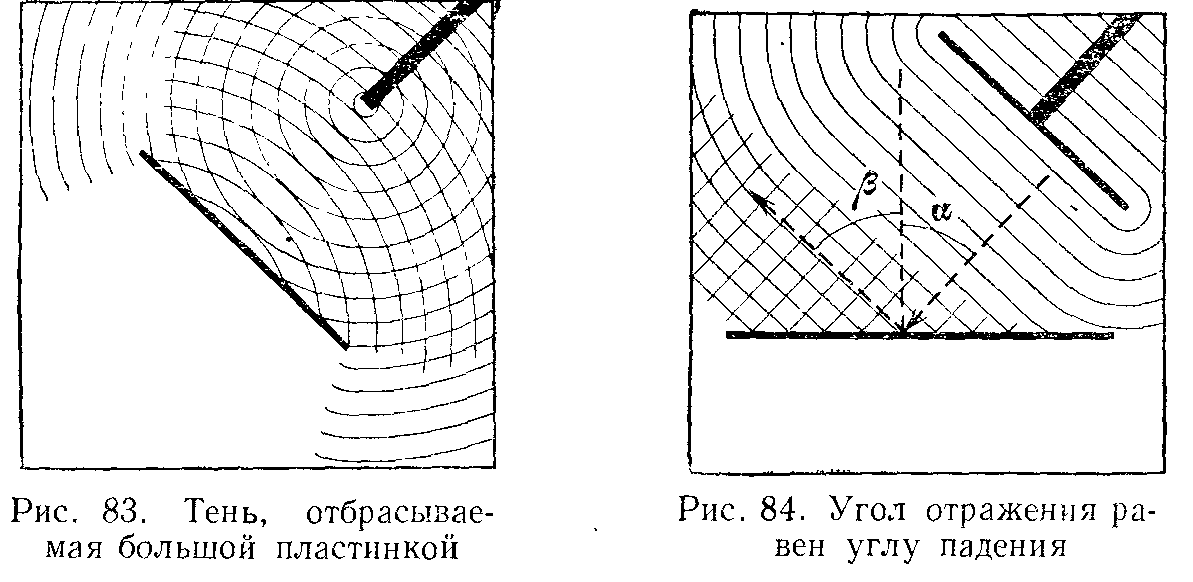Если поставить на пути волн в водяной ванне плоскую пластинку, длина которой велика по сравнению с длиной волны λ, то можно будет наблюдать следующую картину. Позади пластинки получается область, в которой поверхность воды остается почти в покое. Можно сказать, что пластинка создает тень – пространство, куда волны не проникают. Перед пластинкой будет отчетливо видно, как волны отражаются от нее, т. е. волны, падающие на пластинку, создают волны, идущие от пластинки. Этим отраженные волны имеют форму концентрических дуг, разбегающихся как бы из центра, лежащего позади пластинки. Перед пластинкой в таком случае возникает своеобразная сетка из первичных волн, падающих на пластинку и отраженных волн, которые идут навстречу падающим.

В данном случае угол отражения волны от отражающей плоскости равен углу падения. Этот закон является общим волновым законом, т. е. он справедлив для любых волн, в том числе и для звуковых и для световых волн. Отражением волн от препятствий обусловлены многие явления. Например, эхо обусловлено отражением звуковых волн от зданий, холмов, леса и т. п. Если до слушателя доходят звуковые волны, последовательно отразившиеся от ряда препятствий, то получается многократное эхо. Такое же происхождение имеют и раскаты грома. Чаще всего явление отражения можно наблюдать на световых волнах. Отраженная волна всегда в определенной степени ослаблена по сравнению с падающей волной, так как часть энергии падающей волны поглощается тем телом, от поверхности которого происходит отражение. Например, звуковые волна хорошо отражаются твердыми поверхностями (паркет, мрамор) и намного хуже мягкими поверхностями (ковры и прочие). Любой звук прекращается не сразу после того, как замолк его источник, а постепенно. Отражением звука в помещениях обусловлено явление послезвучания, которое называют реверберацией. В пустых помещениях реверберация велика, поэтому наблюдается своеобразная гулкость. Если в помещении много поглощающих поверхностей, то реверберация не наблюдается. Реверберация играет большую роль в архитектурной акустике, так как определяет звуковые качества помещения. Для определенного помещения и определенного рода звука поглощение волн должно подбираться специально.

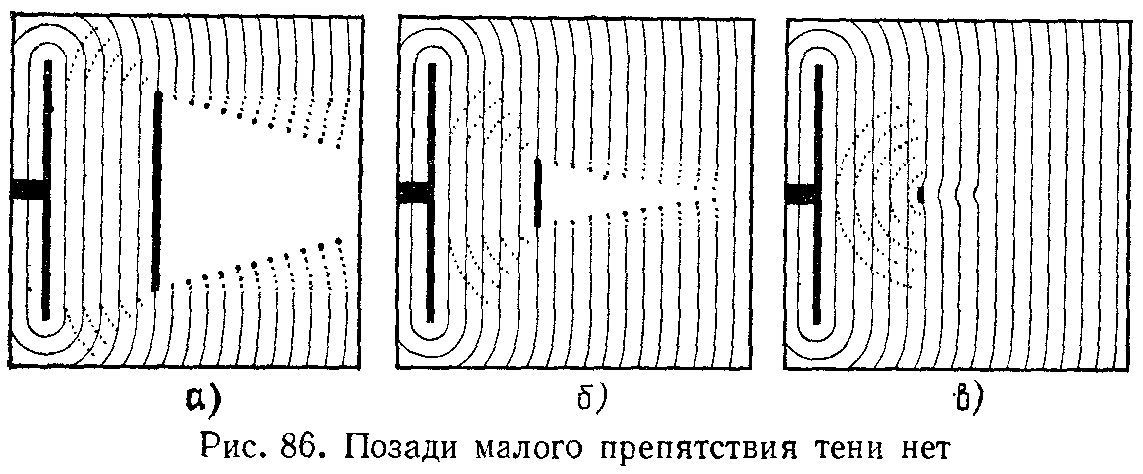Образование тени в случае световых волн – явление, которое можно наблюдать достаточно часто. В случае звуковых волн дело обстоит гораздо хуже. От них очень трудно заслониться. Даже стоя за углом или за забором мы слышим звук. Получается, что эти препятствия не отбрасывают тени (звуковой тени). Таким образом необходимо выяснить, каким образом будет зависеть характер образующейся тени от размеров препятствия. Для этого поставим на пути прямолинейной поверхностной волны в водяной ванне препятствия различного размера (рис. 86).

Получается следующая картина: когда препятствие достаточно велико по сравнению с длиной волны λ, тень от него достаточно резкая, только у самых краев наблюдается небольшое волнение, указывающее, что волна слегка огибает край препятствия. По мере уменьшения препятствия тень оказывается менее ясно выраженной, а когда размеры препятствия становятся сравнимыми с длиной волны, образования тени практически не происходит. Такое огибание волной края препятствий, особенно отчетливо наблюдаемое при малых по сравнению с длиной волны размерах препятствия, называется дифракцией. Именно поэтому при обычных условиях отсутствует «звуковая тень». Дифракцию световых волн наблюдать намного сложнее, так как длины световых волн очень малы – всего несколько десятитысячных долей миллиметра. Из-за дифракции нельзя получить с помощью рупоров, зеркал, отверстий в экранах (диафрагм) и любых других средств сколь угодно узкие волновые пучки.

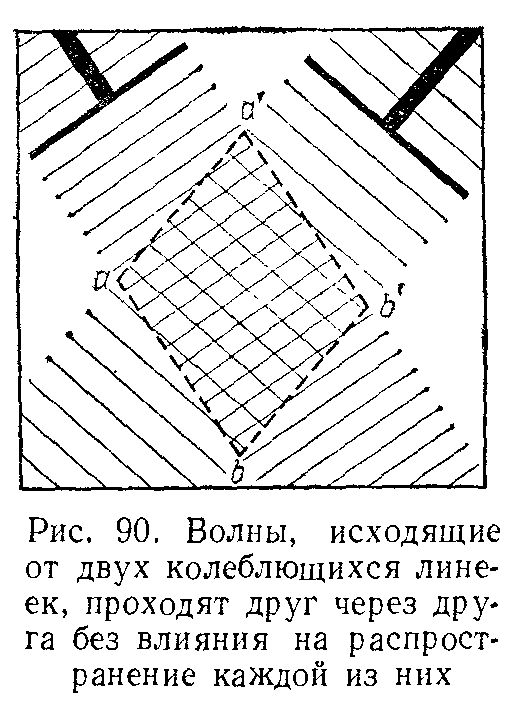
Проделаем следующий опыт с волнами в водяной ванне. Возьмем две упругие пластинки и заставим колебаться на них две линейки, ударяющие по поверхности воды и создающие на ней две плоские волны (рис. 90). Пусть линейки поставлены таким образом, что посылаемые ими волновые пучки пересекаются в области aa`b`b и затем вновь расходятся. В этом случае можно наблюдать, что прохождение каждой из волн через область aa`b`b совершенно не зависит от присутствия или отсутствия другой волны. Никакого влияния одной волны на распространение другой не происходит. То же самое относится и к звуковым волнам: распространение звука от любого источника не испытывает никакого влияния со стороны других звуковых волн, как угодно распространяющихся в это время через те же области среды. Для световых волн справедлива та же закономерность: их распространение от любого предмета к человеческому глазу и все что человек видит благодаря этим волнам не зависит от множества других световых волн, пересекающих по всевозможным направлениям путь света от наблюдаемого предмета. В областях пространства, в которых волны налагаются друг на друга происходит следующее: каждая частица среды, находящаяся на пути волны, совершает колебания с периодом этой волны. Если эта частица находится на пути двух волн, то она одновременно участвует в колебаниях обеих волн, т. е. ее движение представляет собой сумму этих колебаний.

Таким образом, наложение двух (или большего числа) волн есть сложение их колебаний в каждой точке среды, через которую обе эти волны (или все эти волны) проходят. Наложение волн в каком-либо месте не влияет на их распространение как через это место так и вне его.

Однако, если происходит наложение волн одинаковой частоты, которые тогда имеют и одинаковую длину волны, то могут возникнуть некоторые своеобразные и очень важные явления.

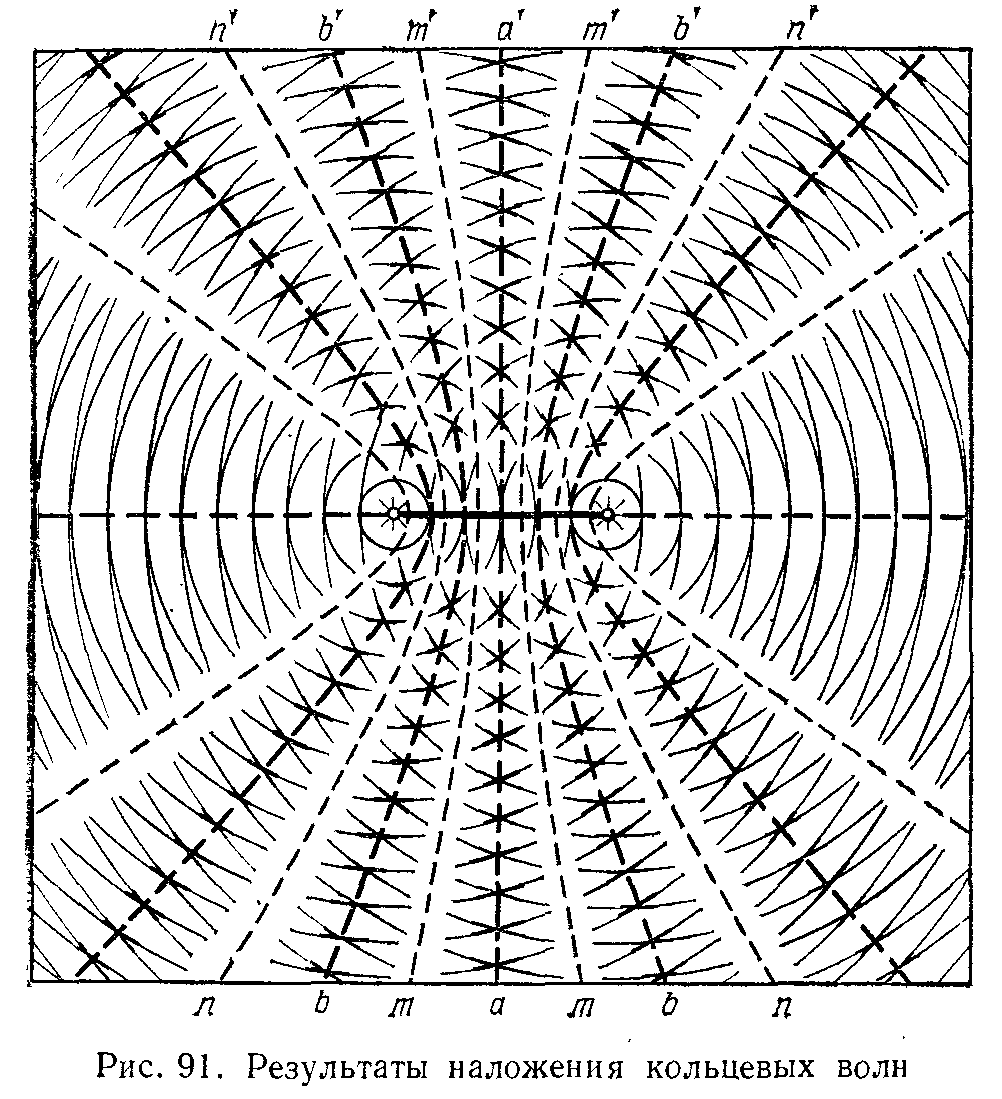
Суть этих явлений можно установить с помощью следующего опыта. Укрепим на колеблющейся пластинке два проволочных острия, которые будут одновременно ударять по поверхности воды в ванне. В итоге, получим две кольцевые волны с одинаковой длиной волны, которые разбегаются из двух центров и налагаются друг на друга. Если расстояние между остриями больше длины волны, то мы получится картина, изображенная на рис. 91. Происходит не просто усиление колебаний воды, а более сложное явление. На поверхности воды получается ряд областей, в которых колебания особенно сильны (максимумы aa`, bb`, …), разделенных областями сильно ослабленного волнения (минимумы mm`, nn`, …). Такая картина чередующихся максимумов и минимумов колебания называется интерференционной картиной, а само явление наложения волн, когда оно приводит к образованию этой картины – интерференцией волн. В каждой точке колебание поверхности воды является суммой колебаний, вызванных каждой волной в отдельности В том месте куда пришли гребни двух волн, то есть обе волны в одинаковой фазе, получится усиленный подъем воды. Через полпериода гребни сменятся впадинами, причем у обеих волн одновременно, так как их период одинаков. Поэтому поверхность воды сильно опустится. В этом месте получается усиленное колебание. В том месте, где волны проходят в противоположных фазах, колебания взаимно ослабятся. Ослабление будет происходить все время, так как в любой момент фазы обеих волн будут противоположны. Таким образом, существенным для возникновения интерференционной картины является то обстоятельство, что волны, идущие из обоих центров, согласованы между собой: сдвиг фаз между колебаниями обеих волн в каждой данной точке остается все время постоянным. Когда говорят об интерференционной картине, имеют в виду устойчивую, не изменяющуюся со временем картину чередования максимумов и минимумов. Такая устойчивая картина возникает лишь в том случае, когда налагающиеся волны имеют одинаковый период и неизменный сдвиг фаз колебаний в каждой точке. Такие волны называются когерентными. Следовательно, устойчивая интерференция может иметь место только при условии когерентности волн.

Энергия излучения. Световой поток.Разнообразные действия света обусловле­ны в первую очередь наличием определенной энергии излу­чения (световой энергии).

Непосредственное восприятие света обусловлено дей­ствием световой энергии, поглощенной чувствительными элементами глаза. То же имеет место и в любом приемнике, способном реагировать на свет, например в фотоэлементе, термоэлементе и фотопластинке. Вследствие этого измере­ния света сводятся к измерению световой энергии или к измерению величин, так или иначе с нею связанных. Отдел оптики, изучающий методы и приемы измерения световой энергии, называется фото­метрией.

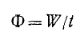
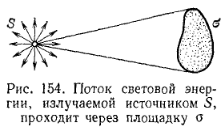Выделим мысленно на пути света, распространяющегося от какого-либо источника 5 (рис. 154), небольшую площад­ку а. Через эту площадку за время t пройдет некоторая энер­гия излучения W. Для того чтобы измерить эту энергию, надо представить себе эту площадку в виде пленки, покры­той веществом, полностью поглощающим всю падающую на него энергию излучения, например сажей, и измерить по­глощенную энергию по нагреванию этой пленки. Отноше­ние

показывает, какая энергия протекает через площадку за единицу времени, и называется потоком излучения (мощ­ностью излучения) через площадку a. Напомним, что мощ­ность, переносимую световой волной через единичную пло­щадку, называют интенсивностью волны.

Поток излучения оценивается в обычных единицах мощ­ности, т. е. в ваттах, а интенсивность излучения — в ваттах на квадратный метр. Однако для восприятия и исполь­зования световой энергии исключительно важную роль иг­рает глаз. Поэтому наряду с энергетической оценкой света пользуются оценкой, основанной на непосредственном све­товом восприятии глаза. Поток излучения, оцениваемый по зрительному ощущению, называется световым потоком.

Таким образом, в световых измерениях используются две системы обозначений и две системы единиц; одна из них ос­нована на энергетической оценке света, другая — на оцен­ке света по зрительному ощущению.

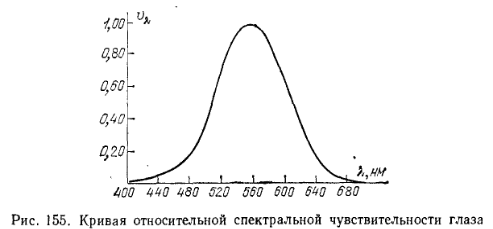Так как чувствительность глаза к свету разной длины волны (разного цвета) весьма различна, то энергетическая оценка света и оценка светового потока по зрительному ощу­щению могут существенно отличаться. Так, при одной и той же мощности излучения зрительное ощущение от лучей зе­леного цвета будет примерно в 100 раз больше, чем от лу­чей красного или сине-фиолетового цвета. Поэтому для зри­тельной оценки световых потоков необходимо знать чув­ствительность глаза к свету различной длины волны или так называемую кривую относи­тельной спектральной чувствительности глаза, изображен­ную на рис. 155. На этой кривой показана относительная чувствительность v_λ человеческого глаза в зависимости от длины волны λ. Кривые чувствительности глаза различных людей не­сколько различны, особенно в области малых чувствительностей. Кривая, приведенная на рис. 155, получена на ос­новании многочисленных измерений; она характеризует чувствительность среднего нормального глаза и утверж­дена Международным комитетом по стандартам.

Точечные источники света. Все вопросы, связанные с определением световых величин, особенно просто решают­ся в том случае, когда источник излучает свет равномерно во всех направлениях. Таким источником является, напри­мер, раскаленный металлический шарик. Подобный шарик посылает свет равномерно во все стороны; световой поток от него распределен равномерно по всем направлени­ям. Это означает, что действие источника на какой-либо при­емник света будет зависеть только от расстояния между приемником и центром светящегося шарика и не бу­дет зависеть от направления радиуса, проведенного к приемнику из центра шарика.

Во многих случаях действие света изучается на расстоя­нии R, настолько превосходящем радиус rсветящегося ша­рика, что размеры последнего можно не учитывать. Тогда можно считать, что излучение света происходит как бы из одной точки — центра светящегося шара. В подобных слу­чаях источник света называется точечным источником.

Само собой разумеется, что точечный источник не явля­ется точкой в геометрическом смысле, а имеет, как и всякое физическое тело, конечные размеры. Источник излучения исчезающе малых размеров не имеет физического смысла, ибо такой источник должен был бы с единицы своей поверх­ности излучать бесконечно большую мощность, что невоз­можно.

Более того, источник, который мы можем считать точеч­ным, не всегда должен быть малым. Дело не в абсолют­ных размерах источника, а в соотношении между его раз­мерами и теми расстояниями от источника, на которых иссле­дуется его действие. Так, для всех практических задач наи­лучшим образцом точечных источников являются звезды; хотя они имеют огромные размеры, расстояния от них до Земли во много раз превосходят эти размеры. Необходимо также помнить, что прообразом точечного источника является равномерно светящийся шарик. Поэтому источник света, посылающий свет неравномерно в разные стороны, не является точечным, хотя бы он был и очень маленьким по сравнению с расстоянием до точки наблюдения.

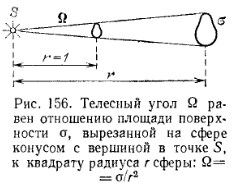
Определим более точно, что понимается под равномерным излучением света во все стороны. Для этого надо воспользоваться представлением о те­лесном угле Ω, который равен отношению площади поверх­ности σ, вырезанной на сфе­ре конусом с вершиной в точ­ке S, к квадрату радиуса rсферы (рис. 156):

Это отношение не зависит от r, так как с ростом rвырезаемая конусом поверхность σ увеличивается пропорциональ­но r². Если r =1, то Ω численно равен σ, т. е. телесный угол измеряется поверхностью, вырезанной конусом на сфере единичного радиуса. Единицей телесного угла является стерадиан (ср) — телесный угол, которому на сфере еди­ничного радиуса соответствует поверхность с площадью, равной единице. Телесный угол, охватывающий все про­странство вокруг источника, равен 4π ср, ибо площадь пол­ной поверхности сферы единичного радиуса есть 4π.

Полное излучение какого-либо источника распределяется в телесном угле 4π ср. Излучение называется равномерным или изотропным, если в одинаковые телесные углы, выде­ленные по любому направлению, излучается одинаковая мощность. Конечно, чем меньше телесные углы, в которых мы производим сравнение мощности, излучаемой источни­ком, тем с большей точностью мы проверяем равномерность излучения.

Таким образом, точечным источником является источник, размеры которого малы по сравнению с расстоянием до места наблю­дения и который посылает световой поток равномерно во все стороны.

Сила света и освещенность.Полный световой поток характеризует излучение, которое распространяется от источника по всем направлениям. Для практиче­ских же целей часто важнее знать не полный световой поток, а тот поток, который идет по определенному направле­нию или падает на определенную площадку. Так, например, автомобилисту важно получить достаточно большой све­товой поток в сравнительно узком телесном угле, внутри которого находится небольшой участок шоссе. Для работаю­щего за письменным столом важен тот поток, который осве­щает стол или даже часть стола, тетрадь или книгу, т. е. поток, приходящийся на некоторую площадь. В соответ­ствии с этим установлены два вспомогательных понятия — сила света (I) и освещенность (Е).

Силой света называют световой поток, рассчитанный на телесный угол, равный стерадиану, т. е. отношение све­тового потока Ф, заключенного внутри телесного угла Q, к этому углу:

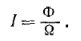
Освещенность же есть световой поток, рассчитанный на единицу площади, т. е. отношение светового потока Ф, па­дающего на площадь а, к этой площади:

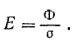
Эти формулы определяют сред­нюю силу света и среднюю освещенность. Они будут тем ближе к истинным, чем равномернее поток или чем мень­ше Ω и σ.

Очевидно, что с помощью источника, посылающего оп­ределенный световой поток, мы можем осуществить весьма разнообразную силу света и весьма разнообразную осве­щенность. Действительно, если направить весь поток или большую его часть внутрь малого телесного угла, то в на­правлении, выделенном этим углом, можно получить очень большую силу света. Так, например, в прожекторах удается сосредоточить большую часть потока, посылаемого электрической дугой, в очень малом телесном угле и полу­чить в соответствующем направлений огромную силу света. В меньшей степени той же цели достигают с помощью авто­мобильных фар. Если сконцентрировать с помощью отража­телей или линз световой поток от какого-либо источника на небольшой площади, то можно достигнуть большой осве­щенности. Так поступают, например, стремясь сильно осве­тить препарат, рассматриваемый в микроскоп; аналогичное назначение выполняет рефлектор лампы, обеспечивающий хорошую освещенность рабочего места.

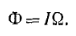Согласно формуле для силы света световой поток Ф равен произ­ведению силы света I на телесный угол Ω, в котором он рас­пространяется;

Если телесный угол Ω = 0, т. е. лучи строго парал­лельны, то световой поток также равен нулю. Это озна­чает, что строго параллельный пучок световых лучей не не­сет никакой энергии, т. е. не имеет физического смысла,— ни в одном реальном опыте не может быть осуществлен стро­го параллельный пучок. Это — чисто геометрическое поня­тие. Тем не менее параллельными пучками лучей очень ши­роко пользуются в оптике. Дело в том, что небольшие отступления от параллельности световых лучей, имеющие с энергетической точки зрения принципиальное значение, в вопросах, связанных с прохождением световых лучей че­рез оптические системы, практически не играют никакой роли. Например, углы, под которыми лучи от удаленной звезды попадают в наш глаз или телескоп, настолько малы, что они даже не могут быть измерены существующими ме­тодами; практически эти лучи не отличаются от параллель­ных. Однако эти углы все же не равны нулю, и именно бла­годаря этому мы и видим звезду. В последнее время свето­вые пучки с очень острой направленностью, т. е. с очень малой расходимостью световых лучей, получают при помощи лазеров. Однако и в этом случае углы между лу­чами имеют конечное значение.

Законы освещенности. Как показывают формулы для силы света и освещенности, величины Е и I связаны между собой.

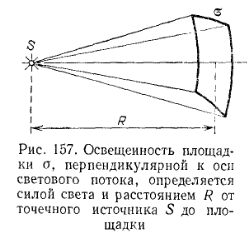
Пусть точечный источник S освещает небольшую пло­щадку а, расположенную на расстоянии R от источника (рис. 157).

Построим телесный угол Ω, вершина которого лежит в точке S и который опирается на края площадки а. Он равен σ/R². Поток, посылаемый источником в этот телесный угол, обозначим через Ф. Тогда сила света I = Ф/Ω = Ф R²/σ , ос­вещенность E = Ф/Ω.

Отсюда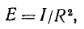

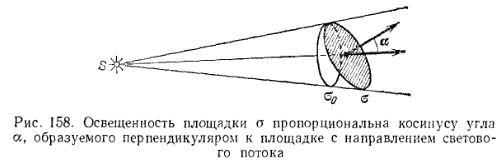т. е. освещенность площадки равна силе света, деленной на квадрат расстояния до точечного источника. Сравнивая освещенности площадок, расположенных на разных расстояниях R_l , R₂ от точечного источника, найдем Е₁/ E₂=R₂²/R_l² и т. д., или т. е. освещенность обратно пропорциональна квадрату рас­стояния от площадки до точечного источника. Это так называемый закон обратных квад­ратов.

Если бы площадка а была расположена не перпендику­лярно к оси потока, а поверну­та на угол а, то она имела бы размеры σ = σ₀/cosα (рис. 158), где σ₀ — площадка, пересе­кающая тот же телесный угол перпендикулярно к оси пуч­ка, так что Ω = σ₀/R². Мы предполагаем площадки σ и σ₀ настолько малыми и столь удаленными от источника, что для всех точек этих площадок расстояние до источника мо­жет считаться одинаковым (R) и лучи во всех точках состав­ляют с перпендикуляром к площадке σ один и тот же угол α (угол падения).

В таком случае, освещенность площадки σ есть:

(*)

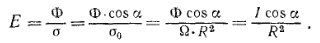Итак, освещенность, создаваемая точечным источником на некоторой площадке, равна силе света, умноженной на ко­синус угла падения света на площадку и деленной на квад­рат расстояния до источника.

Закон обратных квадратов соблюдается вполне строго для точечных источников. Если же размеры источника не очень малы по сравнению с расстоянием до освещаемой поверхности, то соотношение

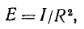не верно и освещен­ность убывает медленнее, чем по закону I/R²; в частности, если размеры светящейся поверхности велики по сравнению с R, то освещенность практически не меняется при измене­нии R. Чем меньше размеры источника d по сравнению с R_t тем лучше выполняется закон обратных квадратов. Так,

при соотношении d/R<(1/10) изменения освещенности

по этой формуле дают вполне хорошее согласие с наблю­дением. Таким образом, закон обратных квадратов можно считать практически выполняющимся, если размеры источ­ника не превышают 0,1 расстояния до освещаемой поверх­ности.

Освещенность поверхности, как видно из формулы (*), зависит, кроме того, от угла, под которым падают на эту поверхность световые лучи.

Единицы световых величин. В системе световых еди­ниц за исходную величину принята единица силы света. Эта единица имеет условный характер: в качестве единицы силы света принята сила света некоторого эталон­ного источника. Таким источником, дающим силу света I = 1, вначале условились считать пламя свечи, изготовлен­ной строго стандартным образом. Однако этот эталонный источник оказался мало удобным, так как даваемая им сила света несколько изменяется по мере образования «нагара» и, кроме того, зависит от температуры и влажности воздуха. Для установления эталона силы света было предложено много других источников, в частности эталонные электри­ческие лампы накаливания, образцы которых хранятся в крупных государственных измерительных лабораториях и контролируются взаимными сравнениями.

Единица силы света называется канделой (кд) — от ла­тинского слова candela, что означает свеча. Кандела равна силе света в заданном направлении источника, испускаю­щего излучение частоты 540×10¹² Гц (длина волны в ваку­уме 555 нм), энергетическая сила света которого в этом на­правлении составляет 1/683 Вт/ср. Кандела является одной из основных единиц Международной системы единиц (СИ). За единицу светового потока принят лю­мен (обозначается лм). Люмен есть световой поток, испус­каемый точечным источником, сила света которого равна 1 кд, внутри единичного телесного угла (т. е. угла, равного 1 ср). Для излучения, соответствующего максимуму спект­ральной чувствительности глаза (А=555 нм), световой по­ток равен 683 люменам, если энергетическая сила света рав­на 1 Вт/ср.

За единицу освещенности принимается ос­вещенность такой поверхности, на 1 м² которой падает све­товой поток 1 лм, равномерно распределенный по площадке. Эта единица освещенности называется люкс (лк). Освещен­ность 1 лм получается на поверхности сферы радиуса 1 м, если в центре сферы помещен точечный источник, сила света которого равна 1 кд.

ВОПРОСЫ К ТЕКСТУ: (КРИТЕРИИ ОЦЕНКИ: 15 ВОПРОСОВ - «3», 20 ВОПРОСОВ – «4», 25-35 ВОПРОСОВ – «5»)

1. Укажите особенности, отличающие световые волны от звуковых.

2. С какой скоростью должно распространяться любое электромагнитное возмущение? Кто из ученых это установил? Кто подтвердил экспериментально?

3. Перечислите факты, которые привели к мысли, что световые волны представляют собой электромагнитные волны, отличающиеся от волн, которые применяются в радиотехнике.

4. Что такое фотоэлектрический эффект?

5. Каким образом электроны становятся источниками вторичных волн?

6. Образование каких волн обусловлено силой тяжести?

7. Какой характер имеют волны на поверхности жидкости?

8. С помощью какой установки можно установить закономерности, общие для всех волновых процессов?

9. Каким образом и с помощью чего можно создать сферическую волну?

10. Что представляет собой сферическая звуковая волна?

11. Когда участок сферической волны можно считать плоским?

12. Каким образом происходит передача энергии от источника в механической волне?

13. Кто ввел представление о потоке энергии, переносимой волной?

14. Что называется интенсивностью волны?

15. Как ведет себя интенсивность волны при удалении от источника?

16. Почему даже в трубе происходит ослабление волны?

17. Какие явления обусловлены отражением волн от препятствий?

18. Что называется реверберацией?

19. Почему после замолкания источника звука сам звук не затихает сразу?

20. Какую роль играет реверберация в архитектурной акустике?

21. Почему звуковая волна в отличие от световой действует даже на человека стоящего за углом или за забором? Объясните, чем это обусловлено.

22. Что такое дифракция волн?

23. Почему сложно наблюдать дифракцию световых волн?

24. Что называется интерференцией волн? Когда интерференционная картина является устойчивой?

25. Какие волны называются когерентными?

26. Что называется мощностью излучения?

27. Что называется интенсивностью волны?

28. Укажите в каких единицах измеряется поток излучения и интенсивность волны.

29. Что такое световой поток?

30. Какой источник волн называется точечным?

31. Укажите единицу измерения телесного угла и нарисуйте сам угол.

32. Какое излучение называется изотропным?

33. Что такое сила света и освещенность?

34. В чем заключается закон обратных квадратов?

35. Укажите световые величины и единицы их измерения.