Топологический элементный анализ
 Независимые от системы элементы формально выглядят как изолированные вершины графа структуры (ее симплекса).
Независимые от системы элементы формально выглядят как изолированные вершины графа структуры (ее симплекса).
Если некоторый элемент на всех структурах данной системы является независимым, то с системно-физической точки зрения он не может рассматриваться как элемент, входящий в состав данной системы.
Наличие или отсутствие изолированных вершин в графе, соответствующем некоторой структуре, можно установить формально с помощью матрицы инциденций W, элементы которой для ориентированного графа определяются следующим образом:
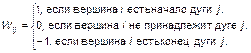 (2.1.35)
(2.1.35)
Для неориентированного графа элементы матрицы инциденций определяются так:
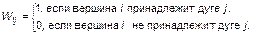 (2.1.36)
(2.1.36)
Таким образом, поиск изолированной вершины сводится к поиску нулевой строки матрицы инциденций.
Входные элементы системы (точнее, подозрительные в этом отношении элементы) соответствуют на графе структуры так называемым висячим вершинам.
Висячей вершиной ориентированного графа называется неизолированная вершина, в которую нельзя попасть ни из какой другой вершины графа, двигаясь по направлению ориентации дуг. В матрице инциденций висячей вершине соответствует строка, в которой нет ни одного отрицательного элемента.
Выходные элементы системы (точнее, подозрительные в этом отношении элементы) соответствуют на графе структуры так называемым тупиковым вершинам.
Тупиковой называется такая неизолированная вершина ориентированного графа, из которой нельзя попасть ни в какую другую вершину графа, двигаясь в направлении ориентации дуг. В матрице инциденций тупиковой вершине отвечает строка, в которой нет ни одного положительного элемента.
Наличие изолированных, висячих и тупиковых вершин формально может быть установленно также с помощью матрицы смежности V , элементы которой определяются следующим образом:
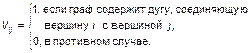 (2.1.37)
(2.1.37)
Процедура поиска особых вершин выполняется так. Первоначально вычисляется сумма элементов для каждой отдельно взятой строки 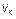 и для каждого отдельно взятого столбца
и для каждого отдельно взятого столбца 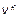 :
:
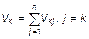 , (2.1.38)
, (2.1.38)
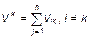 . (2.1.39)
. (2.1.39)
Далее используются следующие очевидные правила:
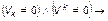 (вершина k внутренняя), (2.1.40)
(вершина k внутренняя), (2.1.40)
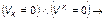 (вершина k висячая), (2.1.41)
(вершина k висячая), (2.1.41)
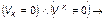 (вершина k тупиковая), (2.1.42)
(вершина k тупиковая), (2.1.42)
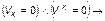 (вершина k изолированная). (2.1.43)
(вершина k изолированная). (2.1.43)
Дата добавления: 2016-12-08; просмотров: 1088;
