Информационно-статистическая теория голосований
 Социально-экономические системы относятся к классу больших систем. Это – системы, состоящие из достаточно большого числа примерно равносущественных для них элементов. Важной их особенностью является то, что обменные взаимодействия их элементов, подчиняющихся определенным ценностным принципам, в силу массовости своего проявления, порождают некоторые статистические закономерности, имеющие значительный практический интерес.
Социально-экономические системы относятся к классу больших систем. Это – системы, состоящие из достаточно большого числа примерно равносущественных для них элементов. Важной их особенностью является то, что обменные взаимодействия их элементов, подчиняющихся определенным ценностным принципам, в силу массовости своего проявления, порождают некоторые статистические закономерности, имеющие значительный практический интерес.
Статистические закономерности поведения элементов большой системы отражают соответствующие интегративные свойства последней, при этом они выступают уже не просто в роли некоторых особенностей (закономерностей), а в роли законов, определяющих в той или иной мере бытие данной системы в целом и вытекающих из вполне определенных общих ценностных принципов существования.
 Наиболее фундаментальным из указанных принципов является принцип максимума информации, фиксируемой в информационном сообщении системы внешнему окружению:
Наиболее фундаментальным из указанных принципов является принцип максимума информации, фиксируемой в информационном сообщении системы внешнему окружению:
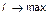 .
.
Это сообщение снижает неопределенность состояния системы относительно внешнего наблюдателя.
Если сообщение отвечает жестко фиксированному состоянию и вполне определенно, то принцип максимума информации есть принцип максимума энтропии априорного (до фиксации в сообщении) состояния системы
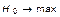 .
.
В качестве примера использования принципа максимума информации для анализа статистических закономерностей в интерактивных больших системах рассмотрим следующую задачу о голосовании.
 Пусть на одно или несколько мест в некоторой общественной иерархии претендует m кандидатов, каждый из которых в результате голосования набирает соответствующее ему количество голосов избирателей (респондентов). Если голосование осуществляется в форме опроса, то в качестве «кандидатов» могут выступать не только известные личности, претендующие на то или иное место в общественном мнении, но и проблемы, волнующие те или иные социальные группы.
Пусть на одно или несколько мест в некоторой общественной иерархии претендует m кандидатов, каждый из которых в результате голосования набирает соответствующее ему количество голосов избирателей (респондентов). Если голосование осуществляется в форме опроса, то в качестве «кандидатов» могут выступать не только известные личности, претендующие на то или иное место в общественном мнении, но и проблемы, волнующие те или иные социальные группы.
Упорядочим кандидатов в порядке убывания количества голосов, отданных за них, т.е. примем
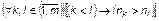 ,
,
где 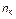 – количество голосов, поданных за кандидата К.
– количество голосов, поданных за кандидата К.
Будем предполагать, что выборы обеспечивают свободное и независимое волеизъявление избирателей и полное информационное равноправие кандидатов. Предварительно рассмотрим случай ценностной неразличимости кандидатов в глазах избирателей.
Исходя из принципа максимума информации, фиксируемой в состоянии избирательной системы (системы респондентов) относительно внешнего наблюдателя в результате голосования (опроса), можно записать:
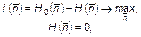 (1.4.18)
(1.4.18)
где 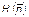 – энтропия результатов голосования;
– энтропия результатов голосования; 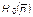 – энтропия исходного состояния избирательной системы, связанная с неопределенностью распределения числа голосов избирателей
– энтропия исходного состояния избирательной системы, связанная с неопределенностью распределения числа голосов избирателей 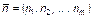 по местам, которые могут занять кандидаты в результате голосования.
по местам, которые могут занять кандидаты в результате голосования.
Используя вероятностную меру энтропии, предыдущее выражение можно записать в виде
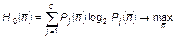 , (1.4.19)
, (1.4.19)
где C – общее число возможных комбинаций голосов конкретных избирателей, соответствующих данному распределению 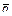 ;
; 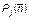 – априорная вероятность данной конкретной комбинации голосов избирателей, отвечающих распределению
– априорная вероятность данной конкретной комбинации голосов избирателей, отвечающих распределению 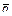 .
.
Поскольку все комбинации голосов конкретных избирателей, т.е. все микросостояния избирательной системы априори для внешнего наблюдателя, не знакомого с их индивидуальными предпочтениями, равновозможны, и поскольку до момента подсчета голосов не известно, за какое место (не кандидата, а именно место) отдал свой голос тот или иной избиратель, то можно считать, что априорные вероятности 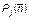 равны между собой, т.е. для всех
равны между собой, т.е. для всех 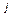
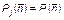 . (1.4.20)
. (1.4.20)
В силу принятого выше предположения о независимости волеизъявления отдельных избирателей вероятность 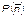 конкретной комбинации голосов, соответствующей распределению
конкретной комбинации голосов, соответствующей распределению 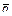 , будет, очевидно, равна
, будет, очевидно, равна


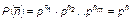 , (1.4.21)
, (1.4.21)
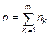 , (1.4.22)
, (1.4.22)
где n – общее число проголосовавших избирателей; p – вероятность того, что голос отдельно взятого конкретного избирателя будет отдан за кандидата, который в результате голосования займет некоторое конкретное место. В силу сделанных выше предположений эти вероятности одинаковы для всех пар «избиратель-место» и равны 1/m.
Таким образом,
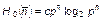 , (1.4.23)
, (1.4.23)
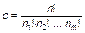 , (1.4.24)
, (1.4.24)
где с – общее число возможных комбинаций распределения голосов конкретных избирателей по местам, которые займут предпочитаемые ими кандидаты.
Нетрудно видеть, что в рассматриваемой ситуации принципу максимума информации 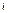 (энтропии
(энтропии 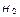 ) отвечает наиболее вероятное распределение числа голосов избирателей. Обозначив постоянную величину
) отвечает наиболее вероятное распределение числа голосов избирателей. Обозначив постоянную величину 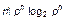 через A, указанный принцип можно записать в следующем виде:
через A, указанный принцип можно записать в следующем виде:
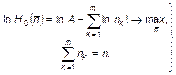 (1.4.25)
(1.4.25)
Используя метод неопределенных множителей Лагранжа и основываясь на формуле Стирлинга
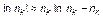 ,
,
справедливой при достаточно больших 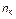 , получим
, получим
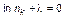 , (1.4.26)
, (1.4.26)
где 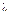 – неопределенный множитель Лагранжа. С учетом предыдущего равенства
– неопределенный множитель Лагранжа. С учетом предыдущего равенства
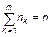
находим
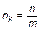 . (1.4.27)
. (1.4.27)
Равномерное распределение (1.4.27) в случае ценностной неразличимости кандидатов является вполне очевидным.
 Рассмотрим теперь случай, когда кандидаты являются ценностно различными в глазах избирателей (респондентов).
Рассмотрим теперь случай, когда кандидаты являются ценностно различными в глазах избирателей (респондентов).
Ценностная различимость означает,что индивид, занимающий то или иное общественное положение, имеет возможность влиять некоторым образом на существующую ситуацию и в силу этого обладает соответствующей социальной ценностью (энергией). Точно так же и решение той или иной проблемы, интересующей граждан, имеет для последних соответствующее значение, а значит, обладает определенной реальной ценностью. В этом смысле ценность кандидатов потенциальна, в отличие от ценности депутатов или решенных проблем.
В силу того, что избирательная система (например, избирательный округ) в момент голосования информационно замкнута (агитация запрещена), то суммарная ценность (социальная энергетика) всех кандидатов есть величина постоянная. Таким образом, можем записать
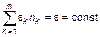 , (1.4.28)
, (1.4.28)
где 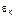 – средняя ценность (энергия) кандидата, занявшего k-е место, в глазах одного избирателя, проголосовавшего за него.
– средняя ценность (энергия) кандидата, занявшего k-е место, в глазах одного избирателя, проголосовавшего за него.
Очевидно, что чем ближе кандидат к первому месту, тем больше должна быть изменена его кажущаяся ценность, чтобы он в общественном мнении поднялся еще на одну ступень. Будем предполагать, что относительное продвижение по этой лестнице общественной значимости пропорционально приращению кажущейся ценности кандидата в расчете на одного избирателя (респондента), отдающего за него свой голос.
Для удобства шкалу общественной значимости X будем считать непрерывной. Тогда сформулированное выше предположение можно записать в виде
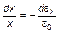 , (1.4.29)
, (1.4.29)
где 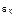 – ценность кандидата, имеющего положение
– ценность кандидата, имеющего положение 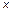 ,
, 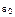 –некоторая постоянная (характеристическая социальная температура системы образов кандидатов). Заметим, что
–некоторая постоянная (характеристическая социальная температура системы образов кандидатов). Заметим, что 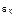 ,
, 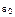 и
и 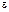 имеют энергетический смысл.
имеют энергетический смысл.
Откуда
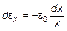 .
.
Интегрируя (1.4.29) по 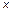 от
от 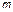 до
до 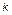 в предположении
в предположении 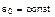 , получаем
, получаем
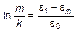 . (1.4.30)
. (1.4.30)
Данное выражение напоминает известный закон Бернулли, связывающий ощущение полезности с количеством имеющихся у индивида денег. В данном случае мы можем говорить о том, что социальная ценность (энергетика, т.е. возможности индивида) нарастает значительно медленнее, чем растет его статус. Из (1.4.30) имеем
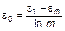 . (1.4.31)
. (1.4.31)
Используя выражение (1.4.30), формулу (1.4.28) преобразуем к виду
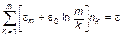 . (1.4.32)
. (1.4.32)
Таким образом, общая постановка задачи определения наиболее вероятного распределения числа голосов избирателей (респондентов) по местам кандидатов будет выглядеть так:
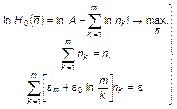 (1.4.33)
(1.4.33)
Поступая аналогично предыдущему, находим
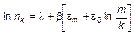 , (1.4.34)
, (1.4.34)
где 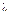 и
и 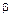 – неопределенные множители Лагранжа. Полученное распределение напоминает известное распределение Максвелла–Больцмана, поэтому величину
– неопределенные множители Лагранжа. Полученное распределение напоминает известное распределение Максвелла–Больцмана, поэтому величину 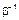 можно рассматривать как характеристическую социальную температуру общества (в энергетическом, ценностном представлении).
можно рассматривать как характеристическую социальную температуру общества (в энергетическом, ценностном представлении).
Так как 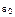 ,
, 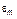 ,
, 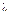 и
и 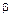 являются постоянными величинами, то последнее выражение может быть представлено в виде, совпадающем с известным эмпирическим законом Суховольского:
являются постоянными величинами, то последнее выражение может быть представлено в виде, совпадающем с известным эмпирическим законом Суховольского:
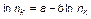 , (1.4.35)
, (1.4.35)
где 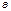 и
и 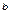 некоторые постоянные.
некоторые постоянные.
Очевидно
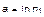 , (1.4.36)
, (1.4.36)
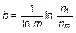 . 1.4.37)
. 1.4.37)
Выражение (1.4.35) эквивалентно
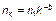 . (1.4.38)
. (1.4.38)
 Одним из важнейших принципов систематики, воплощающих идею системно-физического подхода, является требование согласованности формальной теории с эмпирическими данными. Согласно (1.4.35), распределение числа голосов избирателей (респондентов) по местам, занимаемым кандидатами в однородной по составу избирательной системе, со свободным волеизъявлением каждого избирателя и информационным равноправием всех кандидатов является логически линейным. Этот вывод довольно хорошо согласуется с опытом (рис. 1.4.7). На рисунке приведены результаты выборов 12 декабря 1993 г. по 119-му одномандатному округу Нижегородской области (величина
Одним из важнейших принципов систематики, воплощающих идею системно-физического подхода, является требование согласованности формальной теории с эмпирическими данными. Согласно (1.4.35), распределение числа голосов избирателей (респондентов) по местам, занимаемым кандидатами в однородной по составу избирательной системе, со свободным волеизъявлением каждого избирателя и информационным равноправием всех кандидатов является логически линейным. Этот вывод довольно хорошо согласуется с опытом (рис. 1.4.7). На рисунке приведены результаты выборов 12 декабря 1993 г. по 119-му одномандатному округу Нижегородской области (величина 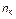 здесь и далее дается в процентах от
здесь и далее дается в процентах от 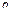 ).
).
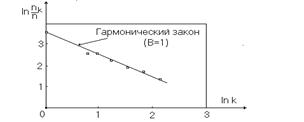
Рис. 1.4.7. Типичный вид зависимости ln nk от ln k при свободном,
независимом волеизъявлении избирателей
и полном информационном равноправии кандидатов
Рассмотрим теперь ситуацию, когда кандидаты информационно неравнозначны. Не трудно видеть, что в данном случае параметры 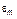 и
и 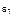 для кандидатов, обладающих различной известностью среди избирателей, будут различны. Пусть, например, имеется всего две группы кандидатов: известные и малоизвестные. Первая группа характеризуется существенно большим значением
для кандидатов, обладающих различной известностью среди избирателей, будут различны. Пусть, например, имеется всего две группы кандидатов: известные и малоизвестные. Первая группа характеризуется существенно большим значением 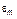 , чем вторая. Вполне очевидно, что малоизвестные кандидаты будут занимать самые последние места. Таким образом, закон распределения числа голосов избирателей (респондентов) будет теперь выглядеть так:
, чем вторая. Вполне очевидно, что малоизвестные кандидаты будут занимать самые последние места. Таким образом, закон распределения числа голосов избирателей (респондентов) будет теперь выглядеть так:
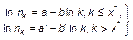 (1.4.39)
(1.4.39)
Величины 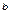 и
и 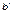 в общем случае также могут не совпадать. Практический опыт подтверждает этот вывод (рис. 1.4.8). На рисунке приведены результаты выборов 12 декабря 1993 г. по 122-му одномандатному округу Нижегородской области.
в общем случае также могут не совпадать. Практический опыт подтверждает этот вывод (рис. 1.4.8). На рисунке приведены результаты выборов 12 декабря 1993 г. по 122-му одномандатному округу Нижегородской области.
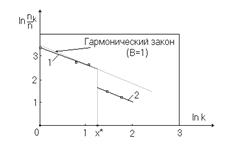
Рис. 1.4.8. Типичный вид зависимости ln nk от ln k при нарушении условий информационного равновесия кандидатов
(равных возможностей самопроявления в глазах избирателей)
Разрыв линии 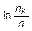 в точке
в точке 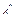 свидетельствует об информационном неравноправии участников избирательной кампании (кандидаты участка 1 имели явно большие возможности, чем кандидаты участка 2, что фактически подтверждается данными финансовых отчетов кандидатов этого округа).
свидетельствует об информационном неравноправии участников избирательной кампании (кандидаты участка 1 имели явно большие возможности, чем кандидаты участка 2, что фактически подтверждается данными финансовых отчетов кандидатов этого округа).
В случае, если некоторые кандидаты или партии (общественные организации) в предвыборной кампании пытаются привлечь внимание избирателей к достаточно узким, частным проблемам, в зависимости 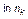 от
от 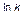 наблюдается резкий излом. Формально для закона (1.4.39) имеем:
наблюдается резкий излом. Формально для закона (1.4.39) имеем:
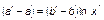 ,
,
где 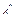 может быть и нецелым числом. Эта закономерность также подтверждается практическим опытом (рис. 1.4.9). На рисунке представлены результаты выборов 12 декабря в Государственную Думу по спискам политических партий и общественных организаций.
может быть и нецелым числом. Эта закономерность также подтверждается практическим опытом (рис. 1.4.9). На рисунке представлены результаты выборов 12 декабря в Государственную Думу по спискам политических партий и общественных организаций.
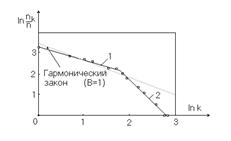
Рис. 1.4.9. Типичный вид зависимости ln nk от ln k
в случае неоднородного по составу множества кандидатов
На участке 1 зависимости 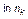 от
от 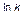 расположены партии и объединения общероссийского масштаба (такие, как ЛДПР, «Выбор России», КПРФ и др.), имеющие широкие политические и экономические позиции. На участке 2 – партии и объединения, занимающие достаточно узкие позиции (например, «Будущее России – новые имена», «Достоинство и милосердие», «Кедр» и т.д.).
расположены партии и объединения общероссийского масштаба (такие, как ЛДПР, «Выбор России», КПРФ и др.), имеющие широкие политические и экономические позиции. На участке 2 – партии и объединения, занимающие достаточно узкие позиции (например, «Будущее России – новые имена», «Достоинство и милосердие», «Кедр» и т.д.).
Поскольку, как уже отмечалось, случайные отклонения от полученного закона есть событие маловероятное (и эта вероятность резко убывает с увеличением такого отклонения), то любое возникаюшее в результате выборов или опроса существенное отклонение можно рассматривать как следствие определенных нарушений (свободы и независимости волеизъявления избирателей (респондентов), информационного равноправия кандидатов и т.п.). К сожалению, такие эффекты на практике встречаются довольно часто (рис. 1.4.10). На рисунке приведены результаты выборов 12 декабря 1993 г. по 117-му одномандатному округу Нижегородской области. Здесь точка A обозначает явно неслучайный выброс, но такой вывод справедлив лишь в предположении справедливости сформулированного выше закона.
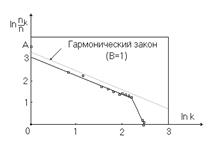
Рис. 1.4.10. Типичный вид зависимости ln nk от ln k
при наличии выбросов (нарушений в системе голосования)
Aнализ многочисленных эмпирических данных выявил еще одну весьма любопытную особенность в зависимости 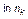 от
от 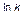 . Оказалось, что среднее положение точки излома логарифмической прямой совпадает с
. Оказалось, что среднее положение точки излома логарифмической прямой совпадает с 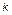 = 7. Складывается впечатление, что избиратели достаточно уверенно могут различать лишь не более 7 уровней в градации ценностей. Далее начинаются случайные флуктуации. Разумеется, этот факт необходимо учитывать при проведении каких-либо опросов или выборов.
= 7. Складывается впечатление, что избиратели достаточно уверенно могут различать лишь не более 7 уровней в градации ценностей. Далее начинаются случайные флуктуации. Разумеется, этот факт необходимо учитывать при проведении каких-либо опросов или выборов.
Согласно описанным выше модельным представлениям при равенстве нулю произведения 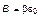 , распространение числа голосов избирателей становится равномерным. Практически такая ситуация может возникнуть по нескольким причинам. Во-первых, если образы кандидатов тождественны друг другу (кандидаты-двойники), что приводит к выполнению равенства
, распространение числа голосов избирателей становится равномерным. Практически такая ситуация может возникнуть по нескольким причинам. Во-первых, если образы кандидатов тождественны друг другу (кандидаты-двойники), что приводит к выполнению равенства 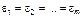 и, следовательно,
и, следовательно, 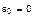 . Во-вторых, если избиратели настолько плохо информированы о предложенных им кандидатах, что свой выбор они совершают случайно. И это приводит также к выполнению равенств
. Во-вторых, если избиратели настолько плохо информированы о предложенных им кандидатах, что свой выбор они совершают случайно. И это приводит также к выполнению равенств 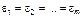 и
и 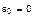 . В-третьих, если избиратели совершенно безразличны к проблемам, которые могут быть решены в результате голосования, то выполняется равенство
. В-третьих, если избиратели совершенно безразличны к проблемам, которые могут быть решены в результате голосования, то выполняется равенство 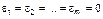 , и
, и 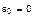 . И, наконец, в-четвертых, если проблемы, затрагиваемые каждым кандидатом, настолько важны для избирателей, а образы кандидатов ценностно различимы, однако в силу высокой напряженности ситуации и желания «сразу всего» избиратели совершат свой выбор случайно. В последнем случае характеристическая температура
. И, наконец, в-четвертых, если проблемы, затрагиваемые каждым кандидатом, настолько важны для избирателей, а образы кандидатов ценностно различимы, однако в силу высокой напряженности ситуации и желания «сразу всего» избиратели совершат свой выбор случайно. В последнем случае характеристическая температура 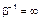 . Заметим, что подобные ситуации могут возникать в некоторых физических системах. Например, из квантовой статистики известно, что равномерное распределение частиц по энергетическим уровням соответствует температуре, равной
. Заметим, что подобные ситуации могут возникать в некоторых физических системах. Например, из квантовой статистики известно, что равномерное распределение частиц по энергетическим уровням соответствует температуре, равной 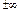 .
.
 Очевидно, что полному термодинамическому равновесию указанных систем будет соответствовать условие равенства их температур
Очевидно, что полному термодинамическому равновесию указанных систем будет соответствовать условие равенства их температур
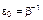 . (1.4.40)
. (1.4.40)
Равенство температур приводит нас к идеальному гармоническому закону распределения числа голосов избирателей по местам
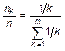 , (1.4.41)
, (1.4.41)
или
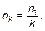 (1.4.42)
(1.4.42)
И, как ни удивительно, рассматриваемая закономерность достаточно хорошо подтверждается опытом (рис. 1.4.11).

Рис. 1.4.11. Гармонический закон голосования
(выборка из 526 данных по различным выборам 1993–1998 гг.)
Идеальный закон распределения числа голосов избирателей соответствует полной гармонии между сообществом избирателей (респондентов) и системой кандидатов (адекватности системы образов последних ценностным представлениям этого сообщества). Отклонения от этого идеального гармонического закона, помимо явных нарушений, могут быть также связаны с наличием среди кандидатов «двойников», ценностные образы которых в глазах избирателей во многом совпадают. Это приводит, по-существу, к тому, что вместо одного претендента на определенное общественное положение мы имеем несколько. Вследствие этого соответствующее число голосов делится между указанными «двойниками», искажая общую картину.
Из сказанного также следует, что существующие демократические механизмы выборов нарушают гармонию между обществом и выборным органом, состояние которого уже не отражает всего спектра социально значимых ценностей. И в этом заключается одно из глубинных противоречий между обществом и представительной властью.
В заключение необходимо отметить, что существенное влияние на отклонения в системе голосований оказывают не только социально-политические, информационные, но экономические и другие факторы. Анализ подобных зависимостей для множества избирательных участков (округов) позволяет, в принципе, установить (объективно) наличие или отсутствие целенаправленной манипуляции со стороны тех или иных политических сил.
 Поскольку гармонический закон выполняется в среднем, то большой интерес вызывает вопрос о виде закона распределения случайных величин отношений n1/nk от
Поскольку гармонический закон выполняется в среднем, то большой интерес вызывает вопрос о виде закона распределения случайных величин отношений n1/nk от 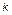 . Не менее актуальным является вопрос о характере искажений гармонического закона, возникающих в результате нарушений отмеченных выше условий.
. Не менее актуальным является вопрос о характере искажений гармонического закона, возникающих в результате нарушений отмеченных выше условий.
Предположим первоначально, что выборы проводятся в полном соответствии с перечисленными выше условиями так, что гармонический закон в среднем выполняется. С целью объединения неоднородных данных по отношениям n1/nk, соответствующим различным 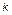 , введем новую обобщенную случайную величину
, введем новую обобщенную случайную величину
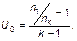 (1.4.43)
(1.4.43)
Очевидно, что независимо от номера 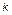 случайная величина
случайная величина 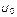 может принимать значения в пределах от 0 до
может принимать значения в пределах от 0 до 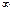 (т.к.
(т.к. 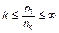 ). Причем ее среднее значение в силу принятых допущений равно
). Причем ее среднее значение в силу принятых допущений равно
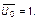 (1.4.44)
(1.4.44)
Функцией распределения, обладающей соответствующими свойствами, является, в частности,
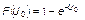 (1.4.45)
(1.4.45)
Плотность распределения, соответствующая этому закону, очевидно, равна
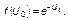 (1.4.46)
(1.4.46)
Целесообразность выбора в качестве теоретического экспоненциального закона распределения отношений голосов подтверждается результатами анализа многочисленных эмпирических данных (рис. 1.4.12–1.4.13).
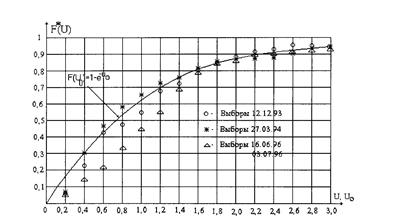
Рис. 1.4.12
Закон распределения (1.4.45) в содержательном плане отвечает хаосу, т.е. отсутствию последствий при проявлении очередных значений 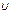 . При выполнении условий, обеспечивающих реализацию гармонического закона, это действительно так, поскольку результаты голосований различных избирателей, опускающих бюллетени в урну, в последовательные моменты времени являются независимыми.
. При выполнении условий, обеспечивающих реализацию гармонического закона, это действительно так, поскольку результаты голосований различных избирателей, опускающих бюллетени в урну, в последовательные моменты времени являются независимыми.
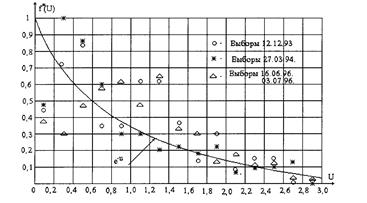
Рис. 1.4.13
Таким образом, гармонический закон голосований и закон распределения (1.4.45) случайных отклонений являются связанными. При выполнении второго из них автоматически выполняется первый. Отсюда следует, что представление результатов голосований в виде совокупности значений или эмпирического закона распределения обобщенной совокупной величины 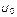 наиболее целесообразно с точки зрения оценки качества организации процесса как предвыборной кампании, так и непосредственно самих выборов. Использование величин
наиболее целесообразно с точки зрения оценки качества организации процесса как предвыборной кампании, так и непосредственно самих выборов. Использование величин 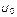 дает возможность (как отмечалось выше) обрабатывать разнородные эмпирические данные совместно, что в силу значительного увеличения объема выборки может существенно повысить точность получаемых оценок качества процесса голосования.
дает возможность (как отмечалось выше) обрабатывать разнородные эмпирические данные совместно, что в силу значительного увеличения объема выборки может существенно повысить точность получаемых оценок качества процесса голосования.
 Вполне очевидно, что в случае нарушения перечисленных выше, а также некоторых других условий голосования (например, отсутствия кандидатов-двойников, отсутствия информационных манипуляций в пользу каких-либо индивидов, соответствия образов множества кандидатов ценностным представлениям избирателей) функция (закон) распределения
Вполне очевидно, что в случае нарушения перечисленных выше, а также некоторых других условий голосования (например, отсутствия кандидатов-двойников, отсутствия информационных манипуляций в пользу каких-либо индивидов, соответствия образов множества кандидатов ценностным представлениям избирателей) функция (закон) распределения 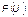 случайной величины
случайной величины
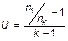 (1.4.47)
(1.4.47)
будет искажаться относительно закона (1.4.45). Как показывают результаты анализа разнообразных по своему характеру (голосования, опросы и т.п.) эмпирических данных (рис. 1.4.12–1.4.13), указанные нарушения внешне проявляются в перераспределении голосов избирателей (респондентов) на множестве возможных альтернатив выбора (включая отказ от голосования и голосование против всех альтернатив).
Помимо отмеченного, определенный вклад в искажение общей картины вносят и граждане, чей выбор абсолютно случаен. Эта группа избирателей в среднем дает равномерный вклад в доли голосов,получаемых кандидатами.
 При определении эмпирического закона распределения
При определении эмпирического закона распределения 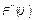 получается на каждом выделенном интервале
получается на каждом выделенном интервале 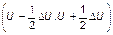 , где
, где 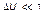 , путем усреднения по множеству эмпирических данных, соответствующему этому интервалу отклонений. И в этом смысле зависимость (1.4.12) является усредненной.
, путем усреднения по множеству эмпирических данных, соответствующему этому интервалу отклонений. И в этом смысле зависимость (1.4.12) является усредненной.
Не трудно видеть, что искажение закона голосования (т.е. его отклонения от 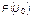 ) будет только в том случае, если распределение дополнительных вкладов голосов
) будет только в том случае, если распределение дополнительных вкладов голосов 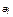 не будет гармоническим. В первом приближении можно записать
не будет гармоническим. В первом приближении можно записать
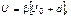 (1.4.48)
(1.4.48)
где 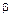 и
и 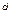 – параметры искажений.
– параметры искажений.
Используя выражение (1.4.48), можно, в принципе, восстановить невозмущенную эмпирическую функцию (закон) 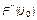 даже по искаженным вследствие нарушения условий гармоничности данным. Для этого в функции
даже по искаженным вследствие нарушения условий гармоничности данным. Для этого в функции 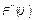 необходимо лишь произвести подстановку:
необходимо лишь произвести подстановку:
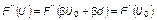 (1.4.49)
(1.4.49)
Полученный в результате этого преобразования закон 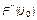 и должен сравниться с описанной выше теоретической функцией распределения отклонений отношений голосов
и должен сравниться с описанной выше теоретической функцией распределения отклонений отношений голосов
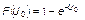
На основе результатов этого сравнения можно уже более или менее объективно судить о справедливости и несправедливости гармонического закона голосований, а более широко – об адекватности или неадекватности рассматриваемой статистической теории.
В случае положительного ответа на этот вопрос эмпирический закон 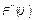 может быть использован для определения средних значений параметров
может быть использован для определения средних значений параметров 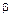 и
и 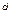 , наилучшим образом приближающих преобразованный эмпирический закон
, наилучшим образом приближающих преобразованный эмпирический закон 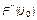 к закону
к закону 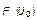 . При этом величины
. При этом величины 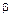 и
и 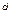 можно рассматривать в качестве показателей, характеризующих, в среднем, степень нарушения условий гармоничности.
можно рассматривать в качестве показателей, характеризующих, в среднем, степень нарушения условий гармоничности.
Для оценки адекватности статистической теории необходима предварительная оценка степени отклонения закона 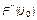 от закона
от закона 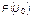 . Согласно приведенным исследованиям (рис. 1.4.12–1.4.14) максимальное отклонение значений функции
. Согласно приведенным исследованиям (рис. 1.4.12–1.4.14) максимальное отклонение значений функции 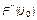 от значений функции
от значений функции 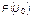 , как правило, не превосходит 20–30%. С учетом заведомого наличия в использованных эмпирических данных искажений, обусловленных нарушениями условиями гармоничности, этот результат следует рассматривать как подтверждение справедливости рассматриваемых модельных представлений.
, как правило, не превосходит 20–30%. С учетом заведомого наличия в использованных эмпирических данных искажений, обусловленных нарушениями условиями гармоничности, этот результат следует рассматривать как подтверждение справедливости рассматриваемых модельных представлений.
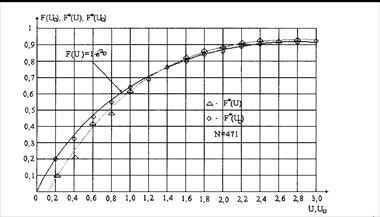
Рис. 1.4.14
В качестве интегральной характеристики степени расхождения законов 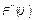 и
и 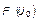 следует рассматривать величину
следует рассматривать величину
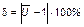 .
.
Результаты расчетов по более чем 500 данным показывают, что 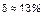 . Этот факт, очевидно, – еще одно убедительное подтверждение адекватности статистической теории голосований.
. Этот факт, очевидно, – еще одно убедительное подтверждение адекватности статистической теории голосований.
Опыт показывает, что в качестве оценки величины 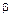 можно принять
можно принять 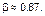 а в качестве оценки d –
а в качестве оценки d – 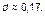
Используя полученные оценки, можно записать
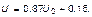
Результаты коррекции функции 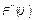 с помощью полученного выражения представлены на рис. 1.4.12. Как видно из него, расхождение между
с помощью полученного выражения представлены на рис. 1.4.12. Как видно из него, расхождение между 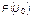 и
и 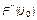 существенно снизилось. Весьма существенно улучшилась и оценка среднего значения величины
существенно снизилось. Весьма существенно улучшилась и оценка среднего значения величины 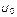 ; соответствующая погрешность стала равной
; соответствующая погрешность стала равной
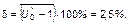
Отсюда следует, что если эмпирические данные преобразовать таким образом, чтобы исключить по-возможности влияние возмущающих факторов, обусловленных нарушениями условий гармоничности голосований, то при достаточно большой статистике гармонический закон голосований будет выполняться с весьма высокой точностью.
Заметим, однако, что приведенные оценки параметров искажений и смещений 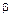 и d закона распределения отношений голосов соответствуют лишь в той выборке эмпирических данных, которая использовалась в данном исследовании. Для других исходных данных эти оценки могут оказаться совершенно другими. Например, для некоторых выборок, как показывает опыт, может даже поменяться знак параметра смещения d, а параметр искажения
и d закона распределения отношений голосов соответствуют лишь в той выборке эмпирических данных, которая использовалась в данном исследовании. Для других исходных данных эти оценки могут оказаться совершенно другими. Например, для некоторых выборок, как показывает опыт, может даже поменяться знак параметра смещения d, а параметр искажения 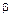 может оказаться больше единицы.
может оказаться больше единицы.
Параметры 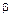 и d связаны с выборочным средним величины
и d связаны с выборочным средним величины 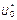 , которую легко найти, используя закон
, которую легко найти, используя закон 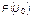 . Действительно,
. Действительно,
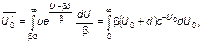
откуда
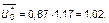
Таким образом, погрешность (искажение) среднего составляет 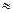 2%. Полученный результат достаточно хорошо согласуется с приведенной выше оценкой 2,5%, полученной непосредственно по статистическим данным, что еще раз убеждает нас в правильности выбранного подхода.
2%. Полученный результат достаточно хорошо согласуется с приведенной выше оценкой 2,5%, полученной непосредственно по статистическим данным, что еще раз убеждает нас в правильности выбранного подхода.
Мы уже говорили, что величина отклонения 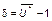 зависит от конкретной ситуации, сложившейся на момент данного голосования. Так, например, если по выборке из 391 данного, не включающей сведения, помимо прочего, о выборах 17.12.95 г. в России, величина
зависит от конкретной ситуации, сложившейся на момент данного голосования. Так, например, если по выборке из 391 данного, не включающей сведения, помимо прочего, о выборах 17.12.95 г. в России, величина
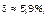
то по выборке из 108 данных, соответствующей именно этим выборам,
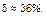
Объединенная выборка объема 526 дает для величины 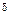 оценку, которая приводилась ранее:
оценку, которая приводилась ранее:
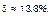
Из сказанного следует, что выборы 17.12.95 г. сопровождались очень серьезными нарушениями условий гармоничности. Но еще более значительные искажения характерны для президентских выборов 1996 г. в России.
 ?
?
Вопросы и упражнения
1. Дайте определение понятия информации.
2. Обсудите проблемы эволюции системы языков. Поясните основные идеи модели большого энергоинформационного взрыва. В чем состоит проблема глобализации?
3. Дайте определение основных фундаментальных свойств информации.
4. Предполагая равновероятность появления символов алфавита, на любой позиции сообщения с помощью формулы Шеннона подсчитайте общее количество информации в следующем сообщении:

 «Гу ернатор посетил ю ные районы области».
«Гу ернатор посетил ю ные районы области».
5. Охарактеризуйте основные семантические свойства информации. Поясните, как можно подсчитать объем семантической информации; что такое истинность информации?
6. Обсудите понятие ассоциативной семантической информации. От чего зависит ее объем?
7. Охарактеризуйте основные прагматические свойства информации.
8. Поясните роль законов интерпретации, поясните взаимосвязь законов интерпретации с возможностью управления индивидуальным и общественным сознанием.
9. Обсудите основные результаты статистической теории голосований и возможности ее применения для анализа качества выборных кампаний.

структуризация
социально-политических
и экономических
систем
 2.1
2.1
Дата добавления: 2016-12-08; просмотров: 1106;
