Понятие отношения на множестве
Чтобы определить общее понятие бинарного отношения на множестве, поступим так же, как и в случае с соответствиями, т.е. рассмотрим сначала конкретный пример. Пусть на множестве X = {2, 4, 6, 8} задано отношение «меньше». Это означает, что для любых двух чисел из множества X можно сказать, какое из них меньше: 2 < 4, 2 < 6, 2 < 8, 4 < 6, 4 < 8, 6 < 8. Полученные неравенства можно записать иначе, в виде упорядоченных пар: (2, 4), (2, 6), (2, 8), (4, 6), (4, 8), (6, 8). Но все эти пары есть элементы декартова произведения Х х Х, поэтому об отношении «меньше», заданном на множестве X, можно сказать, что оно является подмножеством множества Х х X.
Вообще бинарные отношения на множестве X определяют следующим способом:
Определение. Бинарным отношением на множестве X называется всякое подмножество декартова произведения Х х Х.
Так как в дальнейшем мы будем рассматривать только бинарные отношения, то слово «бинарные», как правило, будем опускать.
Условимся отношения обозначать буквами R, S, T, P и др.
Если R - отношения на множестве X, то, согласно определению, R с X х X. С другой стороны, если задано некоторое подмножество множества X х X, то оно определяет на множестве X некоторое отношение R.
Утверждение о том, что элементы х и у находятся в отношении R, можно записывать так: (х, у) € R или хRу. Последняя запись читается: «Элемент х находится в отношении R с элементом у».
Отношения задают так же, как соответствия. Отношение можно задать, перечислив пары элементов множества X, находящиеся в этом отношении. Формы представления таких пар могут быть различными - они аналогичны формам задания соответствий. Отличия касаются задания отношений при помощи графа.
Построим, например, граф отношений «меньше», заданного на множестве X = {2, 4, 6, 8}. Для этого элементы множества X изобразим точками (их называют вершинами графа), а отношение «меньше» — стрелкой (рис. 93).
На том же множестве X можно рассмотреть другое отношение — «кратно». Граф этого отношения будет в каждой вершине иметь петлю (стрелку, начало и конец которой совпадают), так как каждое число кратно самому себе (рис. 94). Отношение можно задать при помощи предложения с двумя переменными. Так, например, заданы рассмотренные выше отношения «меньше» и «кратно», причем использована краткая форма предложений «число x меньше числа у» и «число х кратно числу у». Некоторые такие предложения можно записывать, используя символы. Например, отношения «меньше» и «кратно» можно было задать в таком виде: «x < у», «х : у». Отношение «х больше у на 3» можно записать в виде равенства х = у + 3 (или x - у = 3).
Для отношения R, заданного на множестве X, всегда можно задать отношение R-1, ему обратное, - оно определяется так же, как соответствие, обратное данному. Например, если R - отношение «х меньше y», то обратным ему будет отношение «у больше x».
Понятием отношения, обратного данному, часто пользуются при начальном обучении математике. Например, чтобы предупредить ошибку в выборе действия, с помощью которого решается задача: «У Пети 7 карандашей, что на 2 меньше, чем у Бори. Сколько карандашей у Бори?» - ее переформулируют: «У Пети 7 карандашей, а у Бори на 2 больше. Сколько карандашей у Бори?» Видим, что переформулировка свелась к замене отношения «меньше на 2» обратным ему отношением «больше на 2».
Упражнения
1.Приведите примеры отношений, существующих между:
а) натуральными числами;
б) прямыми на плоскости;
в) треугольниками;
г) множествами.
2.На множестве X = {0, 3, 6, 9, 12, 15, 18} задано отношение R. Перечислите пары чисел, связанных этим отношением и постройте его граф, если:
а) R - «x- больше у в 3 раза»;
б) R - «x больше у на 3».
3. Запишите в виде равенства предложение:
а) Число x меньше у на 2.
б) Число x меньше у в 2 раза.
4. Задает ли на множестве X = {2, 4, 6, 8} какое-либо отношение следующее множество упорядоченных пар:
а) {(2,2), (4,4), (6, 6), (8, 8)}; б) {(4, 2), (6, 4), (8, 6), (2, 1)}?
5. На множестве X = {2,4, 6, 8} рассматриваются отношения «х = у», «х : у» и «х больше у на 2». Какое из приведенных ниже подмножеств множества Х х Х задает данные отношения:
а) {(4,2), (6, 2), (8, 2), (6,4), (8, 4), (8, 6), (2,2), (4, 4), (6, 6), (8, 8)};
б) {(4,2), (6,4), (8,6)};
в) {(2,2), (4,4), (6,6), (8, 8)}.
6.Отношение «x ≥ y»рассматривается на множестве Х. Каким будет его график на координатной плоскости, если:
а) X ={2,4, 6, 8};
б) Х – множество натуральных чисел;
|
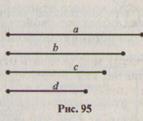
в) Х – множество действительных чисел?
7. На множестве отрезков (рис.95) задано отношение Р: «отрезок х длиннее отрезка у». Постройте граф этого отношения и задайте различными способами отношение, обратное данному.
8. Отношение S на множестве действительных чисел задано при помощи графика (рис. 96). Постройте график отношения, обратного данному.
9.Семья Волковых состоит из отца Михаила Петровича, матери Веры Ивановны и детей: Толи, Кати, Андрея и Оли. Между членами семьи существуют различные отношения родства: «быть матерью»; «быть дочерью»; «быть братом» и другие. Постройте графы указанных отношений и назовите другие, которые существуют между членами семьи Волковых. Есть ли среди них взаимно обратные?
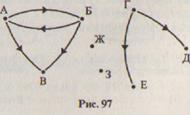
10. На рисунке 97 дан граф отношения «быть братом» на множестве детей, живущих в одном доме (дети обозначены точками А, Б, В, Г, Д, Е, Ж, З). Кто из них является девочкой, а кто мальчиком?
11.Решите арифметическим методом задачу, предварительно выделив все отношения, которые в ней рассматриваются:
а) На одной полке было в 3 раза больше книг, чем на другой. Когда с первой полки сняли 8 книг, а на другую положили 5 книг, то на второй полке стало на 17 книг меньше, чем на первой. Сколько книг было на каждой полке?
б) На автобазе было на 46 грузовых машин больше, чем автобусов. Сколько грузовых машин было на автобазе, если их было в 3 раза больше, чем автобусов?
Дата добавления: 2016-05-11; просмотров: 4515;