Схемы дедуктивных умозаключений.

Рассмотрим подробнее дедуктивные (правильные) умозаключения. Согласно определению (п. 25), в дедуктивном умозаключении посылки и заключение находятся в отношении логического следования. Это означает, что в нем всегда из истинных посылок следует истинное заключение. Но как строить такие умозаключения и проверять их правильность?

В логике считают, что правильность умозаключения определяется его формой и не зависит от конкретного содержания входящих в него утверждений. И в логике предлагаются такие правила, соблюдая которые, можно строить дедуктивные умозаключения. Эти правила называют правилами вывода или схемами дедуктивных (правильных) умозаключений. Правил много, но наиболее часто используются следующие:

А(х) ⇒ В(х), А(а) - правило заключения

В(а)

А(х) ⇒ В(х), В(а) - правило отрицания

А(а)

А(х) ⇒ В(х), В(х) ⇒ С(х) - правило силлогизма.

А(х) ⇒ С(х)

Выясним, что обозначают все знаки, использованные в записи этих правил; как их применять на практике.

Рассмотрим, например, правило заключения. В нем обозначено две посылки А(х) ⇒ В(х) и А(а). Первую называют общей посылкой, это может быть теорема, определение и, вообще, предложение вида А(х) ⇒ В(х). Вторую посылку А(а) называют частной, она получается из условия А(х) при х = а. Предложение В(а) – это заключение, оно получается из В(х) при х = а. Посылки отделены от заключения чертой, которая заменяет слово «следовательно».

Приведем пример умозаключения, выполненного по правилу заключения:

Если запись числа х оканчивается цифрой 5, то число х делится на 5. Запись числа 135 оканчивается цифрой 5. Следовательно, число 135 делится на 5.

В качестве общей посылки в этом умозаключении выступает утверждение вида «если А(х), то В(х), где А(х) – это «запись числа х оканчивается цифрой 5», а В(х) – «число х делится на 5». Частная посылка представляет собой высказывание, которое получилось из условия общей посылки при х = 135 (т.е. это А(135)). Заключение является высказыванием, полученным из В(х) при х = 135 (т.е. это В(135)).

Приведем теперь пример умозаключения, выполненного по правилу отрицания:

Если запись числа х оканчивается цифрой 5, то число х делится на 5. Число 177 не делится на 5. Следовательно, оно не оканчивается цифрой 5.

Видим, что в этом умозаключении общая посылка такая же, как и в предыдущем, а частная представляет собой отрицание высказывания «число 177 делится на 5» (т.е. это неверно, что В(177)). Заключение – это отрицание предложения «Запись числа 177 не оканчивается цифрой 5» (т.е. неверно, что А(177)).

И наконец, рассмотрим пример умозаключения, построенного по правилу силлогизма.

Если число х кратно 12, то оно кратно 6. Если число х кратно 6, то оно кратно 3. Следовательно, если число х кратно 12, то оно кратно 3.

В этом умозаключении две посылки вида «если А(х), то В(х)» и «если В(х), то С(х)», где А(х) – это предложение «х кратно 12», В(х) – предложение «х кратно 6» и С(х) – предложение «х кратно 3». Заключение представляет собой высказывание «если А(х), то С(х)».

Конечно, возникает вопрос, почему умозаключения, выполнены по правилам заключения, отрицания и силлогизма, будут дедуктивными (правильными)? Дело в том, что, выполняя рассуждения по этим правилам, мы всегда будем получать истинное заключение, что и требовалось в дедуктивном умозаключении. Убедиться в этом можно, если воспользоваться кругами Эйлера.

В логике существуют различные способы проверки правильности умозаключений. Рассмотрим тот, который предполагает использование кругов Эйлера. Сначала данное умозаключение можно записать на теоретико-множественном языке, затем посылки изобразить на кругах Эйлера, считая их истинными. После этого надо выяснить, всегда ли при таких посылках истинно заключение. Если оказывается, что всегда, то говорят, что данное умозаключение правильное, дедуктивное. Если же возможен рисунок, из которого видно, что заключение может быть ложным, то говорят, что всякое умозаключение, выполненное по такой схеме, является недедуктивным, неправильным.

Покажем, что умозаключение, выполненное по правилу заключения, является дедуктивным. Сначала запишем это правило на теоретико-множественное языке.

Посылка А(х) ⇒ В(х) может быть записана в виде ТА ⊂ ТВ, где ТА и ТВ – множества истинности высказывательных форм А(х) и В(х).

Частная посылка А(а) означает, что а ∈ ТА, а заключение В(а) показывает, что а ∈ ТВ. Все умозаключение, построенное по правилу заключения, запишется на теоретико-множественном языке так:

ТА ⊂ ТВ, а ∈ ТА .

а ∈ ТВ

Изобразив на кругах Эйлера множества ТА и ТВ, мы увидим, что а ∈ ТА ⇒ а ∈ ТВ.

ТВ

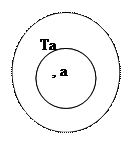
Аналогичным образом можно проверить и другие правила дедуктивных умозаключений. Кроме того, такой способ проверки правильности умозаключений можно использовать и в тех случаях, когда умозаключение выполнено по схеме, отличной от рассмотренных.

Задача. Правильно ли следующее умозаключение: «если запись числа оканчивается цифрой 5, то число делится на 5. Число 125 делится на 5. Следовательно, запись числа 125 оканчивается цифрой 5».

Ответ: заключение может быть истинным, а само умозаключение не быть дедуктивным, правильным.