Полуцикловые неразрывные характеристики

В условиях эксплуатации нагрузки не всегда достигают значений, при которых происходит разрушение материала. В этой связи проводится оценка поведения материалов под нагрузками, меньшими предельных, при которых материалы разрушаются, и оцениваются:

а) усилие Р в пробе при растяжении на заданную величину L за определенное время τ , что характеризует жесткость материала (способность сопротивляться деформированию);

б) удлинение L под действием заданной величины нагрузки Р в течение определенного времени τ, что характеризует растяжимость материала (способность изменять размеры при приложении нагрузки).

Основными характеристиками жесткости текстильных материаловявляются

Модуль продольной упругости (модуль 1го рода) 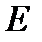, который оценивается как отношение 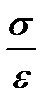на участке диаграммы, где зависимость 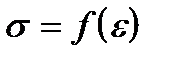имеет линейный характер.

В экспериментах обычно определяется при 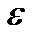= 1 %,

т.е. по в начальной стадии деформирования (когда

проявляется в основном упругая составляющая

полной деформации.

Рис. 14 Общий вид диаграммы

(Примечание: Выражение закона Гука имеет вид 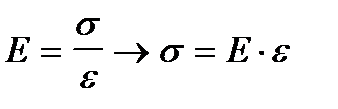, где 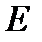- модуль Юнга.

Модуль начальной жесткости( 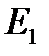) характеризует способность материалов сопротивляться деформированию в начальной фазе процесса; соответствует напряжению в пробе при 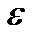= 1 %; близок к модулю продольной упругости Е (модулю Юнга); может быть рассчитан по формуле:

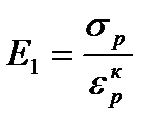, (41)

где 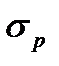- разрывное напряжение, Па;

- относительное разрывное удлинение;

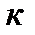- характеристика диаграммы растяжения, определяемая по формуле ,

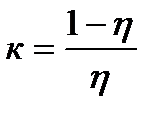где 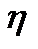- коэффициент полноты диаграммы растяжения.

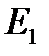характеризует сопротивление деформированию малорастяжимых материалов, например, тканей.

Модуль текущей жесткостиЕт.ж. используется для оценки жесткости материалов при любой величине деформации. Рассчитывается как 1-ая производная от σ = 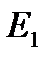по формуле:

(42)

Модуль текущей конечной жесткости 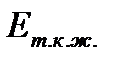- характеристика жесткости пробы в момент разрушения

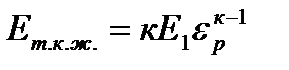(43)