Закон розподілу та числові характеристики функції немонотонного неперервного випадкового аргументу
Нехай  неперервна випадкова величина із щільністю розподілу ймовірностей
неперервна випадкова величина із щільністю розподілу ймовірностей  і випадкова величина
і випадкова величина 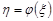 . Нехай функція
. Нехай функція  неперервна, кусково-монотонно диференційовна функція на області визначення, тоді кожна її монотонна частина має свою обернену функцію
неперервна, кусково-монотонно диференційовна функція на області визначення, тоді кожна її монотонна частина має свою обернену функцію 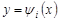 , і=1,2,...., n, де п – число монотонних частин функції
, і=1,2,...., n, де п – число монотонних частин функції  . У цьому випадку щільність розподілу випадкової величини
. У цьому випадку щільність розподілу випадкової величини 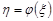 знаходиться за формулою:
знаходиться за формулою:
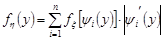 . (20.6)
. (20.6)
Дійсно, припустимо, що графіком функції  буде крива представлена на рис. 20.4.
буде крива представлена на рис. 20.4.
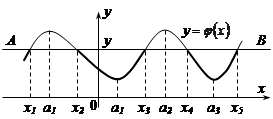 |
Рис.20.4.
Розділимо область визначення функції  на монотонні частини. На рис. 20.4 такими частинами будуть інтервали
на монотонні частини. На рис. 20.4 такими частинами будуть інтервали  ,
, 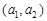 ,
, 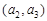 ,
, 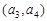 ,
,  . В кожній з цих частин існує обернена монотонна функція
. В кожній з цих частин існує обернена монотонна функція 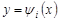 , і=1,2,... 5. Розглянемо подію
, і=1,2,... 5. Розглянемо подію 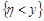 . Ця подія відбудеться, якщо випадкова точка
. Ця подія відбудеться, якщо випадкова точка 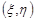 попаде на ту частину кривої
попаде на ту частину кривої  , що розташована нижче прямої
, що розташована нижче прямої 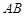 . Таким чином, подія
. Таким чином, подія 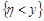 рівносильна об’єднанню несумісних подій
рівносильна об’єднанню несумісних подій 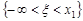 ,
, 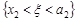 ,
, 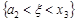 ,
, 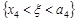 ,
, 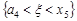 . Отже,
. Отже,
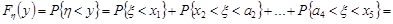
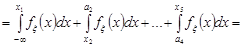
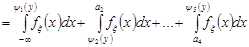 .
.
Диференціюємо останню рівність по  , використовуючи формулу (20.3), маємо
, використовуючи формулу (20.3), маємо
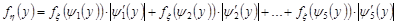 .
.
У загальному випадку маємо формулу (20.6).
Для знаходження числових характеристик випадкової величини 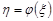 використовуємо формули аналогічні формулам (20.4) та (20.5).
використовуємо формули аналогічні формулам (20.4) та (20.5).
Приклад 20.8. Випадкова величина 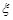 має рівномірний розподіл в інтервалі
має рівномірний розподіл в інтервалі 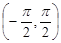 . Знайти закон розподілу випадкової величини
. Знайти закон розподілу випадкової величини 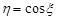 .
.
Розв’язання. Функція 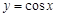 – немонотонна функція в інтервалі
– немонотонна функція в інтервалі 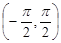 . У цьому інтервалі вона складається з двох монотонних частин. Отже, при
. У цьому інтервалі вона складається з двох монотонних частин. Отже, при 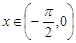
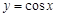 має обернену функцію
має обернену функцію 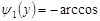 y, при
y, при 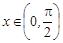 оберненою функцією буде
оберненою функцією буде 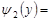
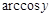 .З умови задачі щільність розподілу випадкової величини
.З умови задачі щільність розподілу випадкової величини 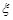 дорівнює:
дорівнює:
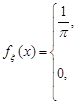

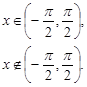
За формулою (20.6) знаходимо:
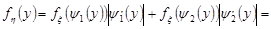
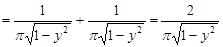 ,
, 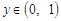 .
.
Приклад 20.9. Випадкова величина 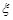 розподілена рівномірно на проміжку
розподілена рівномірно на проміжку 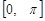 . Знайти числові характеристики випадкової величини
. Знайти числові характеристики випадкової величини 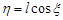 .
.
Розв’язання. Числові характеристики випадкової величини 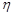 знайдемо за формулами (20.4) і (20.5)
знайдемо за формулами (20.4) і (20.5)
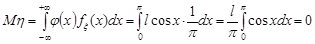 ;
;
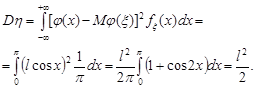
Дата добавления: 2016-11-02; просмотров: 516;
