Закон розподілу та числові характеристики функції дискретного випадкового аргументу

При розв’язанні багатьох імовірнісних задач виникає необхідність визначення закону розподілу та числові характеристики детермінованої функції випадкового чи випадкових аргументів за законом розподілу аргументів. Розглянемо, перш за все, найпростіший випадок цієї задачі.

Нехай 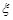– дискретна випадкова величина, закон розподілу якої має вигляд: 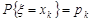, k = 1, 2,..., тоді закон розподілу дискретної випадкової величини 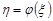знаходимо за таким алгоритмом:

1) обчислюємо всі значення, які може набувати випадкова величина 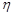, тобто 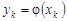, k = 1, 2, ... ;

2) упорядковуємо ці значення;

3) під упорядкованими значеннями 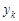пишемо відповідні ймовірності, якщо 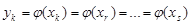, то ймовірність обчислюємо так:

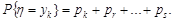
Для визначення числових характеристик функцій одного дискретного випадкового аргументу достатньо знайти тільки закон розподілу аргументу. Доведемо наступну теорему.

Теорема 20.1. Якщо дискретна випадкова величина 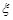має розподіл 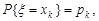k=1, 2,..., то числові характеристики випадкової величини 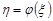обчислюють за формулами:

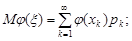(20.1)

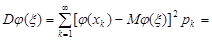
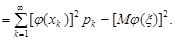(20.2)

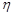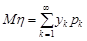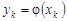Доведення. Доведемо тільки формулу (20.1). Математичне сподівання випадкової величини за означенням знаходять за формулою , де , k = 1, 2, ..., тобто значення, які набуває випадкова величина 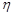. Імовірності, з якими ці значення набуваються, дорівнюють 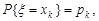k=1, 2,... . Отже, маємо формулу (20.1).

Таким чином, якщо з умови задачі необхідно знайти тільки числові характеристики функцій одного дискретного випадкового аргументу, то знаходити сам закон розподілу функції необов’язково.

Приклад 20.1. Закон розподілу дискретної випадкової величини 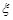заданий рядом розподілу (табл.20.1).

Таблиця 20.1

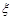
	–2	–1	–1/2	1/2
р	1/4	1/12	1/9	2/9	1/6	1/6

Знайти закон розподілу випадкової величини .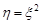

Розв’язання. Спочатку знайдемо значення, які набуває випадкова величина :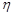

.

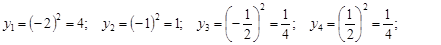
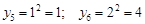Знайдемо ймовірності, з якими ці значення набуваються:

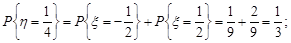
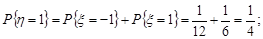
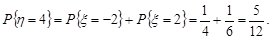
Отже, ряд розподілу випадкової величини 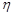має вигляд (табл.20.2).

Таблиця 20.2

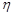
	1/4
р	1/3	1/4	5/12

Приклад 20.2. Знайти числові характеристики функції 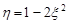, якщо 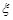– дискретна випадкова величина, яка задана рядом розподілу (табл. 20.3).

Таблиця 20.3

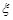
р	0,2	0,5	0,3

Розв’язання. Закон розподілу дискретної випадкової величини 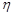не знаходимо. Одразу за формулою (20.1) обчислюємо математичне сподівання :

.

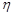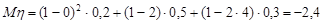Дисперсію випадкової величини 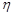знайдемо за формулою (20.2):

.

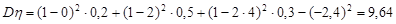Приклад 20.3. Проводять незалежні випробування, в кожному з яких подія А відбувається з імовірністю p. Випробування закінчують після того, як відбулася подія А. Загальна кількість випробувань не повинна перевищувати число N. Знайти математичне сподівання кількості випробувань .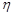

Розв’язання. Введемо випадкову величину 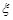– кількість проведених випробувань. Якщо вважати, що обмеження на кількість випробувань нема, то випадкова величина 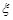має геометричний розподіл із параметром p. Випадкову величину 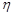, з урахуванням обмеження на кількість випробувань, можна записати так: 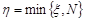. Оскільки величина 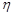є функцією випадкового аргументу 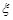, то для знаходження математичного сподівання 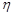використаємо формулу (20.1).

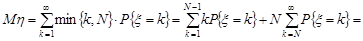
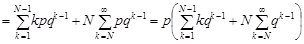, де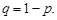

Перша сума цього виразу дорівнює

.

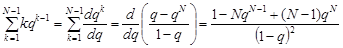Друга сума 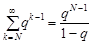. Отже, математичне сподівання випадкової величини 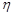дорівнює

.

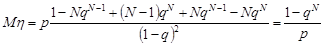20.2. Закон розподілу та числові характеристики функції монотонного неперервного випадкового аргументу

Нехай неперервна випадкова величина із щільністю розподілу ймовірностей і випадкова величина 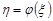. Припустимо, що детермінована функція 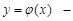неперервна, монотонна, диференційовна на області визначення, тоді вона має обернену диференційовну функцію 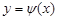. Знайдемо у цьому випадку закон розподілу неперервної випадкової величини .

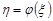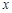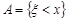Для будь-яких дійсних значень та розглянемо події та 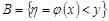. Якщо функція 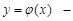неперервна, монотонно зростаюча функція, то ці події рівносильні 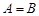, оскільки випадкова точка 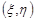попадає на ту частину графіка функції 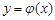, котра лежить нижче прямої 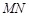(рис.20.1) та зліва від точки з абсцисою .

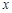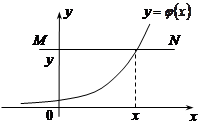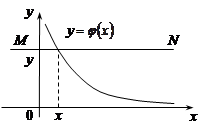Рис.20.1. Рис.20.2.

Враховуючи сказане, функція розподілу випадкової величини 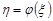буде такою:

.

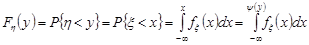Зокрема, якщо область можливих значень випадкової величини 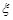є скінчений проміжок 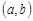, то функція розподілу величини 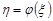має вигляд

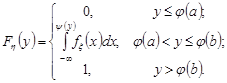
Знайдемо щільність розподілу 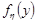, як похідну від функції розподілу:

.

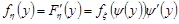Якщо функція 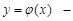неперервна, монотонно спадна функція, то рівносильними будуть події 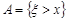та 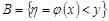(Рис 20.2). У такому випадку

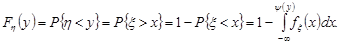
Щільність розподілу випадкової величини 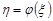дорівнює

.

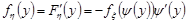Згадаємо, що похідна монотонно зростаючої функції – додатна, а монотонно спадної функції – від’ємна і тому щільність розподілу функції монотонного неперервного випадкового аргументу можна записати однією формулою

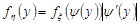(20.3)

Якщо неперервна випадкова величина 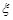має щільність розподілу ймовірностей 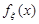, то числові характеристики випадкової величини 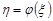обчислюємо так:

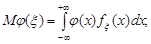(20.4)

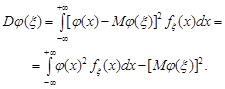(20.5)

Отже, як і у випадку дискретного випадкового аргументу, для знаходження числових характеристик функцій одного неперервного випадкового аргументу необов’язково знаходити сам закон розподілу функції.

Доведемо, наприклад, формулу (20.4). Нехай функція 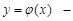неперервна, монотонно зростаюча функція. За означенням і формулою (20.3)

.

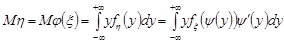Врахуємо, що 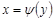, 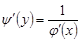і 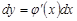, тоді

.

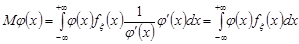Для монотонно спадної функції 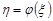обернена функція 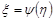буде також монотонно спадною, тому

,

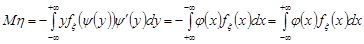отже, формула (20.4) також справедлива.

Аналогічно можна довести формулу (20.5).

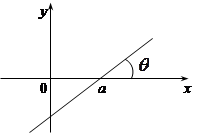Приклад 20.4. Через точку з координатами (a, 0), а > 0 на площині XOY навмання проведена пряма під гострим кутом 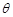до осі ОХ (рис.20.3).

Рис.20.3.

Значення кута 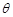мають рівномірний розподіл в інтервалі 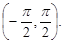Знайти закон розподілу ординати точки перетину прямої з віссю OY.

Розв’язання. Випадкова величина 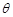за умовою задачі має рівномірний розподіл в інтервалі 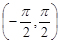, тому щільність розподілу ймовірностей випадкової величини 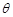буде такою:

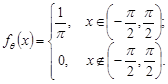
Ордината точки перетину прямої з віссю 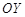є випадковою величиною 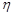, яка зв’язана з кутом 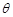формулою 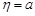tg 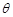. Функція 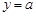tgx, 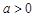є зростаюча диференційовна функція в інтервалі 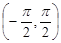. Вона має обернену функцію 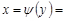arctg 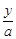. Відомо, що похідна 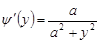. Отже, за формулою (20.3) знаходимо:

, .

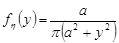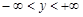Це є щільність розподілу ймовірностей для закону Коші.

Приклад 20.5. Випадкова величина 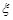розподілена за канонічним нормальним законом. Знайти закон розподілу випадкової величини .

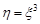Розв’язання. Щільність розподілу канонічної гаусівської величини 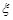має вигляд 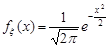. За формулою (20.3)

.

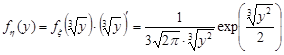Приклад 20.6. Випадкова напруга 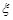, яку подано на вхід стабілізатора, розподілена нормально з параметрами 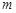та 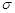. Стабілізатор залишає напругу рівною 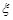, якщо 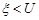і робить її рівною 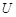, якщо 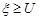, тобто працює за правилом 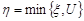. Знайти математичне сподівання випадкової величини 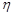– напруги на виході стабілізатора.

Розв’язання. За формулою (20.4) маємо

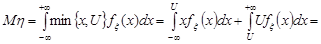
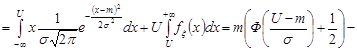
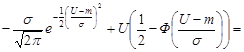
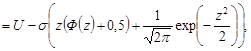де .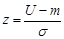

Приклад 20.7. Нехай 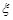– довільна випадкова величина із функцією розподілу 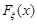. Знайти закон розподілу випадкової величини .

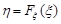Розв’язання. Розглянемо випадкову величину 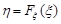. Знайдемо її функцію розподілу 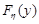. Відомо, що функція 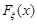є монотонно неспадною. Тоді

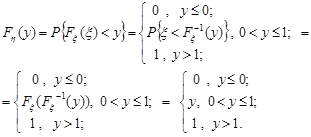
Отже,

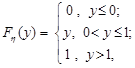
тобто незалежно від закону розподілу випадкової величини 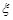, випадкова величина 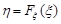має рівномірний розподіл на проміжку [0,1].

Результат цієї задачі використовується на практиці для отримання випадкової величини з заданим законом розподілу.

Є програми, які генерують випадкову величину рівномірно розподілену на проміжку [0,1]. Треба отримати випадкову величину 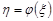з наперед заданою функцією розподілу 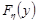. Із розв’язаного прикладу 20.7 випливає, що в якості функції розподілу випадкової величини 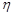треба взяти функцію 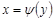– обернену до функції .