Вторичные параметры однородной линии

Определим соотношение между падающими и отраженными волнами в конце линии, т.е. при x = l. Значения напряжения и тока в конце линии равны напряжению и току нагрузки: Ú_x=l = Ú_Н, Ì_x=l = Ì_Н.

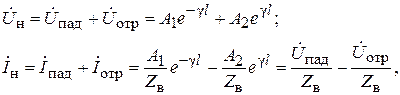(6.19)

где на основании выражений (6.9 и 6.10)

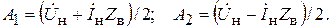(6.20)

Учитывая, что Ú_Н = Ì_НZ_Н равенства (6.19) можно переписать в виде:

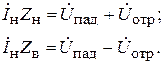
Складывая эти равенства и вычитая из первого второе, имеем:

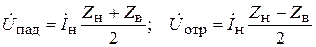. (6.21)

Коэффициент отражения. Соотношение между амплитудами отраженной и падающей волнами напряжения или тока можно оценить коэффициентом отражения по напряжению

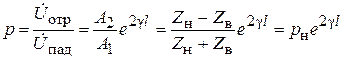, (6.22)

где 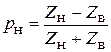- коэффициент отражения в конце линии (в нагрузке). (6.23)

Отсюда .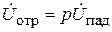

Коэффициент отражения по напряжению показывает, какую часть амплитуды падающей волны в конце линии составляет амплитуда отраженной волны.

Рассмотрим некоторые частные режимы работы линии.

1. Если сопротивление нагрузки равно волновому сопротивлению Z_Н =Z_В, то коэффициент отражения равен нулю – p = 0. Это значит, что отраженной волны нет Ú_{н отр} = 0 и вся энергия падающей волны выделяется в нагрузке.

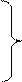
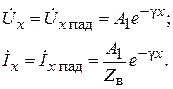(6.24)

Этот ражим называется режимом бегущих волн и характеризует согласование линии с нагрузкой.

2. Если линия замкнута накоротко на конце (короткое замыкание Z_Н = 0), то коэффициент p_н = –1. Падающая и отраженная волны напряжения в конце линии имеют равные амплитуды и сдвинуты по отношению друг к другу по фазе на 180^о т. е. Ú_{н пад} = –Ú_{н отр}. Амплитуда результирующей волны напряжения в конце линии будет равна нулю.

При холостом ходе в конце линии Z_Н = ∞ коэффициент p_н = 1. Падающая и отраженная волны напряжения в конце линии равны по амплитуде и совпадают по фазе, а результирующее напряжение увеличивается вдвое.

Режим волн, при котором коэффициент │p│ = 1, называется режимом стоячих волн.

3. Если │Z_Н│≠│Z_В│, коэффициент │p│< 1, т.е. в линии прямая волна частично отражается от нагрузки. Этот режим называется режимом смешанных волн.

Волновое сопротивление. Из выражений (6.18) следует, что амплитуды падающей волны напряжения и тока связаны между собой коэффициентом пропорциональности Z_B, называемым волновым сопротивлением

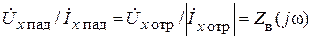. (6.25)

Волновое сопротивление можно рассчитать по погонным параметрам (6.7)

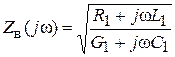. (6.26)

Коэффициент распространения. Коэффициент распространения введен формулой (6.12)

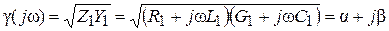(6.27)

В режиме согласованного включения линии из (6.22) напряжение и ток в любой точке x линии и на входе линии при x = 0 равны соответственно

.

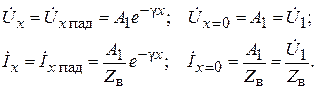Отношение этих напряжений и токов равно

.

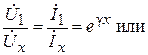
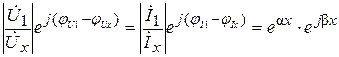Отсюда

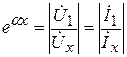и βx = φ_u1 – φ_ux = φ_i1 – φ_ix.

Для отрезка линии единичной длины ( 1 км, 1 м и т. д.) можно записать:

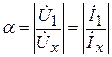; β = φ_u1 – φ_ux = φ_i1 – φ_ix.

Вещественная часть коэффициента распространения α характеризует изменение напряжения и тока по абсолютной величине при распространении энергии на расстояние, равное единице длины линии. Она называется коэффициентом ослабления линии и измеряется в неперах, отнесенных к единице длины линии (в радиосвязи – Нп/м). При использовании десятичного логарифма вместо натурального

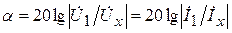
измеряется в дБ/м.

Мнимая часть коэффициента распространения β характеризуется изменением напряжения и тока по фазе. Она называется коэффициентом фазы линии и измеряется в рад/м. Вместо радиан могут использоваться градусы.