Задачи с несколькими выходными параметрами
Задачи с одним выходным параметром имеют очевидные преимущества. Но на практике чаще всего приходится учитывать несколько выходных параметров. Иногда их число довольно велико. Так, например, при производстве резиновых и пластмассовых изделий приходится учитывать физико-механические, технологические, экономические, художественно-эстетические и другие параметры (прочность, эластичность, относительное удлинение, способность смеси прилипать к форме и т. д.). Математические модели можно построить для каждого из параметров, но одновременно оптимизировать несколько функций невозможно.
Обычно оптимизируется одна функция, наиболее важная с точки зрения цели исследования, при ограничениях, налагаемых другими функциями. Поэтому из многих выходных параметров выбирается один в качестве параметра оптимизации, а остальные служат ограничениями. Всегда полезно исследовать возможность уменьшения числа выходных параметров. Для этого можно воспользоваться корреляционным анализом.
При этом между всевозможными парами параметров необходимо вычислить коэффициент парной корреляции, который является общепринятой в математической статистике характеристикой связи между двумя случайными величинами. Если обозначить один параметр через у1, а другой — через у2, и число опытов, в которых они будут измеряться, – через N, так, что i=1, 2, … , N, где i — текущий номер опыта, то коэффициент парной корреляции r вычисляется по формуле
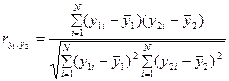
Здесь
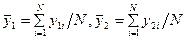
средние арифметические соответственно для у1 и у2.
Значения коэффициента парной корреляции могут лежать в пределах от -1 до +1. Если с ростом значения одного параметра возрастает значение другого, у коэффициента будет знак плюс, а если уменьшается, то минус. Чем ближе найденное значение 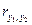 к единице, тем сильнее значение одного параметра зависит от того, какое значение принимает другой, т.е. между такими параметрами существует линейная связь, и при изучении процесса можно рассматривать только один из них. Необходимо помнить, что коэффициент парной корреляции как мера тесноты связи имеет четкий математический смысл только при линейной зависимости между параметрами и в случае нормального их распределения.
к единице, тем сильнее значение одного параметра зависит от того, какое значение принимает другой, т.е. между такими параметрами существует линейная связь, и при изучении процесса можно рассматривать только один из них. Необходимо помнить, что коэффициент парной корреляции как мера тесноты связи имеет четкий математический смысл только при линейной зависимости между параметрами и в случае нормального их распределения.
Для проверки значимости коэффициента парной корреляции нужно сравнить его значение с табличным (критическим) значением r, которое приведено в табл.1.1. Для пользования этой таблицей нужно знать число степеней свободы 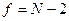 и выбрать определенный уровень значимости, например, равный 0,05. Такое значение уровня значимости называют еще 5%-ным уровнем риска, что соответствует вероятности верного ответа при проверке нашей гипотезы
и выбрать определенный уровень значимости, например, равный 0,05. Такое значение уровня значимости называют еще 5%-ным уровнем риска, что соответствует вероятности верного ответа при проверке нашей гипотезы 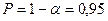 , или 95%. Это значит, что в среднем только в 5% случаев возможна ошибка при проверке гипотезы.
, или 95%. Это значит, что в среднем только в 5% случаев возможна ошибка при проверке гипотезы.
В практических исследованиях 5%-ный уровень риска применяется наиболее часто. Но экспериментатор всегда свободен в выборе уровня значимости, и возможны ситуации, в которых, например, требуется 1%-ный уровень риска. При этом возрастает надежность ответа. Проверка гипотезы сводится к сравнению абсолютной величины коэффициента парной корреляции с критическим значением. Если экспериментально найденное значение r меньше критического, то нет оснований считать, что имеется тесная линейная связь между параметрами, а если больше или равно, то гипотеза о корреляционной линейной связи не отвергается.
Таблица 1
Критические значения коэффициента парной корреляции при α= 0,05
| Число степеней свободы f | Критическое значение r | Число степеней свободы f | Критическое значение r | Число степеней свободы f | Критическое значение r |
| 0,997 | 0,602 | 0,456 | |||
| 0,950 | 0,576 | 0,444 | |||
| 0,878 | 0,553 | 0,433 | |||
| 0,811 | 0,532 | 0,423 | |||
| 0,754 | 0,514 | 0,349 | |||
| 0,707 | 0,497 | 0,273 | |||
| 0,666 | 0,482 | 0,217 | |||
| 0,632 | 0,468 | 0,195 |
При высокой значимости коэффициента корреляции любой из двух анализируемых параметров можно исключить из рассмотрения как не содержащий дополнительной информации об объекте исследования. Исключить можно тот параметр, который технически труднее измерять, или тот, физический смысл которого менее ясен. При планировании эксперимента целесообразно измерять все параметры, затем оценить корреляцию между ними и строить модели для их минимально возможного числа или же воспользоваться обобщенным параметром. Но бывают случаи, когда приходится рассматривать и коррелированные параметры.
Дата добавления: 2016-11-02; просмотров: 1530;
