Наносхеми на квантових автоматах

Для створення логічного інвертора на КА використовують чотири послідовно-паралельно розташовані лінії передачі (рис.6.4, а).

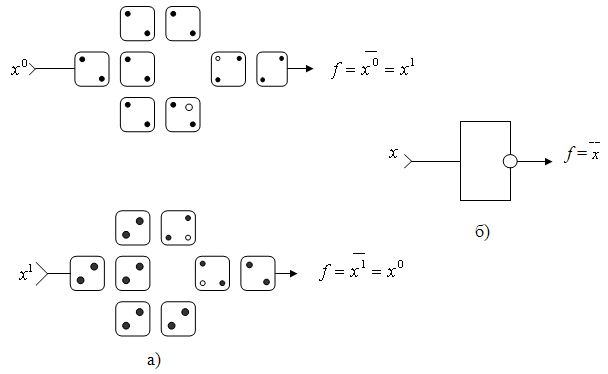
Рис.6.4. Наносхема виконання логічної операції заперечення НІ на КА (а) та умовне позначення інвертора (б)

Таке підключення КА забезпечує інверсію сигналу за рахунок кулонівського відштовхування електронів між кутовими квантовими точками автоматів у вихідних лініях схеми (рис.6.4, а). Таким чином, по дві квантові точки залишаються незаповненими.

Як і практично в усій наноелектроніці, найбільше застосування КА знаходять у схемах мажоритарного вибору. На рис.6.5 наведена повна електрична схема мажоритарного елемента (2 з 3) на базі дев’яти КА.

В центральній комірці (рис.6.5, а) під впливом електростатичної індукції, яку наводять оточуючі верхня, зліва та нижня сусідні комірки, формується діагональне розташування електронів, яке відповідає логічному нулю або одиниці за принципом вибору більшості. У подальшому цей логічний стан передається вправо через останню комірку на вихід схеми. Таким чином виконується логічна функція мажоритарного вибору (2 з 3):

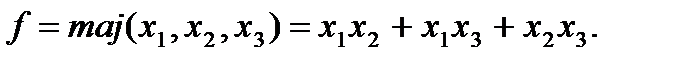(6.2)

Якщо на третьому вході МЕ (рис.6.5, б) постійно підтримувати логічний нуль чи одиницю, то схема в цілому здійснює логічні операції І чи АБО. В табл.6.1 наведені стани входів й виходу МЕ, розподіл надлишкових електронів у комірках спрощених схем МЕ, та умовні позначення елементів.

З табл.6.1 випливає, що реалізація мажоритарного елемента на квантових автоматах є однією з найпростіших з усіх розглянутих раніше (рис.5.2,б; 5.3,в; 5.4; 5.6,а та 5.14,а).

Для створення універсального МЕ (УМЕ) з прямим та інверсним виходами, електричну схему з табл.6.1 доповнюють схемою інвертора (рис.6.4,а). Логічна функція інверсного виходу описується рівнянням:

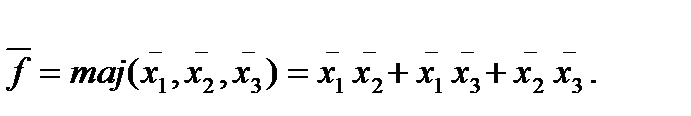(6.3)

Інколи функцію (6.3) називають мінорітарною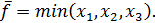

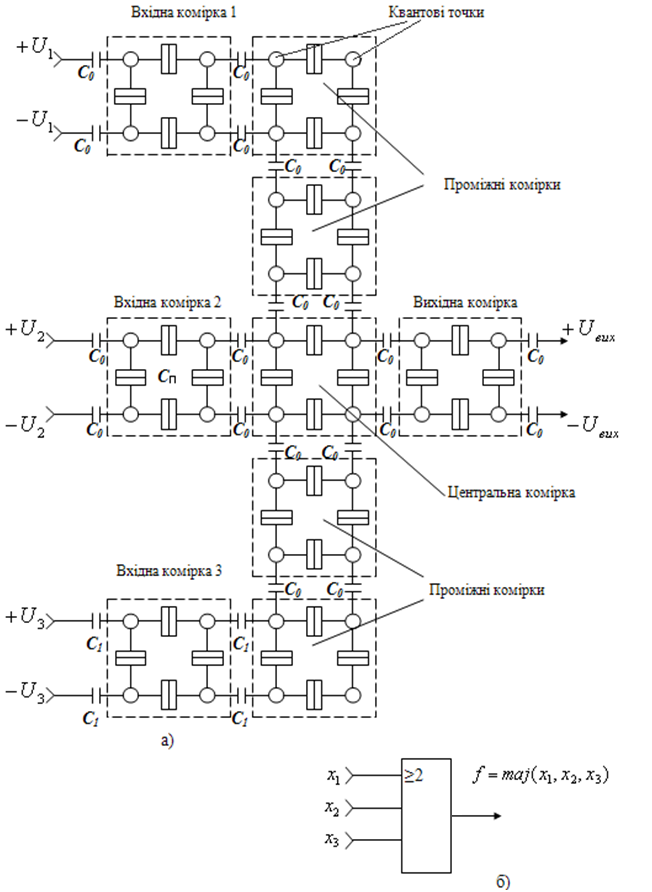
Рис.6.5. Електрична схема мажоритарного наноелемента (2 з 3) на квантових точках (а) та його умовне позначення (б)

Таблиця 6.1

Побудова логічних схем І та АБО з використанням мажоритарних елементів на квантових автоматах

Таблиця дійсності	Розподіл електронів в КА	Умовне позначення схем
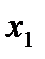
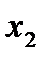
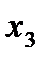
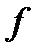
				x1=0 x2=0 f=0 x3=0	≥ 2 x1 f x2 x3 = 0     & x1 f= x1 x2 x2
				x1=0 x2=1 f=0 x3=0
				x1=1 x2=0 f=0 x3=0
				x1=1 x2=1 f=1 x3=0
				x1=0 x2=0 f=0 x3=1	≥2 x1 f x2   x3=1   f= x1+x2 x1 x2
				x1=0 x2=1 f=1 x3=1
				x1=1 x2=0 f=1 x3=1
				x1=1 x2=1 f=1 x3=1

На рис.6.6 показані схеми УМЕ на КА (а) і також логічних елементів, які здійснюють операції 2І-НІ (б) та 2АБО-НІ (в).

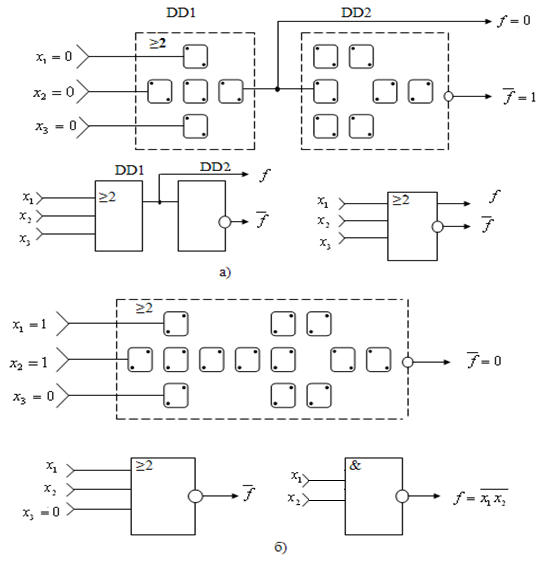
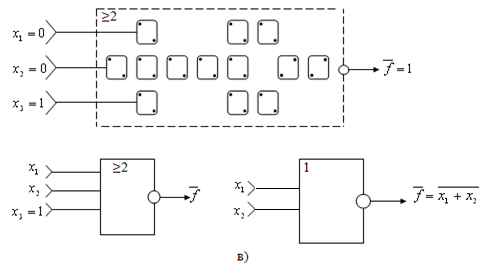
Рис.6.6. Реалізації схем універсального мажоритарного елемента на квантових автоматах (а), 2І-НІ (б) та 2АБО-НІ (в)

На рис.6.7 приведена схемна реалізація однорозрядного суматора з переносом у старший розряд на КА. Логічні рівняння цієї наносхеми:

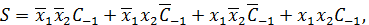(6.4)

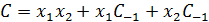. (6.5)

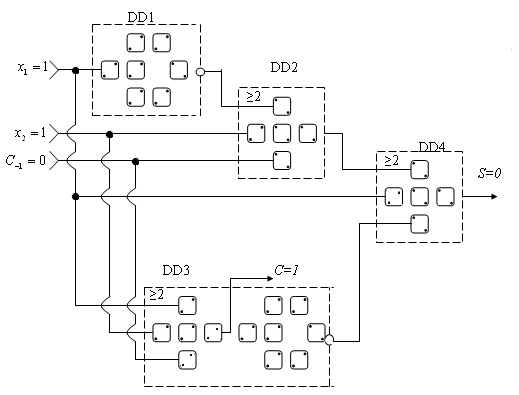
в)

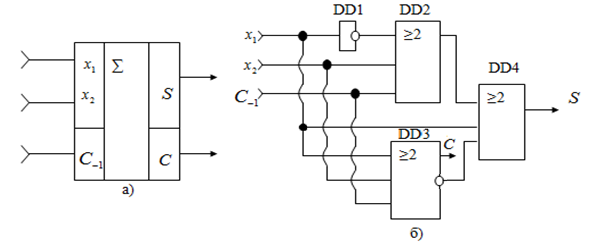
Рис.6.7. Однорозрядний наносуматор: умовне позначення (а), схемні реалізації на логічних елементах (б) та на квантових автоматах (в)

В електричній наносхемі суматора на КА (рис.6.7, в) показано приклад додавання згідно з рівняннями (6.4) та (6.5) і умовами електричної індукції в комірках КА двох доданків 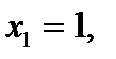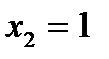і числа переносу з молодшого розряду 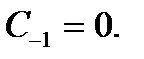Отримуємо, вочевидь, 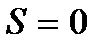та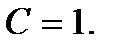

Для реалізації RS – тригера на КА існує декілька варіантів з’єднання логічних елементів, два з яких показані на рис.6.8. Це, по-перше, – на двох однакових схемах 2АБО-НІ (а), і, по-друге, – на інверторі DD1 та УМЕ DD2 (б).

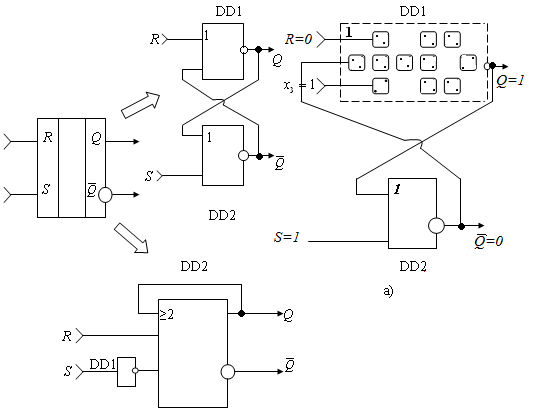
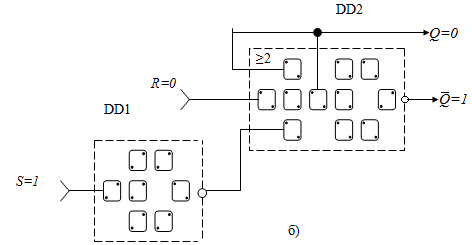
Рис.6.8. Схеми RS-тригера на КА

Коли на настановних входах R і S у двох схемних реалізаціях RS-триггера на КА (рис.6.8) діють різні сигнали, то в першому варіанті (а) тригер знаходиться у стані установки ( 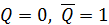), а друга схема (б) – у скинутому стані ( ).

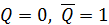Демультиплексор розподіляє вхідну інформацію, отриману з одного каналу 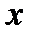, поміж декількома виводами 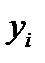. Наприклад, на рис 6.9 наведена логічна наносхема демультиплексора, побудована на одному інверторі DD1 та двох елементах 2І DD2 й DD3 (б), а також його електрична схема на КА (в).

г)

Рис.6.9. Демультиплексор (1→2): умовне позначення (а), реалізації на логічних елементах (б) та на КА (в) і таблиця станів (г)

Логіка функціонування демультиплексора (1→2) описується наступними рівняннями:

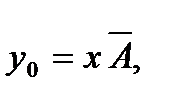(6.6)

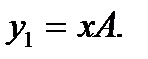(6.7)

Цим рівнянням відповідає спрощена таблиця дійсності:

х	А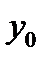
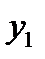
	х	––
	––	х

Вона показує, що стан на вході 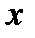передається на вихід 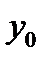тільки тоді, коли на адресному вході діє нуль 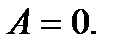В протилежній ситуації 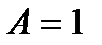інформаційний вхід 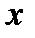підключається до виходу .

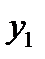Таким чином, квантові автомати мають просту коміркову структуру і дозволяють проектувати уніфіковані найпростіші пристрої цифрової та логічної наноелектроніки.