Деление чисел в машинах с плавающей запятой.

ДЕЛЕНИЕ ЧИСЕЛ В ДОПОЛНИТЕЛЬНОМ КОДЕ.

Различают схемы деления с восстановлением остатка и без восстановления остатка. Операцию деления выполняют с помощью операций сдвига и сложения на сумматорах дополнительного кода.

Операцию деления без восстановления остатка выполняют по следующей схеме:

1. Уравнивают разрядную сетку делимого и делителя.

2 Если делимое А>0, то А =А-В. Если полученная разность А>0, то увеличить на единицу значение целой части частного C и перейти к пункту 3, иначе закончить формирование целой части частного и перейти к пункту 4.

3 Пункт 2 повторить до тех пор, пока полученная разность A не станет меньше 0.

4 Выполнить линейный сдвиг А на один разряд влево.

5 Если A>0, то найти А=А-B, иначе А=А+В.

6 Если A>0, то i – му разряду дробной части присвоить 1, иначе 0.

7 Если число знаков после запятой меньше необходимого, то вернуться к пункту 4.

Пример: А=10, В=3 [А]дк= 00 1010 [В]дк=00 0011 [-В]дк=11 1101

00 1010

11 1101

000111 >0 inc ( c )

00 0111

11 1101

00 0100 >0 inc ( c )

00 1000

11 1101

00 0001 >0 inc (c )

00 0001

11 1101

11 1110 <0 “,”

сдвиг 11 1100 11 1100

00 0011

11 1111 <0 011,0

сдвиг 11 1110 11 1110

00 0011

00 0001 >0 011,01

сдвиг 00 0010 00 0010

11 1101

11 1111 <0 011,010 ….

Операцию деления c восстановлением остатка выполняют по следующей схеме:

1. Уравнивают разрядную сетку делимого и делителя.

2. Если делимое А>0, то А =А-В. Если полученная разность А>0, то увеличить на единицу значение целой части частного C и перейти к пункту 3, иначе закончить формирование целой части частного и перейти к пункту 4.

3. Пункт 1 повторить до тех пор, пока полученная разность A не станет меньше 0.

4. Выполнить восстановление остатка А=А+В.

5. Выполнить линейный сдвиг А на одну позицию влево.

6. Найти А=А-В.

7. Если А<0, то то i – му разряду дробной части присвоить 0 и выполнить восстановление А=А+В, иначе i – му разряду дробной части присвоить 1.

8. Если число знаков после запятой меньше необходимого, то вернуться к пункту 5.

Пример А=12 В=5 [А]дк= 00 1100 [В]дк=00 0101 [-В]дк=11 1011

00 1100

11 1011

00 0111 >0 inc( c) 001

00 0111

11 1011 >0 inc( c) 010

00 0010

00 0010

11 1011

11 1101 <0 010,

восстановление 11 1101+ 00 0101= 00 0010

сдвиг 00 0100

00 0100+ 11 1011= 11 1111 <0 010 ,0

сдвиг 11 1110

восстановление 11 1111+ 00 0101= 00 0011

сдвиг 00 0110

00 0110+11 1011= 00 0001 >0 010,01…

Деление чисел в машинах с плавающей запятой.

Деление двоичных чисел, представленных в форме с плавающей запятой.

При операции деления чисел, представленных в форме с плавающей запятой их мантиссы делятся, как числа с фиксированной запятой, а порядки вычитываются. В обоих случаях проверка на переполнение обязательна. Но, т.к. реально вычитываются характеристики чисел, то деление выполняется по следующей формуле:

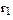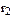A1 : A2 = m12 : m22 = (m1 : m2)2 .

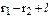Знак ответа определяется обычным образом. Если ответ получился ненормализованный, то выполняется процедура нормализации и округления ответа.

Т.к. мантиссы операндов нормализованы, то возможны случаи, когда

|mA| |mB|; |mA| < |mB|. В первом случае перед началом деления надо вычесть делитель из делимого и в целую часть мантиссы частного записать 1. Затем продолжать делить числа обычным методом. После получения частного очевидно, что оно не будет нормализованным. Значит надо нормализовать частное, т.е. в данном случае сдвинуть его на 1 разряд вправо, а к порядку частного добавить 1.

Напомним, что при реализации алгоритмов математических операций в формате с плавающей запятой каждый раз, когда осуществляется та или иная процедура, затрагивающая характеристики операндов или результата, производится контроль над переполнением и исчезновением порядка, т.е. контролируется условие

0 r rmax ,

где rmax = l + pmax .

Рассмотрим пример:

A = 10 = 0,1010, pA = 4, B = 2 = 0,1, pB = 2. p = pA - pB = 2. mA = 0.1010,

mB = 0.1 , (mB)l = 1.1000. |mA| > |mB|. При первом вычитании mB из mA 1 записываем в целую часть частного:

0.1010

+ 1.1000

а0 0.0010 С = 1,XX, далее, будем делить методом деления без восстановления остатка.

2а0 0.0100

+ 1.1000

а1 1.1100 а1<0 С = 1,0

2a1 1.1000

+ 0.1000

0.0000 a2 = 0 С = 1,01, сдвигаем вправо С = 0,101, p = p + 1 = 3.

В завершение обзора принципов организации арифметических действий с двоичными числами нужно отметить, что в Главе 11 подробно рассмотрены все алгоритмы арифметических процедур с числами в формах с фиксированной и плавающей запятой.

1. Записываем делимое А и делитель В в форме с плавающей точкой. Выравниваем мантиссы путем дописывания незначущих нулей справа.

2. Определяем знак частного путем сложения по модулю 2 знаковых цифр операндов.

3. Определяем порядок частного путем вычитания порядка делителя из порядка делимого

4. Если мантисса делимого больше мантиссы делителя, то вычитаем из мантиссы делимого мантиссу делителя в целую часть мантиссы частного записать 1, иначе записываем 0. Затем делим модули мантисс модули мантисс операндов по правилам деления чисел с фиксированной точкой.

5. Выполняем нормализацию мантиссы частного и ее округление.

6. Присваиваем знак мантиссе результата.